Prova in itinere 05/06

FACOLTÀ DI INGEGNERIA - SEDE DI MODENA
CORSO DI LAUREA IN INGEGNERIA MECCANICA
PROVA IN ITINERE DI ”MECCANICA RAZIONALE A”
- a.a. 2005/06, giovedi 10/11/2005 -
PROVA A
Domande di teoria
1) Formula fondamentale della cinematica rigida: a) scriverla; b) dire a che cosa serve; c)
dimostrarla (punti 7)
2) Forza peso:
a) di un punto; b) di un sistema di punti (punti 7)
3) Asse centrale di un sistema di forze:
a) in quali casi esiste?
b) definizioni (punti 3)
4) Centro di istantanea rotazione: a) definizione ed utilità; b) teoremi utili a determinarlo
per via geometrica (solo enunciati) (punti 3)
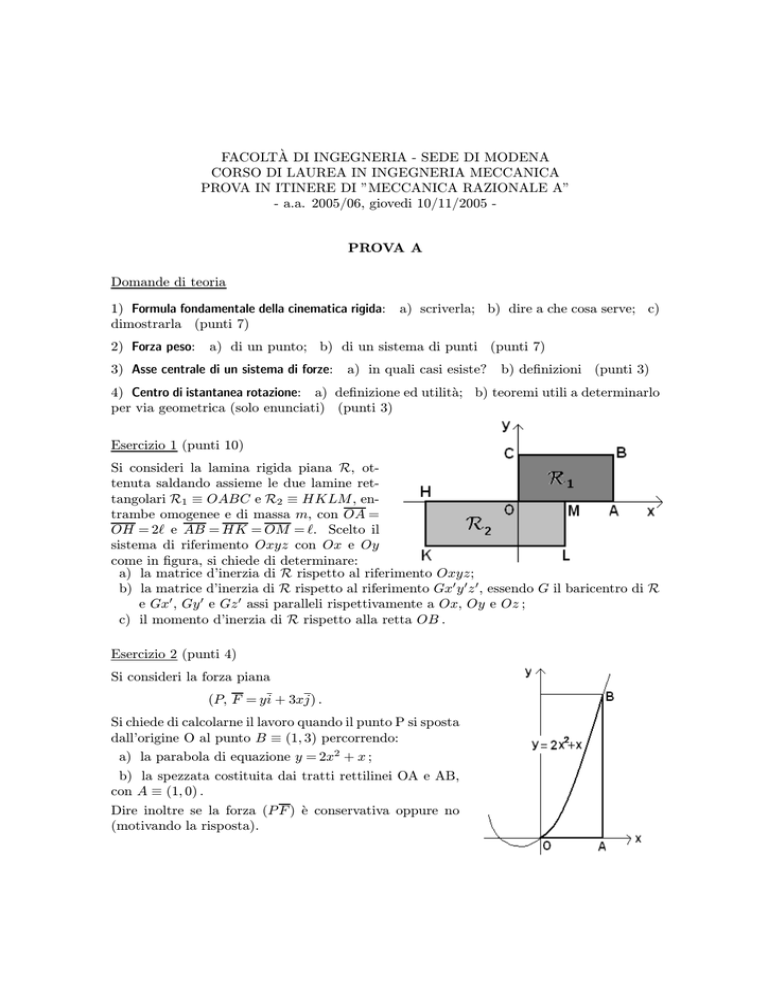
Esercizio 1 (punti 10)
Si consideri la lamina rigida piana R, ottenuta saldando assieme le due lamine rettangolari R1 ´ OABC e R2 ´ HKLM , entrambe omogenee e di massa m, con OA =
OH = 2ℓ e AB = HK = OM = ℓ. Scelto il
sistema di riferimento Oxyz con Ox e Oy
come in figura, si chiede di determinare:
a) la matrice d’inerzia di R rispetto al riferimento Oxyz;
b) la matrice d’inerzia di R rispetto al riferimento Gx′ y ′ z ′ , essendo G il baricentro di R
e Gx′ , Gy ′ e Gz ′ assi paralleli rispettivamente a Ox, Oy e Oz ;
c) il momento d’inerzia di R rispetto alla retta OB .
Esercizio 2 (punti 4)
Si consideri la forza piana
(P, F = yi + 3xj) .
Si chiede di calcolarne il lavoro quando il punto P si sposta
dall’origine O al punto B ´ (1, 3) percorrendo:
a) la parabola di equazione y = 2x2 + x ;
b) la spezzata costituita dai tratti rettilinei OA e AB,
con A ´ (1, 0) .
Dire inoltre se la forza (P F ) è conservativa oppure no
(motivando la risposta).
FACOLTÀ DI INGEGNERIA - SEDE DI MODENA
CORSO DI LAUREA IN INGEGNERIA MECCANICA
PROVA IN ITINERE DI ”MECCANICA RAZIONALE A”
- a.a. 2005/06, giovedi 10/11/2005 -
PROVA B
Domande di teoria
1) Teoremi di composizione delle velocità e delle accelerazioni: a) scrivere le formule che li
sintetizzano, spiegando quale problema risolvono e il significato di ciascun termine, dando
anche le espressioni utili ai fini del loro calcolo; b) dimostrare il teorema di composizione
delle velocità; (punti 7)
2) Definizione di lavoro infinitesimo per un sistema di forze e sua espressione nel caso che le
forze siano applicate ad un corpo rigido; (punti 6)
3) Cos’è la risultante di un sistema di forze? quando esiste? quali particolari sistemi di forze
conosci che ammettono la risultante? Il sistema costituito da due forze parallele ammette
la risultante? Se si, qual è? (punti 5)
4) Definizione di polo delle accelerazioni e sua utilità.
(punti 2)
Esercizio 1 (punti 10)
Si consideri la lamina rigida piana R, ottenuta saldando assieme le due lamine rettangolari R1 ´ HKLM
e R2 ´ OABM , entrambe omogenee e di massa m, con
OA = OH = 2ℓ e OM = HK = ℓ. Scelto il sistema di
riferimento Oxyz con Ox e Oy come in figura, si chiede
di determinare:
a) la matrice d’inerzia di R rispetto al riferimento
Oxyz;
b) la matrice d’inerzia di R rispetto al riferimento
Gx′ y ′ z ′ , essendo G il baricentro di R e Gx′ , Gy ′ e Gz ′
assi paralleli rispettivamente a Ox, Oy e Oz ;
c) il momento d’inerzia di R rispetto alla retta OK .
Esercizio 2 (punti 4)
Si consideri la forza piana
(P, F = 2 y i + x j) .
Si chiede di calcolarne il lavoro quando il punto P si sposta
dall’origine O al punto B ´ (1, 3) percorrendo:
a) la parabola di equazione y = x2 + 2x ;
b) la spezzata costituita dai tratti rettilinei OA e AB,
con A ´ (0, 3) .
Dire inoltre se la forza (P F ) è conservativa oppure no
(motivando la risposta).
SVOLGIMENTO DEGLI ESERCIZI
DELLA PROVA IN ITINERE DI ”MECCANICA RAZIONALE A”
- a.a. 2005/06, giovedi 10/11/2005 -
PROVA A
Esercizio 1 (punti 10)
Si consideri la lamina rigida piana R, ottenuta saldando assieme le due lamine rettangolari R1 ´ OABC e R2 ´ HKLM , entrambe omogenee e di massa m, con OA =
OH = 2ℓ e AB = HK = OM = ℓ. Scelto il
sistema di riferimento Oxyz con Ox e Oy
come in figura, si chiede di determinare:
a) la matrice d’inerzia di R rispetto al riferimento Oxyz;
b) la matrice d’inerzia di R rispetto al riferimento Gx′ y ′ z ′ , essendo G il baricentro di R
e Gx′ , Gy ′ e Gz ′ assi paralleli rispettivamente a Ox, Oy e Oz ;
c) il momento d’inerzia di R rispetto alla retta OB .
Svolgimento
a) Osserviamo innanzitutto che i baricentri G1 della lamina R1 , G2 della lamina R2 e G
dell’intera lamina sono i seguenti:
G1 ´ ℓ, 2ℓ ,
G2 ´ ¡ 2ℓ , ¡ 2ℓ ,
G ´ 4ℓ , 0 .
Utilizzando ora i risultati visti sulle lamine rettangolari omogenee, il teorema di Huyghens e
il teorema sulla trasposione dei momenti di deviazione, tenendo anche conto che i momenti
di deviazione B ′ e C ′ sono nulli, si ha:

AO (R1 ) = 13 mℓ2



 B (R ) = 1 m(2ℓ)2 = 4 mℓ2
O
1
3
3

CO (R1 ) = AO (R1 ) + BO (R1 ) = 53 mℓ2


 ′
AO (R1 ) = 14 m(2ℓ)ℓ = 12 mℓ2
Si ha quindi
 2
mℓ2
 3
3
JO = 
 ¡ mℓ2
4
0

AO (R2 ) = 13 mℓ2



2

1
BO (R2 ) = 12
m(3ℓ)2 + m ℓ4 = mℓ2

CO (R2 ) = AO (R2 ) + BO (R2 ) = 43 mℓ2


 ′
AO (R2 ) = m xG2 yG2 = 14 mℓ2 .
3
¡ mℓ2
4
7 2
mℓ
3
0
0
0
3mℓ2


.

b) Utilizzando ancora il teorema di Huyghens e il teorema sulla trasposione dei momenti
di deviazione, e tenendo conto gli assi Ox e Gx′ coincidono, si ha:

AG (R) = AO (R) = 23 mℓ2



2

BG (R) = BO (R) ¡ (2m) 4ℓ = 53
mℓ2
24
2

CG (R) = AG (R) + BG (R) = 23

8 mℓ

 ′
AG (R) = A′O (R) ¡ (2m)xG yG = 34 mℓ2
c) La retta OB ha equazione y =
=)
 2
mℓ2
 3
 3
2
JG = 
 ¡ 4 mℓ

0
x
. Di conseguenza:
2
α=
√2
5
,
3
¡ mℓ2
4
53 2
mℓ
24
0
β=
√1
5
0
0
23 2
mℓ
8



.


γ = 0.
,
Si ha quindi
IOB = AO (R) α2 + BO (R) β 2 ¡2A′O (R) αβ =
2 4 7 1
1 2
3 2
¢ + ¢ ¡2 ¢ ¢ p ¢ p mℓ2 = mℓ2 .
3 5 3 5
4
5
5
5
Esercizio 2 (punti 4)
Si consideri la forza piana
(P, F = yi + 3xj) .
Si chiede di calcolarne il lavoro quando il punto P si sposta
dall’origine O al punto B ´ (1, 3) percorrendo:
a) la parabola di equazione y = 2x2 + x ;
b) la spezzata costituita dai tratti rettilinei OA e AB,
con A ´ (1, 0) .
Dire inoltre se la forza (P F ) è conservativa oppure no
(motivando la risposta).
Svolgimento
Innanzitutto si ha:
dL = F ¢ dP = (y i + 3x j) ¢ (dx i + dy j) = y dx + 3x dy .
a) Essendo y = 2x2 + x l’equazione della traiettoria, si ha dy = (4 x + 1) dx . Il lavoro
La della forza quando P percorre il tratto di parabola è dunque il seguente:
La =
=
B
dL =
O
1
0
B
(y dx + 3x dy) =
O
0
1
(2x2 + x)dx + 3x(4x + 1)dx =
x3 1
x2 1 14
20
(14 x2 + 4 x) dx = 14
+4
=
+2=
.
3 0
2 0
3
3
b) Osserviamo che lungo il tratto OA si ha y = 0 e dy = 0 , mentre lungo il tratto
AB si ha x = 1 e dx = 0 . Da ciò consegue che
Lb =
B
O
dL =
A
O
dL +
B
A
dL =
0
1
(0 ¢ dx + 3x ¢ 0) +
0
3
(y ¢ 0 + 3 ¢ 1 ¢ dy) =
0
3
3 dy = 9 .
PROVA B
Esercizio 1
Si consideri la lamina rigida piana R, ottenuta saldando assieme le due lamine rettangolari R1 ´
HKLM e R2 ´ OABM , entrambe omogenee e
di massa m, con OA = OH = 2ℓ e OM = HK = ℓ.
Scelto il sistema di riferimento Oxyz con Ox e Oy
come in figura, si chiede di determinare:
a) la matrice d’inerzia di R rispetto al riferimento Oxyz;
b) la matrice d’inerzia di R rispetto al riferimento Gx′ y ′ z ′ , essendo G il baricentro di R
e Gx′ , Gy ′ e Gz ′ assi paralleli rispettivamente a Ox, Oy e Oz ;
c) il momento d’inerzia di R rispetto alla retta OK .
Svolgimento
a) Osserviamo innanzitutto che i baricentri G1 della lamina R1 , G2 della lamina R2 e G
dell’intera lamina sono i seguenti:
G2 ´ ¡ 2ℓ , ¡ℓ ,
G1 ´ 2ℓ , 2ℓ ,
G ´ 0, ¡ 4ℓ .
Utilizzando ora i risultati visti sulle lamine rettangolari omogenee, il teorema di Huyghens
e il teorema sulla trasposione dei momenti di deviazione, tenendo anche conto del fatto
che i momenti di deviazione B ′ e C ′ sono nulli, si ha:

AO (R1 ) = 13 mℓ2



2

1
BO (R1 ) = 12
m (3ℓ)2 + m 2ℓ = mℓ2

C (R ) = AO (R1 ) + BO (R1 ) = 43 mℓ2


 O′ 1
AO (R1 ) = m xG1 yG1 = 14 mℓ2 .
Si ha quindi
 5
mℓ2
3

3
JO = 
 ¡ mℓ2
4
0

AO (R2 ) = 13 m(2ℓ)2 = 43 mℓ2



 B (R ) = 1 mℓ2
O
2
3

CO (R2 ) = AO (R2 ) + BO (R2 ) = 53 mℓ2


 ′
AO (R2 ) = m xG2 yG2 = 12 mℓ2
3
¡ mℓ2
4
4 2
mℓ
3
0
0
0
3mℓ2


.

b) Utilizzando ancora il teorema di Huyghens e il teorema sulla trasposione dei momenti
di deviazione, e tenendo conto gli assi Oy e Gy′ coincidono, si ha:
2

2
AG (R) = AO (R) ¡ (2m) 4ℓ = 37

24 mℓ



BG (R) = BO (R) = 43 mℓ2
 CG (R) = AG (R) + BG (R) = 23 mℓ2

8

 ′
AG (R) = A′O (R) ¡ (2m)xG yG = 34 mℓ2
=)
 37
mℓ2
 24
 3
2
JG = 
 ¡ 4 mℓ

0
3
¡ mℓ2
4
4 2
mℓ
3
0
0
0
23 2
mℓ
8



.


c) La retta OB ha equazione y =
Si ha quindi
x
. Di conseguenza:
2
IOB = AO (R) α2 + BO (R) β 2 ¡ 2A′O (R) αβ =
α=
√2
5
,
β=
√1
5
γ = 0.
,
5 4 4 1
3 2
1 ¢ + ¢ ¡ 2 ¢ ¢ p ¢ p mℓ2 = mℓ2 .
3 5 3 5
4
5
5
Esercizio 2
Si consideri la forza piana
(P, F = 2 y i + x j) .
Si chiede di calcolarne il lavoro quando il punto P si sposta
dall’origine O al punto B ´ (1, 3) percorrendo:
a) la parabola di equazione y = x2 + 2x ;
b) la spezzata costituita dai tratti rettilinei OA e AB,
con A ´ (0, 3) .
Dire inoltre se la forza (P F ) è conservativa oppure no
(motivando la risposta).
Svolgimento
Innanzitutto si ha:
dL = F ¢ dP = (2y i + x j) ¢ (dx i + dy j) = 2y dx + x dy .
a) Essendo y = x2 + 2x l’equazione della traiettoria, si ha dy = (2 x + 2) dx . Il lavoro
La della forza quando P percorre il tratto di parabola è dunque il seguente:
La =
=
B
dL =
O
1
0
B
(2y dx + x dy) =
O
0
1
2(x2 + 2x) + x(2x + 2) dx =
x3 1
x2 1
4 6
13
(4 x2 + 6 x) dx = 4
+6
= + =
.
3 0
2 0
3 2
3
b) Osserviamo che lungo il tratto OA si ha x = 0 e dx = 0 , mentre lungo il tratto
AB si ha y = 3 e dy = 0 . Da ciò consegue che
Lb =
B
O
dL =
A
O
dL +
B
A
dL =
0
3
(2y ¢ 0 + 0 ¢ dy)+
0
1
(2¢ 3dx+ x ¢0 dy) =
0
1
6 dx = 6 .