Correnti elettriche, resistenze, legge di Ohm
Se in un conduttore, tra due punti qualsiasi sulla sua superficie o al suo
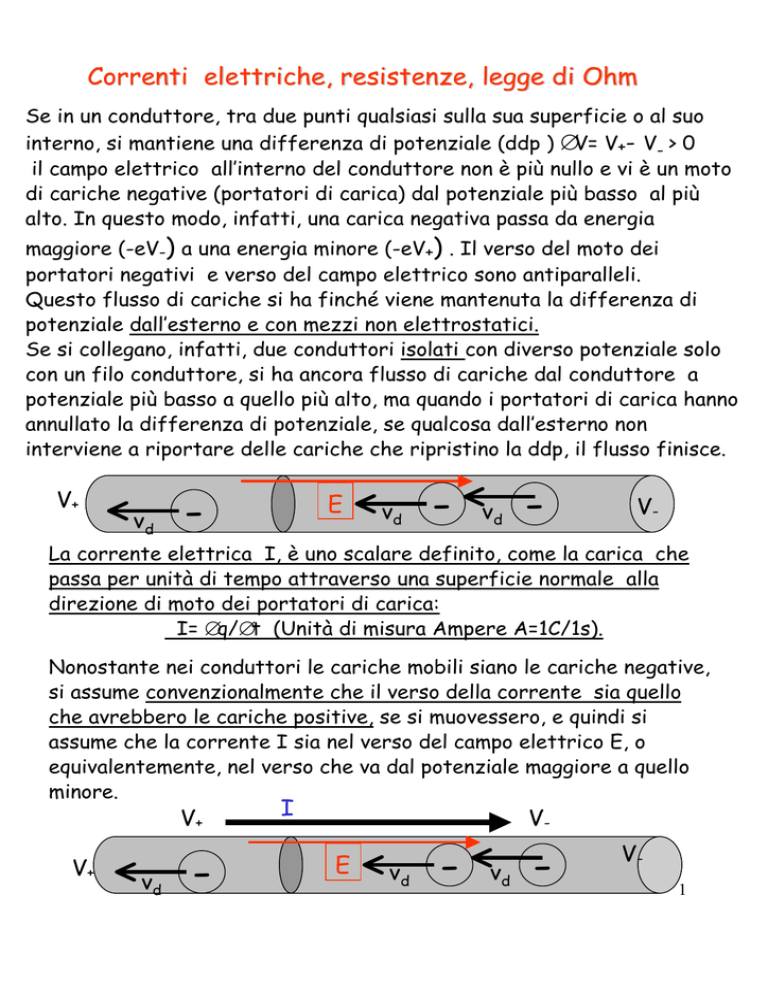
interno, si mantiene una differenza di potenziale (ddp ) ∆V= V+- V- > 0
il campo elettrico all’interno del conduttore non è più nullo e vi è un moto
di cariche negative (portatori di carica) dal potenziale più basso al più
alto. In questo modo, infatti, una carica negativa passa da energia
maggiore (-eV-) a una energia minore (-eV+) . Il verso del moto dei
portatori negativi e verso del campo elettrico sono antiparalleli.
Questo flusso di cariche si ha finché viene mantenuta la differenza di
potenziale dall’esterno e con mezzi non elettrostatici.
Se si collegano, infatti, due conduttori isolati con diverso potenziale solo
con un filo conduttore, si ha ancora flusso di cariche dal conduttore a
potenziale più basso a quello più alto, ma quando i portatori di carica hanno
annullato la differenza di potenziale, se qualcosa dall’esterno non
interviene a riportare delle cariche che ripristino la ddp, il flusso finisce.
V+
vd
-
E
vd
-
vd
-
V-
La corrente elettrica I, è uno scalare definito, come la carica che
passa per unità di tempo attraverso una superficie normale alla
direzione di moto dei portatori di carica:
I= ∆q/∆t (Unità di misura Ampere A=1C/1s).
Nonostante nei conduttori le cariche mobili siano le cariche negative,
si assume convenzionalmente che il verso della corrente sia quello
che avrebbero le cariche positive, se si muovessero, e quindi si
assume che la corrente I sia nel verso del campo elettrico E, o
equivalentemente, nel verso che va dal potenziale maggiore a quello
minore.
V+
V+
vd
-
I
V-
E
vd
-
vd
-
V1
-Si definisce il vettore densità di corrente j come la corrente che
passa per unità di tempo e di superficie attraverso una superficie
A(sezione del conduttore) perpendicolare alla direzione della
velocità dei portatori di carica positivi (per la convenzione detta).
Il vettore j ha direzione e verso del campo elettrico (per la
convenzione detta)
j=
1 dQ
A dt
-Poiché i portatori di carica sono accelerati dal campo elettrico e
allo stesso tempo frenati dagli urti con gli altri portatori di cariche
e dalle interazioni con gli atomi, l’effetto totale è che si muovono
(ed è verificato sperimentalmente) con una velocità costante.
- Questa velocità viene chiamata velocità di deriva vd (o velocità
limite come nel moto di un oggetto in un fluido viscoso)
-Se n=N/∆V è il numero di portatori di carica, ognuno con carica q,
che si muovono con velocità di deriva vd in un volume ∆V del
conduttore ( vedi figura: il volume ha base la sezione A del
conduttore e altezza dl=vddt, per cui ∆V=A vddt), allora la carica
totale che in un tempo dt attraversa il volume è dQ=Nq=(n/∆V )q.
Quindi da :
j=
1 dQ
A dt
si ottiene j = nqvd (unità di misura A/m2) e
I = Ç j·dA=(j A, se j uniforme sulla area A e A normale a j) : l’intensità
di corrente è il flusso attraverso A della densità j.
∆V=A vddt
V+
+
vd
E
A
+
vd
dl= vddt
A
+v
d
V2
Nei sistemi fluidi o ionizzati in cui le cariche sia positive che negative
possono muoversi, la densità di corrente di carica positiva j+ =n+ q+ v+d e
quella negativa j-= n- q- v-d. sono nella stessa direzione e verso.
Infatti la velocità di deriva delle cariche negative è direzione opposta a
quella degli ioni positivi, ma anche la carica q- è negativa e quindi il
prodotto j- =n-(-q+)(-v-d)= n- q+ v+d, quindi
j = j+ + j- =(n+ + n-) q+ v+d
n+ e n- sono il numero di portatori di carica positiva e negativa per unità
di volume.
3
Resistenza elettrica
La corrente che circola in un conduttore, a parità di ddp ∆V applicata,
dipende dalla struttura atomica,dal numero dei portatori di carica, e
dall’impedimento che essi trovano a muoversi: tutto ciò si traduce in una
caratteristica del conduttore chiamata resistenza del conduttore, che è
una caratteristica del tipo di materiale di cui è composto il conduttore.
In alcuni conduttori, detti ohmici, si verifica che la resistenza R è
sempre la stessa qualunque sia la ∆V applicata, ovvero, aumentando o
diminuendo ∆V, la corrente I che fluisce nel conduttore aumenta e
diminuisce in modo proporzionale. Quindi il rapporto I/∆V è costante.
La resistenza per ogni sostanza ohmica è definita dal rapporto:
R=
∆V
I
(Ω (Ohm)=1V/1A)
Il valore della resistenza, costante per un conduttore ohmico, varia al
variare del conduttore ( la resistenza dell’argento diverso dalla
resitenza del rame, del nichel…)
Da questa definizione segue quella che viene chiamata la I legge di Ohm;
legge empirica che vale per molti conduttori ohmici
∆V =RI
ovvero la caduta di potenziale ai capi di una resistenza ohmica è data dal
prodotto della resistenza R per la corrente I, con R proprietà del
conduttore considerato, indipendente sia dalla ddp che dalla corrente.
∆V(V)
Cond. B
∆V(V)
Cond. A
I(A)
Curve caratteristiche per
cond. ohmici
I(A)
Curva caratteristica per
cond. non ohmico
La resistenza si definisce anche per i conduttori non ohmici, ma non vale
la legge di Ohm e la resistenza R è ancora una proprietà del conduttore
considerato, ma dipende sia dalla ddp che dalla corrente e con esse
4
varia (vedi grafico a destra, la resistenza ∆V/I varia al variare della
corrente)
Resistenza elettrica e resistività
La resistenza dipende dalla forma geometrica del conduttore e dalle sue
dimensioni e dal materiale: la dipendenza del materiale è la proprietà che
si chiama resistività, indicata con ρ (da non confondere con la densità
volumetrica di carica elettrica). σ= 1/ρ è chiamata conduttività elettrica
del conduttore.
Relazione tra resistenza e resistività e forma del conduttore.
Conduttore omogeneo isotropo (stesso materiale con le stesse
caratteristiche in tutte le direzioni) a sezione S costante.
L
V+
V- S
E
∆V
Nel conduttore omogeneo isotropo a sezione S costante, lungo L, ai cui
capi vi sia una ddp ∆V, il campo elettrico è per ragioni di simmetria
uniforme e così
la densità di corrente che circola:
Quindi ∆V=EL e j=IS, e ne segue che
∆V EL
R=
=
I
jS
La resistività ρ del materiale è la costante di proporzionalità tra il campo
elettrico E e la densità di corrente j
r
r
E
ρ = ⇒ j = σE
j
Analogamente la conduttività σ è la costante di proporzionalità tra j e E:
j= σ E è la relazione è conosciuta come la legge microscopica di Ohm,(o
relazione “costitutiva” in conduttori ohmici)
La relazione che lega la resistenza alle caratteristiche del conduttore è
per il conduttore a sezione costante
∆V
L
R=
=ρ
I
S
Maggiore la lunghezza del conduttore è maggiore la resistenza, maggiore
5
la sezione, minore la resistenza.
Resistenza elettrica: resistività 2
La resistività si misura in Ω⋅m, l’unità di misura della conduttività σ viene
indicata con mho=(Ω⋅m)-1 (o Siemens⋅ m).
I valori di resistività variano di vari ordini di grandezza: dai 10-8 Ω⋅m
(argento, rame e metalli) a 1011 Ω⋅m nelle sostanze che possono essere
considerati isolanti (quarzo,legno).
Nelle rocce vi è una ampia variabilità, e il valore dipende fortemente dalla
componente in metalli, dalla presenza di acqua, di pori, saturati in fluidi,
dalla presenza di argille ecc.
In particolare sia le rocce della litosfera che del mantello hanno un
comportamento particolare, chiamato comportamento semiconduttore
(tipico di materiali che contengono silicio e germanio).
I semiconduttori hanno una struttura atomica particolare, in cui esiste
un gap di energia tra l’ultima orbita parzialmente riempita e la successiva
L’energia termica in questo caso aiuta a superare il gap d’energia che non
consentirebbe il fluire della corrente. Questi sistemi hanno un
comportamento isolante a temperatura ambiente, mentre la loro
resistività diminuisce quando aumenta la temperatura, secondo una legge
esponenziale decrescente
−β (T −T0 )
ρ = ρoe
con ρ0 resistività a temperatura ambiente T0 [in gradi Kelvin]. Ovviamente
la loro conduttività aumenta con la temperatura che cresce.
Nei metalli puri, al contrario, la resistività aumenta quando aumenta la
temperatura (aumenta l’agitazione termica e aumentano gli urti) secondo
una legge lineare:
ρ = ρ o (1 + α(T − T0 ))
dove l’ordine di grandezza del coefficiente α [K-1] è 10-3.
Un comportamento anomalo hanno alcuni metalli e composti particolari,
isolanti a temperatura ambiente, ma nei quali la resistività sparisce a
temperature vicino allo zero assoluto: materiali superconduttori. 6
Legge dei nodi e Resistenze in serie e in parallelo
Il comportamento di diversi materiali conduttivi a contatto, con diverse
resistenze, è regolato dalla legge di Ohm e dalla legge di conservazione
della carica. La legge di conservazione della carica, in condizioni
stazionarie, dice che la carica che circola in condizioni stazionarie (non
dipendente dal tempo) in un circuito non può né essere creata né essere
persa. La legge di conservazione della carica è analoga per la circolazione
di corrente elettrica alla legge di conservazione della massa nei fluidi in
moto stazionario. Qui si esprime dicendo che I1=j1S1 è la corrente che
circola in un conduttore con sezione S1 e se questo conduttore si allarga a
diversa sezione mantenendo le stesse caratteristiche materiali allora la
corrente I2=j2S2=I1 , ovvero la densità deve cambiare, ma la quantità
totale di carica per unità di tempo non cambia.
Ancora, se un conduttore in cui circola una corrente I si divide per es. in
due conduttori,( che possono essere sia dello stesso materiale del
conduttore principale, ma anche di materiali diversi rispetto al primo e
tra loro), la somma delle correnti che fluisce nei due conduttori “a valle”
deve essere uguale alla corrente I che circola nel conduttore a monte: il
punto di divisione si chiama nodo e nel nodo la somma delle correnti
entranti deve essere uguali alla somma delle correnti che escono (LEGGE
DEI NODI):
I = I1 + I2
I=jS
I1=j1S1
I2 =j2S2
7
I = I1 + I2
La legge di nodi può ovviamente essere generalizzata a un numero
qualsiasi di correnti a valle e di correnti a monte:la somma delle
correnti entranti Iin deve essere uguale alla somma delle correnti
uscenti Iout .
Σ Iin = Σ Iout
Se si da valore positivo alle correnti che escono dalla superficie e
negativo a quelle che entrano, la legge dei nodi si esprime dicendo che
la somma algebrica di tutte le correnti deve essere nulla in un nodo.
I1
I2
I5
I3
I4
I1 + I3 = I2 + I4 + I5
R1
I1=j1S1
I=jS
VA
VB
I2 =j2S2
-I1 + I2- I3 + I4 + I5=0
I=jS
I
I1
VA
I2
I
R2
VB
- Nel sistema di figura, un filo di rame, per es., di sezione S, si divide in
due tronchi, chiamati “rami”.
-A parità di lunghezza e resistività, nei due rami si ha diversa
resistenza, visto che essi hanno sezione diverse dal ramo principale.
- Al nodo A il potenziale VA è uguale sia per il ramo principale che per i
due rami e al nodo B analogamente il potenziale VB è uguale per tutte
tre le componenti. Lo stesso vale se i due rami sono di materiale
conduttore.
- A destra è rappresentato schematicamente il sistema dei due rami,
con il simbolo che viene usato per la resistenza.
8
R1
I1=j1S1
I=jS
VA
VB
I=jS
I2 =j2S2
I
I1
VA
I2
I
R2
VB
- - Il sistema che è rappresentato è un sistema di resistenze in
parallelo: due o più resistenze i cui estremi hanno la stessa differenza
di potenziale.
- Anche in questo caso, come nei condensatori, si definisce un
componente equivalente che ha gli stessi effetti: la resistenza
equivalente.
La resistenza equivalente di due resistenze in parallelo è definita come
la resistenza che si trova alla stessa ddp ∆V=VA - VB e che è
attraversata dalla corrente totale. Quindi nell’esempio
Resistenza equivalente per resistenze in parallelo
Req =
∆V
∆V
=
I
I1 + I2
⇒
1
1
1
=
+
Req R1 R2
I + I2
I
I
1
1
1
= 1
= 1 + 2 =
+
Req
∆V
∆V ∆V R1 R2
⇒R
eq
=
R1R2
R1 + R 2
-Se le resistenze sono in parallelo, la resistenza equivalente è minore di
ciascuna delle due resistenze.
-Un parallelo viene utilizzato se si vuole che
- una resistenza debba essere attraversata da corrente minore di
quella fornita a valle, (partitore di corrente),
- o quando attraverso la misura della corrente che circola, conoscendo la
resistenza, si voglia misurare la ddp ai capi di una altra resistenza.
(voltmetro). Il voltmetro viene in parallelo in un circuito, cosi da avere e
misurare la stessa ddp della resistenza, e deve avere una grossa
resistenza, in modo da convogliare nello strumento la minore corrente
possibile, per non alterare la corrente nel circuito principale e quindi la
caduta di potenziale ai capi di questa.
9
VA
VC
I=jS
Resistenze in serie
I=j1S1
VB
VA
R1
VC
R2
VB
I
I
- Una situazione diversa è quella in cui o il ramo si restringe ( o si
allarga), o la corrente incontra a monte un materiale diverso (anche
della stessa sezione). Ora si hanno due resistori in serie, e la corrente
che li attraversa per la conservazione della carica non può cambiare.
- La “caduta di potenziale” per ogni resistore è ora diversa e la somma
delle ddp ai capi dei due resistori, ∆V1 =VA – Vc e ∆V2=Vc - VB è la ddp
totale ∆V= ∆V1 +∆V2= VA - VB applicata all’intero sistema. Nel punto di
contatto tra i due resistori il potenziale è lo stesso, VC.
- A destra è rappresentato schematicamente il sistema di resistenze in
serie: due o più resistenze attraversate dalla stessa corrente I.
-La resistenza equivalente di due resistenze in serie è definita come la
resistenza attraversata dalla corrente comune e ai cui capi vi è una ddp
che è la somma delle singole differenze di potenziali.
- Quindi nell’esempio:
Req =
V − VC VC − VA
∆V ∆V1 + ∆V2 ∆V1 ∆V2
=
=
+
= A
+
I
I
I
I
I
I
⇒R
eq
= R1 + R2 (res. in serie)
Se le resistenze sono in serie, la resistenza equivalente è maggiore di
di ciascuna delle due resistenze.
Una serie viene utilizzata
-se si vuole ripartire una ddp totale (partitore di potenziale)
- per misurare la corrente che circola in un circuito elettrico il
sistema di misura (amperometro) deve essere messo in serie alle
resistenze del circuito. Notare comunque che la corrente misurata
non è, a parità di ddp del generatore di corrente, la corrente che
circolerebbe nel circuito senza l’amperometro. Infatti se I=∆V/R è la
corrente che circola in un circuito con resistenza R alimentato a ∆V,
se Ra è la resistenza dell’amperometro in serie, la corrente che
circola e viene misurata è I=∆V/(R+ Ra). Minore è la resistenza
dell’amperometro maggiore l’accuratezza della misura.
10
Forza elettromotrice, potenza erogata e dissipata.
- Il sistema che fornisce la differenza di potenziale e che la mantiene
nonostante la circolazione di cariche è chiamato “forza elettromotrice”
e non può essere fornito da distribuzioni di cariche che creano campi
elettrostatici: il campo elettrostatico è conservativo e se un sistema di
resistenze viene collegato a un sistema statico, tutto il sistema si porta
in equilibrio, il potenziale diventa uguale su tutti i componenti e non
circola più corrente.
-Per ottenere una ddp stabile ai capi di un sistema di resistori serve un
sistema che mantenga la differenza di potenziale e continui a far
muovere le cariche a spese di qualche altra forma di energia.
La batteria o la pila, i generatori di correnti alternata, le celle solari
sono sistemi di questo tipo.
Per ognuna di esse si sfrutta un’altra forma di energia (chimica,
radiazione elettromagnetica, energia meccanica) per produrre energia
elettrica. Non entreremo in dettaglio sul funzionamento di questi
sistemi.
-La forza elettromotrice (fem) è la differenza di potenziale ai capi di
ognuno di questi dispositivi, che viene misurata quando ai suoi capi non vi
è nessuna resistenza di carico ( si dice a circuito aperto,ovvero
collegando il voltmetro direttamente a quelli che si chiamano poli
(positivo e negativo))della fem. Convenzionalmente al polo negativo si
assegna valore V=0 e la ddp misurata viene attribuita come potenziale
del polo positivo. Il simbolo della fem per circuiti in corrente continua
(non alternata) è:
+
I
V
-
f (fem) [Volt]
A circuito aperto fem=V
Interruttore aperto
11
f (fem) [Volt]
r
+
I
R
-
Interruttore chiuso
-Quando si chiude l’interruttore, la corrente circola dal polo positivo
attraverso la “resistenza di carico R” fino al polo negativo, e continua a
circolare nella fem dal polo negativo al polo positivo (e questo movimento
interno è avviene a spese della energia chimica, o meccanica ecc).
- Nel movimento all’interno della fem le cariche incontrano una
resistenza, propria di ogni dispositivo, chiamata resistenza interna
della fem (r), di solito molto minore della resistenza di carico R. La
resistenza interna viene di solito rappresentata all’esterno della fem
come resistenza aggiuntiva in serie a R.
La corrente che circola nel circuito rappresentato è quindi:
f
Legge di Ohm generalizzata
I=
R+r
-Ne consegue che quando il circuito è chiuso, la fem fornisce sia la ddp
ai capi della resistenza ∆VR=RI, ma anche la ddp per far fluire la
corrente al suo interno ∆vi=Ir. Quindi a circuito chiuso f= ∆VR + ∆vi.
-Un voltmetro collegato alla fem (in parallelo con la fem e con la
resistenza di carico R), a circuito chiuso, misura la ddp ∆Vf=f-Ir. La
ddp di funzionamento nel circuitp è minore di quella dichiarata sul
generatore e varia con la resistenza interna del generatore.
- Passando dal polo negativo al positivo si ha un salto positivo della ddp,
se la corrente fluisce nel verso regolare da - a +, ma si deve notare che
la corrente in una batteria può fluire anche in senso contrario, e in
questo caso essa si sta caricando, ovvero assorbe energia., quando in una
fem la corrente circola nel senso dal positivo al negativo (ovviamente ci
sarà un’altra batteria a dare energia)allora la ddp ai suoi capi è -f
f
f2
r1 + 1 f1 − f2
- + r2
I=
R + r1 + r2
I
12
R
- Energia dissipata, energia erogata, Legge di Joule per i conduttori
-Quando la carica dq si muove nel tempo dt attraverso la differenza di
potenziale ∆VR=(VA -VB)>0 ai capi di una resistenza R, si ha una perdita
di energia potenziale elettrica
−∆U=U(B)-U(A)=dq(VB- Va)=-dq ∆VR
I
VB<VA
VA
- Si definisce POTENZA DISSIPATA nella resistenza R la rapidità con
cui si perde energia elettrica
Pd =-∆U/dt= (dq/dt) ∆VR=I ∆VR (J/s=W)
-Se la resistenza è ohmica,
∆VR =RI
e la potenza dissipata può essere scritta nella forma
Pd=RI2= (∆VR)2/I.
Questa energia in condizioni stazionarie viene trasformata in calore (la
resistenza si riscalda). Questo calore viene ceduto con continuità
all’ambiente esterno, se questo è a temperatura più bassa (legge di
Joule o riscaldamento ohmico) o viene trasformata (come in lampadine
incandescenti)in energia luminosa (radiazione elettromagnetica)
-L’energia dissipata per unità di tempo, è fornita dalla batteria, che
mantiene la ddp ai capi della resistenza. Per trovare la POTENZA
EROGATA, basta considerare la ddp ai capi della batteria a circuito
chiuso e moltiplicarlo per la corrente che circola:
Pe= ∆Vi (dq/dt)=(f-Ir)I=fI-rI2
fI è la POTENZA NOMINALE erogata dalla fem se in essa circola una
corrente I. Il termine - rI2 è la perdita di potenza dovuta alle
resistenze interne, la fem si riscalda durante l’uso. Normalmente
i generatori di fem aumentano la loro resistenza interna con l’uso.
13
Non verrano svolti in questo corso gli argomenti :
Leggi di Kirckhoff: per l’analisi dei circuiti più complessi di quelli
trattati in questa parte e la parte di carica e scarica di un sistema
conduttore come un condensatore. Si raccomanda di leggere gli
argomenti anche se non sono materia di esame, per avere una idea
quando argomenti attinenti verrano considerati nei corsi successivi.
14











