Corrente elettrica
Cariche in movimento e legge di Ohm
Conduttori, isolanti e
semiconduttori
Normalmente quasi tutti gli elettroni sono fortemente
legati ai loro nuclei eccetto quelli più esterni che
sono liberi di muoversi se sottoposti ad una piccola
fonte di energia (un incremento di temperatura o una
piccola ddp)
m
e 2 n
Negli isolanti non ci sono elettroni liberi e una grande ddp non riesce
spostare elettroni anche se può vincere la rigidità dielettrica.
I semiconduttori sono come gli isolanti, ma se opportunamente
drogati possono far passare corrente anche con una discreta ddp.
Nei conduttori il numero degli elettroni è grande e la corrente scorre
facilmente, ma all’aumentare della temperatura aumenta il numero
delle collisioni e conseguentemente la resistività aumenta.
Corrente elettrica
• Nei metalli ci sono elettroni che si muovono anche velocemente fra
un estremo e l’altro del metallo.
•Sono gli elettroni più esterni di ciascun atomo che sono debolmente
legati ai nuclei.
• Ma senza una differenza di potenziale agli estremi il moto è
totalmente casuale. Non c’è corrente.
• La corrente elettrica è il frutto di una differenza di potenziale
applicata agli estremi di un conduttore.
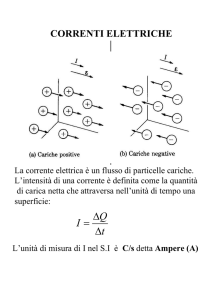
• La corrente è definita
come una quantità di
carica dq che nel tempo
dt passa nel conduttore.
i = dq/dt
+
_
Definizione di corrente
La quantità di carica che passa in un filo di sezione definita è data da:
q = ∫dq = ∫i dt
In regime stazionario, cioè se la corrente non varia nel tempo, in ogni
sezione di un conduttore tanti elettroni entrano e altrettanti ne escono
(conservazione della carica) 1A (ampere) = 1 C/s La corrente è uno
scalare
La densità di corrente J è il flusso di cariche che attraversano una
superficie A
J = i/A
Legge di Ohm
R = V/i [W] = [VA-1]
• Data una differenza di potenziale la corrente che scorre in un
conduttore dipende dalla sua resistenza V = Ri
• Un materiale
obbedisce alla legge di
Ohm se il valore della
resistenza non
dipende dalla polarità
della d.d.p. applicata
• Può succedere che un materiale abbia un andamento corrente
tensione come quello del grafico rappresentato di destra; allora
diremo che il materiale è un semiconduttore
• L’andamento della resistività di un conduttore con la temperatura è
lineare (cresce se cresce la temperatura). In prossimità dello zero
assoluto la resistività dei metalli non diventa zero
Resistenza e conducibilità
di un materiale
Conoscendo il valore della conducibilità
o resistività di un materiale si può
risalire alla resistenza che offre un tratto
di filo di quel materiale.
E V L
J i A
L
R
A
La resistività è data da: = E/J [Wm]
In questa espressione non si tiene conto
della forma del materiale.
Si può parlare di conducibilità elettrica
ricordando che
s 1/
J=sE
Gas di elettroni liberi
Il moto degli elettroni è un moto caotico con una
velocità efficace pari a:
veff = 1.6 106 m/s
Applicare una d.d.p. ai capi di un filo significa fare
in modo che l’agitazione termica risenta un po’
(circa 10-6) dell’effetto del campo elettrico
applicato. Un elettrone di massa m subirà una
accelerazione a pari a = F/m = eE/m
Se pensiamo gli elettroni come un gas perfetto, nel tempo tra due
collisioni l’accelerazione subita sarà a vd/ e quindi
vd = eE/m combinata con J = nevd si ottiene
E = (m/e2n)J
Dove = m/e2n è la resistività di un metallo.
La potenza elettrica
La batteria stabilisce una tensione costante V ai capi
del dispositivo con Va > Vb e la corrente che vi scorre è
costante e vale i è dq = i dt
L’energia potenziale ai capi del dispositivo diminuisce di
dU = dq V = idt V
a
+
_
questa energia si trasformerà, per esempio in calore, e
la potenza associata a questa trasformazione è
P=iV
[1VA] = 1W
Se il dispositivo è una resistenza avremo anche le relazioni
P = i2 R
i
o
P = V2/R
b
La superconduttività
(Kammerling Onnes 1911)
I circuiti elettrici
i
Per far circolare una carica in un filo conduttore
bisogna disporre di un generatore. Nelle batterie le +
reazioni chimiche forniscono l’energia necessaria a _
creare una ddp ai suoi morsetti. Se la batteria è
collegata ad un circuito resistivo le cariche si
spostano attraverso il circuito (elettroni e ioni) e
quindi nel circuito circola una corrente i. Se il circuito
è molto resistivo la batteria deve fare molto lavoro
per spostare le cariche, quindi la batteria si scarica
più facilmente
dL = E dq
a
b
dove E è la forza elettromotrice
I circuiti elettrici a valle della sorgente elettrica risentono di questo
campo e se hanno cariche libere a disposizione le vedono muoversi.
Corrente elettrica: conservazione
dell’energia
La f.e.m. E è il lavoro che una sorgente compie per portare una
carica da un potenziale basso ad uno più alto [volt]
La potenza dissipata da una resistenza nell’intervallo di tempo dt è
P = i2R che equivale ad un Lavoro dL = i2R dt.
La batteria dovrà fare un lavoro dL = E dq = E idt ovvero
E i dt = i2Rdt
E = iR (è la f.e.m. che deve fare la batteria per far passare la
corrente i nel circuito resistivo)
i = E /R
Corrente elettrica:
metodo del potenziale
A
Per comprendere questo metodo dobbiamo
definire le legge dei nodi e delle maglie di
“Kirchhoff”
Legge delle maglie ∑ (iR + E) = 0 nel circuito di figura partendo
da a sarà E – iR + = 0 E = iR
Legge dei nodi ∑ i = 0 nei circuiti con più maglie quando si
incontrano più rami si parla di nodo e nei nodi la corrente deve
essere zero. Normalmente le sorgenti di f.e.m. hanno una loro
resistenza interna, quindi
E ir iR 0
E
i
Rr
Resistenze in serie
• La resistenza equivalente di due o più
resistenze in serie è la somma delle
resistenze Req = ∑i Ri
• Se si vuole conoscere la ddp fra due punti
A e B si percorre il circuito da A fino a B
facendo la somma algebrica delle cadute di
tensione
• Siccome nelle sorgenti reali si ha una
resistenza interna r. La potenza erogata da
una batteria dovrà tenere conto della perdita
interna.
La ddp sia V = E – ir P = i(E – ir) = iE - i2r
potenza disponibile
i2r è la potenza dissipata internamente al generatore
iE è la potenza erogata dal generatore
Resistenze in parallelo
Nelle resistenze in parallelo si conosce la ddp ai capi
di ciascuna, ma non la corrente che vi circola
attraverso, quindi ciascun ramo avrà una corrente ij =
V/Rj .
La corrente che deve essere erogata dalla batteria
sarà
i = V (1/R1 +1/R2 …+ 1/Rn)
1
n 1
1
Req
Ri