Statistica Applicata all`edilizia Lezione 2: Analisi descrittiva dei dati

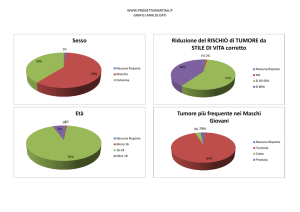
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Statistica Applicata all’edilizia
Lezione 2: Analisi descrittiva dei dati
Orietta Nicolis
E-mail: [email protected]
1 marzo 2011
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Programma
1
Analisi grafica dei dati
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
2
Indici di posizione e variabilità
Indici di posizione
Indici di dispersione
Il boxplot
3
Analisi di correlazione tra due o più variabili
4
Casi di studio
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Programma
1
Analisi grafica dei dati
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
2
Indici di posizione e variabilità
Indici di posizione
Indici di dispersione
Il boxplot
3
Analisi di correlazione tra due o più variabili
4
Casi di studio
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Tipi di variabili
1
variabili
quantitative
discrete continue
Orietta Nicolis
qualitative
norminali ordinali
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Numero abitazioni: nuovi fabbricati e
ampliamenti
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Grafico per i valori assoluti e per percentuali
180
160
Nuovi fabbricati
Ampliamenti
Totale
N. abitazioni
156.388
17.002
173.39
156.388
140
120
100
80
60
40
17.002
20
0
Nuovi fabbricati
Nuovi fabbricati
Ampliamenti
Totale
N. abitazioni
156.388
17.002
173.39
%
90.19
9.81
100
Orietta Nicolis
Ampliamenti
9.81%
Nuovi fabbricati
Ampliamenti
90.19%
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Fabbricati residenziali per numero di
abitazioni e ripartizione geografica. Anno 2000
(composizione percentuale)
Nord
Centro
Sud
Isole
Italia
1
37.2
37.6
56.5
64.6
44.0
2
18.7
18.9
15.7
16.2
17.9
3-15
37.7
36.9
23.7
16.8
32.6
Orietta Nicolis
16-30
4.8
5.0
3.1
1.9
4.2
oltre 30
1.6
1.5
1.0
0.5
1.3
Statistica Applicata all’edilizia
Totale
100.0
100.0
100.0
100.0
100.0
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Grafico del numero di abitazioni
70
60
50
Nord
Centro
Sud
Isole
Italia
40
30
20
10
0
1 abitaz.
2 abitaz.
3-15 abitaz.
Orietta Nicolis
16-30
abitaz
oltre 30
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: % di fabbricati residenziali per tipo di
struttura portante e numero di piani. Anno 2000
1 piano
2 piani
3 piani
4 piani
5 piani
6 piani
7 piani
8 piani
9 piani
Totale
Pietra e mattoni
2.8
11.9
7.8
2.2
0.2
–
–
–
–
24.9
Cemento armato
6.6
24.6
25.8
7.8
2.7
1.0
0.4
0.2
0.2
69.3
Orietta Nicolis
Statistica Applicata all’edilizia
Altro
0.7
2.2
2.0
0.6
0.1
0.1
0.1
0.2
0.2
5.8
Totale
10.2
38.7
35.6
10.6
3.0
1.1
0.4
0.2
0.2
100
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Grafici fabbricati
0%
%fabbricati
totali per n. di piani
% fabbricati per materiale e n. piani
30
0%
Mattone e pietra
Cemento armato
Altro
0%
1%
25
11%
20
3%
10%
15
10
5
36%
0
1 2 piani 3 piani 4 piani 5 piani 6 piani 7 piani 8 piani 9 piani
piano
Orietta Nicolis
Statistica Applicata all’edilizia
39%
1 piano
2 piani
3 piani
4 piani
5 piani
6 piani
7 piani
8 piani
9 piani
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: abitazioni in fabbricati per numero di stanze
e tipologia di comune. Anno 2000.
N. stanze:
Capoluoghi
Altri Comuni
Italia
1 s.
3.2
2.4
2.6
2 s.
18.6
15.8
16.3
3 s.
25.6
24.5
24.6
4 s.
31.3
29
29.5
5 s.
17.3
20.6
20
35
30
25
Capoluoghi
Altri
Italia
20
15
10
5
0
1 stanza 2 stanze 3 stanze 4 stanze 5 stanze
Orietta Nicolis
oltre 5
Statistica Applicata all’edilizia
oltre 5
4
7.6
7
Totale
100
100
100
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Andamenti (o trends) nel tempo
Esempio: Andamento dell’Indice (trimestrale) della Produzione delle
Costruzioni (IPC) dal gennaio 1995 a marzo 2006.
IPC
79.7
90.5
82.5
93.5
79.1
92.8
...
IPC
140
130
120
110
100
90
80
70
60
19
95
1 9 /1
95
1 9 /4
96
1 9 /3
97
1 9 /2
98
1 9 /1
98
1 9 /4
99
2 0 /3
00
2 0 /2
01
2 0 /1
01
2 0 /4
02
2 0 /3
03
2 0 /2
04
2 0 /1
04
2 0 /4
05
2 0 /3
06
/2
Tempo (t)
1995/1
1995/2
1995/3
1995/4
1996/1
1996/2
...
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Andamento dei prezzi medi mensili delle case nel Regno
Unito (UK) da agosto 2004 al gennaio 2007.
£180,000
£175,000
£170,000
£165,000
£160,000
£155,000
£150,000
£145,000
£140,000
g04
O
ct
-0
4
D
ec
-0
4
Fe
b05
Ap
r-0
5
Ju
n05
Au
g05
O
ct
-0
5
D
ec
-0
5
Fe
b06
Ap
r-0
6
Ju
n06
Au
g06
O
ct
-0
6
D
ec
-0
6
Prezzi
£153.743
£153.727
£152.159
£153.439
£152.623
£151.757
£152.879
£153.876
£156.128
...
Au
Tempo (t)
Aug-04
Sep-04
Oct-04
Nov-04
Dec-04
Jan-05
Feb-05
Mar-05
Apr-05
...
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Andamento Euribor (a 3 mesi) dal 1 gennaio 1999 al 19
ottobre 2001.
6.000
5.000
4.000
3.000
2.000
1.000
Orietta Nicolis
Statistica Applicata all’edilizia
10-Oct-01
26-Jun-01
17-Aug-01
03-May-01
17-Jan-01
12-Mar-01
02-Oct-00
23-Nov-00
09-Aug-00
25-Apr-00
16-Jun-00
10-Jan-00
02-Mar-00
17-Nov-99
24-Sep-99
03-Aug-99
19-Apr-99
10-Jun-99
0.000
01-Jan-99
Euribor
3.245
3.234
3.222
3.214
3.206
3.196
3.193
3.190
...
24-Feb-99
Tempo (t)
01 − Jan − 99
04 − Jan − 99
05 − Jan − 99
06 − Jan − 99
07 − Jan − 99
08 − Jan − 99
11 − Jan − 99
12 − Jan − 99
...
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Grafici per il monitoraggio strutturale
Esempio: Spostamenti a Finale Ligure dal 21 giugno 2002 al 6
novembre 2002.
Liv 1
Liv 2
Liv 3
45.5
31
45
38
29
44.5
mm
mm
mm
30
44
37.5
43.5
28
Jul02
Aug02
Oct02
37
Jul02
Liv 4
Aug02
Oct02
Jul02
Liv 5
35
Oct02
Liv 6
18
42
17
34
mm
mm
34.5
mm
Aug02
41
40
33.5
16
15
14
Jul02
Aug02
Oct02
Jul02
Liv 7
Aug02
Oct02
Jul02
Liv 8
Aug02
Oct02
Liv 9
49
21.4
36
21
20.8
48.5
mm
mm
mm
21.2
35.5
48
35
20.6
Jul02
Aug02
Oct02
Orietta Nicolis
Jul02
Aug02
Oct02
Jul02
Statistica Applicata all’edilizia
Aug02
Oct02
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Spostamenti (Ara Pacis)
Ch 4
2
1
mm
0
−1
−2
−3
−4
Oct03
Oct03
Nov03
Orietta Nicolis
Dec03
Dec03
Statistica Applicata all’edilizia
Jan04
Feb04
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Percentuali di abitazioni in fabbricati per
classe di superficie utile abitabile e tipologia di
comune per l’anno 2000.
m2 :
Capol.
Altri
Italia
0 − 45
13.2
10.5
11.0
46 − 75
38.4
37.3
37.6
76 − 95
30.6
25.9
26.8
Orietta Nicolis
96 − 110
8.6
11.9
11.2
Statistica Applicata all’edilizia
111 − 130
5.4
7
6.7
> 130
3.8
7.4
6.7
To
10
10
10
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Rappresentazioni tramite istogrammi.
Quando abbiamo un fenomeno quantitativo continuo con dati
raggruppati in classi si costruisce un istogramma procedendo come
segue:
1
Si dispongono i valori degli estremi degli intervalli delle classi
sull’asse delle ascisse ripettando l’unità di misura dell’asse
2
si tracciano dei rettangoli avendo come base gli estremi
dell’intervallo e come altezza la densità di frequenza li .
Attenzione : utilizzare le frequenze assolute o relative può
portare a grafici completamente sballati.
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio
Sia
ai : ampiezza di ciascuna classe
ni : numerosità (frequenza assoluta) di ciascuna classe
fi : frequenza relativa di ciascuna classe
li = ni /ai : densità di frequenza
considerando i dati per l’Italia e il numero di fabbricati nuove
abitazioni (pari a 156388) si ha:
Classi
0a 45
45a 75
75a 95
95a 110
110a 130
130a300
Tot.
fi
0.11
0.376
0. 268
0.112
0.067
0.067
100
ni
156388
58801.888
41911.984
17515.456
10477.996
10477.996
156388
Orietta Nicolis
ai
45
30
20
15
20
170
li
382.28
1960.06
2095.60
1167.70
523.90
61.64
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Istogramma
2500
2000
1500
1000
500
50
100
Orietta Nicolis
150
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Variazioni del tasso Euribor.
450
400
350
300
250
200
150
100
50
0
−0.04 −0.03 −0.02 −0.01
Orietta Nicolis
0
0.01
0.02
0.03
0.04
Statistica Applicata all’edilizia
0.05
0.06
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Grafici per il monitoraggio strutturale
Esempio: Istogramma degli spostamenti a Finale Ligure dal 21
giugno 2002 al 6 novembre 2002.
Liv 1
Liv 2
Liv 3
1000
800
600
600
600
400
400
400
0
200
200
200
28
29
30
31
0
43.5
44
mm
Liv 4
800
2500
600
2000
44.5
mm
Liv 5
45
45.5
0
37
37.5
mm
Liv 6
38
800
600
1500
400
400
1000
200
0
200
500
33.5
34
34.5
35
0
40
mm
Liv 7
500
41
mm
Liv 8
0
42
14
15
16
17
mm
Liv 9
18
600
600
400
300
200
400
400
200
200
100
0
20.6
20.8
21
21.2
mm
21.4
0
Orietta Nicolis
48
48.5
mm
49
0
Statistica Applicata all’edilizia
35
35.5
mm
36
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Grafico di dispersione
Esempio: Relazione tra il prezzo di vendita delle case di una
determinata città e il valore accertato.
Valore accertato
accertato
78.17
80.24
74.03
86.31
75.22
...
Prezzo di
vendita
94.1
101.9
88.65
115.5
87.5
...
120
110
100
Orietta Nicolis
90
80
70
60
50
40
50
55
60
65
Statistica Applicata all’edilizia
70
75
80
85
90
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
Esempio: Spostamenti (Ara Pacis)
Ch 4, R2=0.963
3
2
1
0
−1
−2
−3
−4
9
10
11
12
Orietta Nicolis
13
14
15
16
17
Statistica Applicata all’edilizia
18
19
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Indici di posizione
Indici di dispersione
Il boxplot
Programma
1
Analisi grafica dei dati
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
2
Indici di posizione e variabilità
Indici di posizione
Indici di dispersione
Il boxplot
3
Analisi di correlazione tra due o più variabili
4
Casi di studio
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Indici di posizione
Indici di dispersione
Il boxplot
Indici di posizione
Minimo e Massimo: x(1) e x(n) ;
Media aritmetica (semplice e ponderata):
Pn
P1
i=1 xi pi
pi
1
n
Pn
i=1
Mediana:
Quantili (quartili e percentili);
Orietta Nicolis
Statistica Applicata all’edilizia
xi e
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Indici di posizione
Indici di dispersione
Il boxplot
La mediana
La mediana è quel valore che, una volta ordinati i dati del campione,
lascia alla sua sinistra e alla sua destra la metà del campione
La mediana divide a metà la distribuzione dei dati
Può essere calcolata solo per fenomeni ordinabili
Se n è l’ampiezza del campione, si procede così:
1) si ordinano i dati in ordine crescente
2) si calcola il valore (n + 1)/2
3a) se esiste (n + 1)/2 (caso n dispari) la mediana è quel valore.
3b) se (n + 1)/2 non è un numero intero (caso n pari)
fenomeno quantitativo: si fa la media tra il valore precedente e
quello successivo alla posizione (n + 1)/2
fenomeno qualitativo: si confrontano le modalità di posto
precedente e successivo alla posizione (n + 1)/2 e se coincidono
quella è la mediana, altrimenti la mediana è indeterminata.
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Indici di posizione
Indici di dispersione
Il boxplot
Indici di dispersione
Scarto interquartile: Q3 − Q1 ;
Campo di variazione: x(n) − x(1) ;
Pn
La varianza: n1 i=1 (xi − x)2 ;
√
Scarto quadratico medio: σ 2 ;
√
Coefficiente di variazione:
σ2
µ ,
Orietta Nicolis
con µ =
1
n
Pn
i=1
Statistica Applicata all’edilizia
xi ;
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Indici di posizione
Indici di dispersione
Il boxplot
Il boxplot
La distribuzione di una variabile statistica viene rappresentata
come una scatola. gli estremi della scatola sono Q1 e Q3 ;
la scatola è tagliata dalla mediana;
i baffi della scatola:
- baffo superiore: Q1 − 1.5 · (Q3 − Q1 );
- baffo inferiore: Q3 + 1.5 · (Q3 − Q1 );
se non ci sono valori in corrispondenza dei baffi questi si
accorciano al dato più vicino tutti i valori fuori dai baffi si segnano
come punti isolati
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Indici di posizione
Indici di dispersione
Il boxplot
Esempio: Valori di PM10 .
Inverno
Estate
160
62
187
59
Orietta Nicolis
141
49
88
61
110
71
Statistica Applicata all’edilizia
66
59
74
45
156
34
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Programma
1
Analisi grafica dei dati
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
2
Indici di posizione e variabilità
Indici di posizione
Indici di dispersione
Il boxplot
3
Analisi di correlazione tra due o più variabili
4
Casi di studio
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
La covarianza tra X ed Y
La covarianza è un indice che misura la dispersione delle coppie
di punti dal baricentro.
La covarianza, al contrario della varianza, si occupa anche di
misurare l’eventuale direzione della variabilità
La formula della covarianza è
n
σxy = Cov(X , Y ) =
1X
(xi − x̄n )(yi − ȳn )
n
i=1
ovvero (formula alternativa)
n
σxy =
1X
(xi · yi ) − (x̄n · ȳn )
n
i=1
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
L’indice di correlazione tra X ed Y
Vale la seguente relazione
−σx · σy ≤ σxy ≤ σx · σy
e quindi possiamo definire l’indice di correlazione
ρxy =
σxy
σx · σy
− 1 ≤ ρxy ≤ 1
ρxy =0 solo se X ed Y sono incorrelate
ρxy =1 solo se X ed Y sono in relazione lineare diretta
ρxy =-1 solo se X ed Y sono in relazione lineare inversa
N.B.: L’assenza di relazione lineare non implica che non siano
presenti altri tipi di relazione
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Esercizi
Determinare l’indice di correlazione lineare per le seguenti misure:
1
Spostamenti di Finale rispetto alla temperatura.
2
Spostamenti di Ara Pacis rispetto temperatura.
3
Spostamenti del misuratore di giunti Mg1 del Ponte di Certosa
rispetto alla temperatura.
4
Indice dei prezzi delle case e indice Euribor.
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Programma
1
Analisi grafica dei dati
Grafici per dati qualitativi: a barre e a torta
Grafici per serie storiche: andamenti
Grafici per dati quantitativi: Istogrammi
Grafico di dispersione
2
Indici di posizione e variabilità
Indici di posizione
Indici di dispersione
Il boxplot
3
Analisi di correlazione tra due o più variabili
4
Casi di studio
Orietta Nicolis
Statistica Applicata all’edilizia
Analisi grafica dei dati
Indici di posizione e variabilità
Analisi di correlazione tra due o più variabili
Casi di studio
Esercizi
Eseguire un’analisi statistica descrittiva dei seguenti insiemi di dati e
commentare i risultati ottenuti:
1
Indice della produzione nelle costruzioni (IPC)
2
Indice Euribor
3
Prezzi delle case in UK
4
Monitoraggio degli spostamenti di Finale Ligure.
5
Monitoraggio degli spostamenti di Ara Pacis.
6
Monitoraggio dei misuratori di giunti del ponte di Certosa.
Orietta Nicolis
Statistica Applicata all’edilizia