G. Legnani, G. Palmieri - Fondamenti di Meccanica e Biomeccanica del Movimento - Errata Corrige - 26 maggio 2017
G. Legnani, G. Palmieri
Fondamenti di
Meccanica e Biomeccanica del Movimento
Città Studi - ISBN 978-88-251-7407-6
http://robotics.unibs.it
http://www.meccanicadellemacchine.it
http://www.cittastudi.it/catalogo/ingegneria/fondamenti-di-meccanica-e-biomeccanica-del-movimento-3562
inviare commenti e suggerimenti a
[email protected] e [email protected]
Errata Corrige e Ampliamenti
26 maggio 2017
Riferimento
Errata
Corrige
xvi
riga 28
Gabriele Baronio
Stefano Uberti
27
Fig. 2.6
fascio muscolare
fibra muscolare
29
Fig. 2.9
F=4 V=4 ∆L= 1
F=4 V=1 ∆L=1
34
r.17 dal fondo
peso specifico
densità
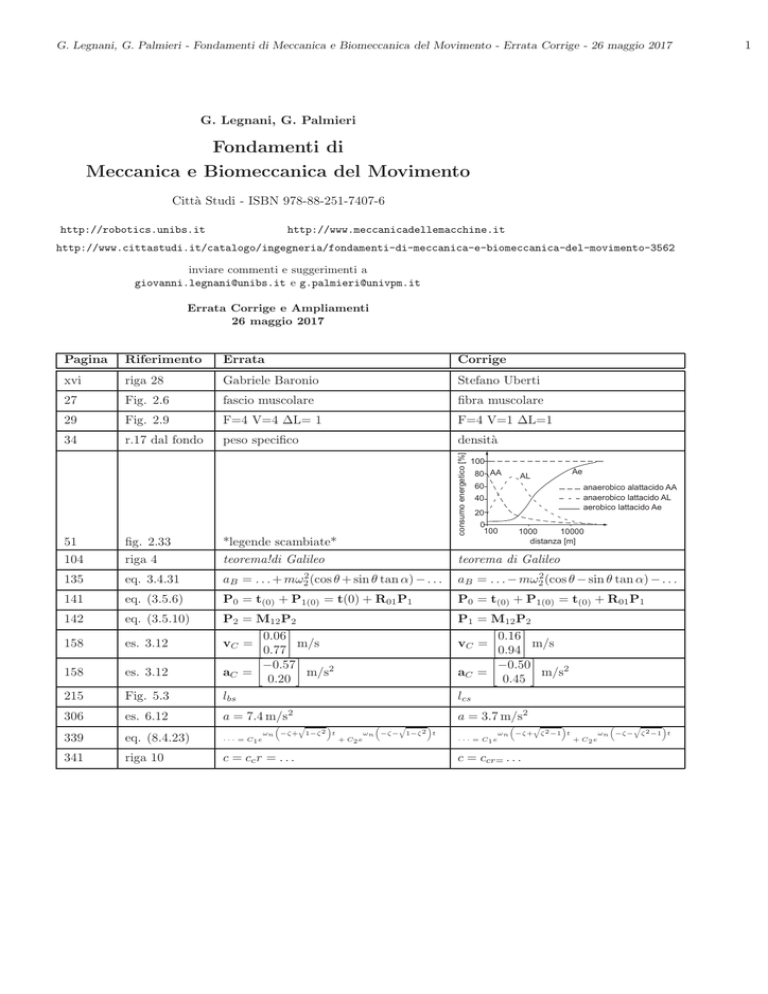
consumo energetico [%]
Pagina
51
104
fig. 2.33
riga 4
*legende scambiate*
teorema!di Galileo
. . . + mω22 (cos θ + sin θ tan α) − . . .
100
80 AA
AL
60
anaerobico alattacido AA
anaerobico lattacido AL
aerobico lattacido Ae
40
20
0
100
Ae
1000
10000
distanza [m]
teorema di Galileo
aB = . . . − mω22 (cos θ − sin θ tan α) − . . .
135
eq. 3.4.31
aB =
141
eq. (3.5.6)
P0 = t(0) + P1(0) = t(0) + R01 P1
142
eq. (3.5.10)
158
es. 3.12
158
es. 3.12
215
Fig. 5.3
P2 = M12 P2
0.06
vC =
m/s
0.77 −0.57
aC =
m/s2
0.20
lbs
P1 = M12 P2
0.16
vC =
m/s
0.94 −0.50
aC =
m/s2
0.45
lcs
306
es. 6.12
a = 7.4 m/s2
a = 3.7 m/s2
339
eq. (8.4.23)
q
q
ωn −ζ+ 1−ζ 2 t
ωn −ζ− 1−ζ 2 t
· · · = C1 e
+ C2 e
q
q
ωn −ζ+ ζ 2 −1 t
ωn −ζ− ζ 2 −1 t
· · · = C1 e
+ C2 e
341
riga 10
c = cc r = . . .
c = ccr= . . .
P0 = t(0) + P1(0) = t(0) + R01 P1
1
2
G. Legnani, G. Palmieri - Fondamenti di Meccanica e Biomeccanica del Movimento - Errata Corrige - 26 maggio 2017
Pagina
Riferimento
Errata
(
A = C sin θ
B = C cos θ
Corrige
(
A = C sin α
B = C cos α
346
eq. (8.5.11)
347
riga 2
fa = 0.4
fa = 0.6
348
riga 5
349
riga 10
· · · = 11.05 N
· · · = 265.62 N
√
ω/ωn > 2
372
eq. (9.3.2)
Sx = . . .
Sy = . . .
376
righe 14, 16
P
N
386
eq. (9.7.5)
··· = −
386
riga 7
E
Sy = 0 → Sy = 0
ρ
in cui Sy rappresenta . . . all’asse y . . .
E
Sz = 0 → Sz = 0
ρ
in cui Sz rappresenta . . . all’asse z . . .
433
Es. 11.1 riga 3
del braccio
dell’avambraccio
436
riga 4
438
riga 13
§4.12
§4.2
439
439
eq. (11.6.2)
eq. (11.6.2)
439
eq. (11.6.2)
487
eq. (12.9.1)
539
Fig. 13.43
asse y fig. dx
545
eq. (13.3.6)
546
eq. (13.3.10)
547
547
547
547
548
eq.
eq.
eq.
eq.
eq.
(13.3.11)
(13.3.11)
(13.3.11)
(13.3.11)
(13.3.12)
ω/ωn > 2
§4.12
Ixy =
Iyz =
R
R
R
Sy = . . .
... ≃
... ≃
Ixz = . . . ≃
i
i
−
d1 d2
F1 + F2
P
P
P
b1 ϑ̇2 Cϑ
−b1 ϑ̇2 Sϑ
··· = −
§4.2
...
Ixy = −
...
b2 ε̇2
1 Cε1
−b2 ε̇2
1 S ε1
R
R
... ≃ −
P
...
P
Iyz = − . . . ≃ − . . .
R
P
Ixz = − . . . ≃ − . . .
i
i
− 2
2
d1 d2
F2 + F3
...
. . . −a3 = 0
. . . −a4 = 0
Sx = . . .
b3 ε̇2
2 Cε2
−b3 ε2
2 S ε2
= aGcs − . . .
(Ggm − Gcs )
= aGcm − . . .
(Gpd − Ggm )
Mcv = · · · − f mpd Gpd y Cǫ2
−a2 ε̇2
3 Cε3
a2 ε̇2
3 S ε3
. . . −a4 = 0
. . . −a3 = 0
b1 Cϑ
b2 Cε1
b3 Cε2
−a2 Cε3
−b1 Sϑ
−b2 Sε1
−b3 Sε2
a2 Sε3
= aA − . . .
(Ggm − A)
(2 volte)
= aB − . . .
(Gpd − B)
(2 volte)
Mcv = · · · − f mpd aGpd y Cǫ2
ϑ̇2
ε̇2
1
ε̇2
2
ε̇2
3












