( ) ∫ ∫

Dielettrici
I.
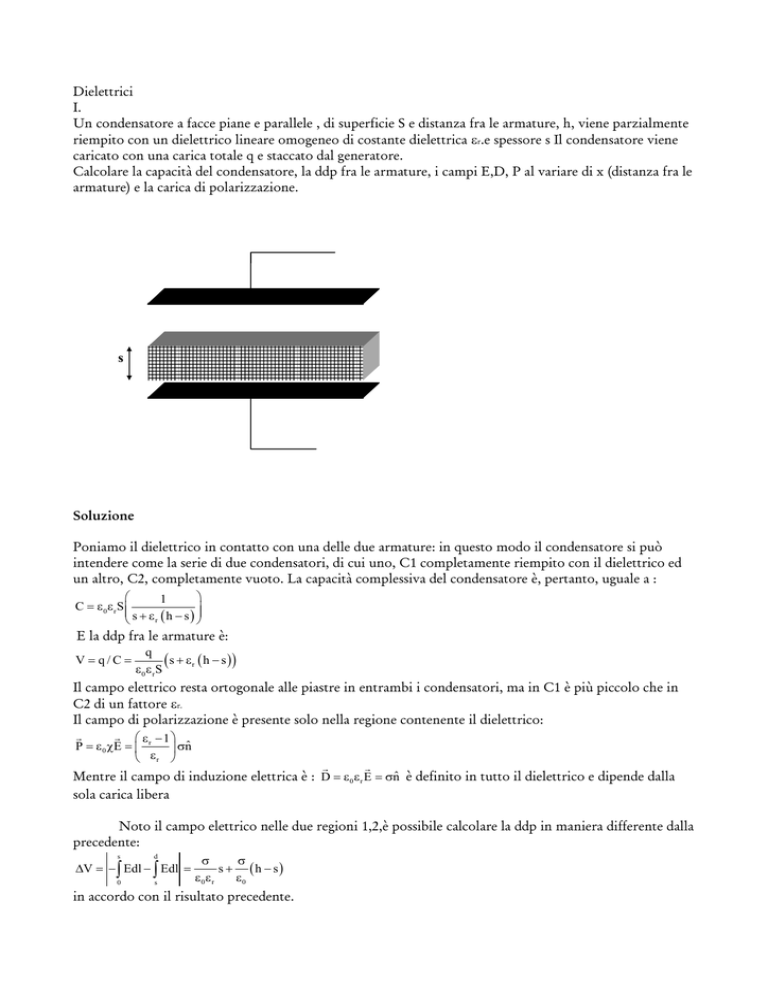
Un condensatore a facce piane e parallele , di superficie S e distanza fra le armature, h, viene parzialmente
riempito con un dielettrico lineare omogeneo di costante dielettrica εr.e spessore s Il condensatore viene
caricato con una carica totale q e staccato dal generatore.
Calcolare la capacità del condensatore, la ddp fra le armature, i campi E,D, P al variare di x (distanza fra le
armature) e la carica di polarizzazione.
s
Soluzione
Poniamo il dielettrico in contatto con una delle due armature: in questo modo il condensatore si può
intendere come la serie di due condensatori, di cui uno, C1 completamente riempito con il dielettrico ed
un altro, C2, completamente vuoto. La capacità complessiva del condensatore è, pertanto, uguale a :
⎛
⎞
1
C = ε 0 ε r S ⎜⎜
⎟⎟
⎝ s + εr ( h − s ) ⎠
E la ddp fra le armature è:
V = q/C =
q
( s + εr ( h − s ) )
ε0 ε r S
Il campo elettrico resta ortogonale alle piastre in entrambi i condensatori, ma in C1 è più piccolo che in
C2 di un fattore εr.
Il campo di polarizzazione è presente solo nella regione contenente il dielettrico:
r
r ⎛ ε −1 ⎞
P = ε 0 χE = ⎜ r
⎟ σnˆ
⎝ εr ⎠
r
r
Mentre il campo di induzione elettrica è : D = ε0 ε r E = σnˆ è definito in tutto il dielettrico e dipende dalla
sola carica libera
Noto il campo elettrico nelle due regioni 1,2,è possibile calcolare la ddp in maniera differente dalla
precedente:
s
d
0
s
∆V = − ∫ Edl − ∫ Edl =
σ
σ
s + (h − s)
ε0 ε r
ε0
in accordo con il risultato precedente.
2. Un condensatore sferico con le armature distanti d e raggi delle stesse uguali ad R1, R2, viene riempito
parzialmente con un dielettrico di costante dielettrica εr. e spessore d/3. Le armature del condensatore,
prima dell’inserimento del dielettrico erano state portate ad una ddp di ∆V0, indi la batteria era stata
staccata. Determinare le densità e le cariche di polarizzazione nella configurazione finale ed la ddp fra le
armature
Soluzione.
Il campo e.s in assenza di dielettrico è :
r
E0 =
q
r̂
4πε 0 r 2
nella regione compresa fra le armature ed è nullo all’esterno di queste.
Pertanto la ddp fra le armature è
R2
∆V0 = − ∫ Edl =
R1
q
4πε 0
1 ⎞ q
⎛ 1
−
⎜
⎟=
R1
R2
⎝
⎠ C0
ed infine:
1
1 ⎛ R2 − R1 ⎞
=
⎜
⎟
C0 4πε 0 ⎝ R1R2 ⎠
La presenza del dielettrico, cambia il valore della capacità che può essere letta come la serie di due
capacità, di cui una, C1 , con dielettrico:
1
1
=
C1 4πε 0 ε e
⎛ R3 − R1 ⎞
⎜
⎟
⎝ R1R3 ⎠
E l’altra, C2, senza dielettrico
1
1 ⎛ R2 − R3 ⎞
=
⎜
⎟
C2 4πε 0 ⎝ R2R3 ⎠
Dove R3 =R1+d/3.
In fine la ddp nella configurazione con dielettrico è la seguente:
q
q
=
C 12πε 0 ε e
⎛ R2 + 2R1ε e ⎞
d⎜
⎟
⎝ R1R3R2 ⎠
Il vettore di polarizzazione, nella regione in cui è presente il dielettrico è
r
r
⎛ ε −1 ⎞ q
P(r) = ε 0 χE(r) = ⎜ r
rˆ
⎟
2
⎝ ε r ⎠ 4πr
Pertanto, sulla superficie del dielettrico che si affaccia sull’armatura interna, la densità di carica di
polarizzazione è:
⎛ ε −1 ⎞ q
σp + = ⎜ r
⎟
2
⎝ ε r ⎠ 4πR1
⎛ ε −1 ⎞ q
σp − = ⎜ r
⎟
2
⎝ ε r ⎠ 4πR3
Assumendo la carica libera positiva collocata sull’armatura più grande.
Infine, le cariche di polarizzazione sono:
⎛ ε −1 ⎞
qp+ = ⎜ r
⎟ q = qp−
⎝ εr ⎠
III.
In un condensatore a facce piane e parallele è stata inserita una sostanza dielettrica con costante dielettrica relativa
εr=1+x/d. Le armature del condensatore hanno i lati di lunghezza l ed a ed hanno una distanza d (direzione x).
Calcolare la capacità del condensatore e la carica di polarizzazione.
Soluzione
a) La capacità C può essere calcolata considerando l’intero condensatore come una serie di condensatori
infinitesimi. Pertanto C si ottiene integrando le capacità elementari:
-
x
d
a
l
+
d
1
1 d d
d
dx =
∫ d + x dx = ε la ln(2)
la
la
ε
ε
ε
(x)
0 0
0
0 0 r
C−1 = ∫
e
C = C 0 / ln(2)
b)La densità di carica superficiale si stima a partire dal vettore di densità di polarizzazione:
ε −1
x
P(x) = ε0 χE = r
σ=
σ
εr
d+x
σ
indica il campo elettrico nel condensatore
εr (x)ε0
Infine la densità di superficie della carica di polarizzazione è:
dove E(x) =
r
σ P (x) = nˆ ⋅ P(x) =
x
σ
d+x
e varia da zero a σ/2, passando dall’armatura positiva a quella negativa. Pertanto, la carica di polarizzazione
superficiale totale e` diversa da zero:
q pol,1 = q / 2
La carica di polarizzazione sulla superficie non è globalmente nulla, pertanto deve esistere una densità di volume
di carica di polarizzazione:
∂
d
ρP (x) = − P(x) = −
σ
∂
(d + x) 2
Ed, infine, la carica di polarizzazione associata è:
d
d
0
(d + x) 2
q pol,2 = ∫ dv ρP (x) = − al ∫ dx
σ = −q / 2
IV
Un condensatore sferico,con le armature distanti d = 2,5 mm, e superficie esterna S=12 cm2 viene collegato con
una resistenza R0= 12 Ω ed un generatore di forza elettromotrice V0= 1kV e resistenza interna r = 2Ω. L’energia
perduta per effetto Joule, nel tempo necessario a raggiungere una condizione di equilibrio è di 2 10-5J.
Determinare, all’equilibrio, il valore della capacità del condensatore, della costante dielettrica del materiale che
riempie completamente il condensatore e della carica di polarizzazione.
Soluzione
Il circuito equivalente al sistema è costituito dal capacitore C , collegato in serie con la resistenza R = r+R0=14Ω
e dal generatore ideale V0.
La carica sul condensatore cresce nel tempo secondo la legge:
q(t) = q 0 (1− e − t / τ ) , q 0 = CV0 ,
τ=RC
La corrente segue la legge:
i(t) = i 0 e− t / τ , i0=V0/R.
L’energia perduta per effetto Joule, si ricava integrando sull’intervallo di tempo 0-∞ la potenza dissipata :
∞
2
V02 C
2
0
Notiamo che dopo un tempo pari a 3 il sistema può considerarsi all’equilibrio, infatti , nel precedente integrale,
sostituendo al valore ∞ il valore 3 si ha un modifica del risultato pari allo 0,997 del risultato effettivo .
W = ∫ R ( i0 e
−t / τ
)
dt =
Conoscendo il valore di W si ricava C:
2W
C = 2 =4,0 10-11 F
V0
D’altra parte, C= C0 εr,
dove C0 indica la capacità del condensatore vuoto. Per calcolare C0, osserviamo che il campo e.s. tra le armature
è:
r
q(t) rˆ
E(r, t)
, a≤r≤b,
4πε 0 ε r r 3
dove a, b indicano il raggio dell’armatura interna ed esterna, rispettivamente.
All’esterno del condensatore il campo e.s. è nullo.
Segue che la d.d.p. fra le armature è:
a
q ⎛1 1⎞
V(a) − V(b) = − ∫ E(r)dr =
⎜ − ⎟
4
πε
b⎠
0 ⎝a
b
e la capacità del condensatore è:
4πε 0
q
=
C0 ≡
ab
∆V b − a
Infine, sappiamo che:
S
= 9,8 mm
4π
ed, inoltre, a=b+d=7,27 mm
da cui risulta:
C0=3,17 pF ed εr=12,6.
b=
In ultimo, calcoliamo il valore della carica di polarizzazione.
La densità di carica di polarizzazione, σP è uguale al modulo del vettore di polarizzazione
r
r
r
q
P(r) = ε 0 ( ε r − 1) E(r) = ε 0 ( ε r − 1)
r
3
4πε 0 ε r r
In particolare
r
q
CV
σ P (a) = nˆ ⋅ P(a) = − ( ε r − 1)
= − ( ε r − 1)
4πε r a 2
4πε r a 2
nel caso in cui n̂ indichi la normale uscente dal mezzo verso
l’armatura interna
R0
S
d
r
V0
r
CV
σ P (b) = nˆ ⋅ P(b) = ( ε r − 1)
4πε r b 2
Nel caso in cui n̂ indichi la normale uscente dal mezzo verso l’armatura esterna.
Infine:
CV
q P − = σ P (a)4πa 2 = − ( ε r − 1)
εr
CV
εr
Quindi la carica totale di polarizzazione è nulla, come deve essere, mentre il modulo di ogni singolo valore è
qp=3,68 10-8C
q P + = σ P (b)4πb 2 = ( ε r − 1)