Elementi di Dinamica
ELEMENTI DI DINAMICA
Mentre la cinematica si limita allo studio delle possibilità di movimento di un certo
sistema ed alla relativa descrizione matematica, la dinamica si occupa delle cause che
determinano il moto stesso.
Il legame tra le grandezze dinamiche (forze, momenti, proprietà inerziali dei corpi etc.)
ed il moto che ne consegue è regolato dalle leggi di Newton.
Lo studio di un sistema dinamico è articolato in diverse fasi:
• Definizione di un modello fisico del sistema in esame
• Definizione del diagramma di corpo libero
• Definizione del modello matematico e soluzione
• Confronto con le evidenze sperimentali.
FORZE
Forza: azione di un corpo su un’altro corpo (unità di misura: Newton [N]) e tende a
spostare il corpo lungo la direzione in cui agisce.
La forza è una grandezza vettoriale, pertanto essa possiede
• modulo
• direzione
• verso
• punto di applicazione
Nel caso di forze applicate ai corpi rigidi ci si può
svincolare dal punto di applicazione e si può considerare
la forza come applicata in un punto qualsiasi della sua
retta d’azione (pricipio di trasmissibilità): considerare la
forza F come applicata in A o in B non cambia nulla dal
punto di vista delle reazioni sui vincoli in C e D
OPERAZIONI SULLE FORZE
Composizione di due forze:
Date due forze F1 ed F2 agenti sullo stesso
punto di un corpo rigido, esse possono
essere composte secondo la regola del
parallelogramma. La risultante R della
composizione ha sul corpo il medesimo
effetto del sistema di forze.
Scomposizione di due forze:
Analogamente una forza R può
essere sostituita dalla
scomposizione nelle sue
componenti F1 ed F2 lungo due
direzioni, facendo attenzione che
le rette d’azione passino per il
punto di applicazione di R
OPERAZIONI SULLE FORZE
Composizione di due forze parallele:
La forza F1 è applicata nel punto A1 e la forza F2 è
applicata al punto A2. F1 ed F2 sono parallele.
La risultante R delle due forze ha direzione
parallela alla direzione di F1 ed F2 .
La retta di applicazione di R passa per il punto A.
Il punto A si trova sommando e sottraendo una
forza ausiliaria F diretta lungo la congiungente i
punti A1 e A2.
Una forza F è applicata in A1 e la forza opposta –F
in A2.
Si determinano le risultanti R1 ed R2 nei punti A1
e A2 e si determina la risultante R= R1 + R2 con il
metodo già visto.
r
F1
A1
r r
F R1
r
F
r
R2
A
r
R2
r
A2 F2
r
R
r
R1
OPERAZIONI SULLE FORZE
Composizione di due forze parallele:
Per determinare analiticamente la posizione
geometrica della retta di azione r della risultante
R, si consideri che la retta r interseca il segmento
A1A2 nel punto AR. I triangoli A1ARA e il
triangolo F-F1-R1 costruito in A sono simili, così
come sono simili i triangoli A2ARA ed il triangolo
F-F2-R2. Pertanto si può scrivere:
A1A R A R A
=
F
F1
A2AR ARA
=
F
F2
A1A R
A2AR
=
A R A F2
F
⋅
= 2
F1 A R A F1
A1
r
F
r
r
F1
F2 r r
r
R
F R2 r
R1
r
r
R1
AR
A
r
r R2
F
r
F2
A2
F
F1
r
MOMENTO DI UNA FORZA
Misura la tendenza di una forza applicata ad un corpo a far ruotare il corpo stesso attorno a un
punto (nel piano) o ad un’asse (nello spazio). Se F è la forza applicata al punto A del corpo, il
momento di F rispetto al generico punto O è dato dal prodotto vettoriale:
r
j
r
r
r
r r
M O = r ∧ F = r ⋅ F ⋅ sin(α ) ⋅ k = b ⋅ F ⋅ k
r
i
Il momento della forza può essere espresso in funzione delle componenti della forza stessa.
Teorema di Varignon: il momento di una forza intorno ad un punto qualsiasi è pari alla somma
dei momenti delle componenti della forza intorno allo stesso punto.
r
r r
r
r
r r r
r r r r
M OR = r ∧ R = r ∧ (P + Q) = r ∧ P + r ∧ Q = M OP + M OQ
r
r r
momento di P rispetto ad O
M OP = r ∧ P
r
r r
momento di Q rispetto ad O
M OQ = r ∧ Q
COPPIA DI FORZE
Coppia di forze: insieme di due forze uguali in modulo e direzione, verso opposto e non allineate.
La risultante della coppia di forze è nulla.
Il momento della coppia di forze non dipende dal punto intorno al quale lo si calcola (vettore
libero):
r
r r
r
r r
r
r
r
M O = rB ∧ (−F) + rA ∧ F = −rB ∧ F + rA ∧ F =
r
r r r
r r
M O = (rA - rB ) ∧ F = r ∧ F
Il momento della coppia di forze (o semplicemente coppia), dipende solamente dal
modulo delle forze e dalla distanza d tra le rette di applicazione detto braccio della
coppia
r
r
r
M = [(a + d) ⋅ F − a ⋅ F] ⋅ k = d ⋅ F ⋅ k
TRASPOSIZIONE DI UNA FORZA
In generale, una forza
1) tende sempre a spostare il corpo a cui è applicata nella sua direzione e verso
2) tende a far ruotare il corpo a cui è applicata intorno ad un punto non appartenente
alla sua retta d’azione
Sistema iniziale: forza
applicata in A con momento
rispetto a B non nullo
Si aggiunge e sottrae
una forza in B, pari alla
forza iniziale in A
Il sistema finale: l’effetto è quello
di una “trasposizione” della
forza nel punto di interesse.
La forza F applicata in A può essere trasportata in B a patto di aggiungere al sistema
una coppia (momento di trasposizione) pari al momento che F applicata in A ha
rispetto a B.
RISULTANTE DI UN SISTEMA DI FORZE
Se su un corpo agiscono diverse forze, il sistema può essere semplificato mediante il
calcolo della risultante. Occorre determinare sia la somma R delle forze che il suo
punto di applicazione
Il calcolo della risultante di un
sistema di forze agenti su un
corpo si può eseguire mediante
la successiva applicazione della
regola del parallelogramma.
Può risultare un metodo
laborioso.
RISULTANTE DI UN SISTEMA DI FORZE
Se su un corpo agiscono diverse forze, il sistema può essere semplificato mediante il
calcolo della risultante. Occorre determinare sia la somma R delle forze che il suo
punto di applicazione
1 - Si sceglie un punto arbitrario O
2 - Si portano tutte le forze in O e si calcola la
somma R
3 - Si calcolano tutti i momenti delle forze rispetto
ad O
4 - Si sostituisce al sistema originario la somma R
delle forze in O più una coppia MO pari alla
somma dei momenti delle singole forze rispetto
ad O.
5 – Si sposta R in un punto generico B
aggiungendo il momento di trasporto.
6 – Si determina la distanza d del punto B da O
imponendo l’uguaglianza del momento di
trasporto M con MO
Tipi di forze
Le forze possono essere classificate secondo diversi criteri. Alcuni esempi:
• Forze concentrate: la zona su cui sono applicate si può ritenere puntiforme
rispetto alle dimensioni del corpo.
• Forze distribuite: la zona su cui sono applicate non può essere trascurata rispetto
alle dimensioni geometriche del corpo
• Forze esterne: sono applicate al corpo (o al sistema di corpi) dall’esterno
• Forze interne: sono forze scambiate tra gli elementi del sistema considerato
• Forze di contatto: dovute all’interazione diretta (contatto fisico) tra due corpi
• Forze di massa: sono correlate alle proprietà di massa del corpo (es: forza peso,
forze elettromagnetiche, forze di inerzia)
Nello studio di un sistema meccanico è importante identificare le forze in gioco
sulla base della natura dei fenomeni fisici coinvolti, della modalità con cui le forze
che ne derivano sono applicate.
È altresì importante impostare il problema coerentemente con i modelli meccanici
scelti per la rappresentazione del fenomeno in esame.
I TRE PRINCIPI DELLA DINAMICA
1) Una particella rimane a riposo o continua a muoversi di moto rettilineo uniforme
se la risultante di tutte le forze agenti su di essa è nulla (detto anche principio
d’inerzia)
2) L’accelerazione di una particella è proporzionale alla risultante delle forze agenti
su di essa ed è nella direzione e nel verso di tale risultante. La costante di
proporzionalità è pari alla massa della particella.
r
a=
r
∑ Fe
m
3) Le forze di azione e reazione tra corpi che interagiscono sono uguali in modulo
hanno la stessa retta d’azione e sono opposte in verso.
Le leggi della dinamica sono la base della meccanica classica e possono essere applicate direttamente ad un
enorme dominio di sistemi meccanici. I limiti di applicabilità si incontrano in quei problemi in che coinvolgono
i principi della meccanica quantistica o della fisica relativistica.
EQUAZIONI CARDINALI DELLA DINAMICA
Le azioni di inerzia sono definite come:
r
r
Fi = − m ⋅ a G
r
r
&
M iG = −I G ⋅ ω
forza d’inerzia applicata al baricentro
coppia d’inerzia baricentrica
L’introduzione delle azioni di inerzia è un artificio
che consente di scrivere delle equazioni di equilibrio
anche quando sono presenti degli stati di moto
accelerato
r r
∑ Fre +Fi r= 0
∑ M eG +M iG = 0
La seconda equazione può essere estesa ad un
caso più generale di equilibrio alla rotazione
intorno ad un qualsiasi punto P considerando il
momento rispetto a P di Fi.
r
r
r r
M i = M iG + h ∧ Fi
r r
∑ Fre +Fri = 0
∑ M e +M i = 0
EQUAZIONI CARDINALI DELLA DINAMICA
r r
∑ Fre +Fri = 0
∑ M e +M i = 0
Rappresentano l’equazione del moto del corpo o del
sistema di corpi (D’Alembert, 1743) ed esprimono
l’equilibrio dinamico di un sistema meccanico:
• in ogni istante, la somma di tutte le forze agenti sul
sistema più le forze d’inerzia è uguale a zero,
e
• la somma di tutti i momenti dovuti alle forze
esterne più il momento delle forze d’inerzia rispetto
ad un punto qualsiasi è uguale a zero.
Le equazioni vettoriali hanno validità
generale.
Nel caso di moto piano si traducono
nelle tre equazioni scalari:
∑F
∑F
∑M
ex
+Fix = 0
ey
+Fiy = 0
e
+M i = 0
STATICA
Problema di equilibrio statico: dato un corpo o un sistema di corpi tra loro
collegati mediante determinati vincoli, la soluzione di un problema di
equilibrio statico consiste nel determinare la relazione tra le forze agenti sul
corpo (o sistema di corpi) tale per cui il corpo resta fermo o in moto rettilineo
uniforme (accelerazione = 0).
In caso di moto accelerato, i metodi di risoluzione dei problemi di equilibrio
statico possono essere ancora impiegati a patto di introdurre nel computo le
azioni di inerzia.
La soluzione dei problemi di equilibrio statico presenta aspetti diversi a
seconda del grado di libertà del sistema in esame.
Es a: sistema ad 1 grado di libertà.
dato il valore della forza o momento agente in un
punto del sistema (es. la forza P) ed eventualmente di
più forze, calcolare il valore di un’altra forza o
momento in un altro punto del sistema (es. la coppia
C) in modo che il sistema sia fermo. Possono
eventualmente essere richieste le reazioni vincolari
(es. in O, A, B)
STATICA
Es b): sistema a più gradi di libertà.
Se il sistema ha più gradi di libertà, il problema di equilibrio è
analogo a quello per un grado di libertà, con la differenza che la
soluzione richiede il calcolo di tante forze (o coppie) quanti sono i
GdL del sistema.
Ad esempio, con rif. al cinematismo della figura b), noti i carichi
P1 e P2, può essere richiesto il calcolo di F2 e C1 che garantiscono
l’equilibrio. Possono essere richieste le reazioni in O ed A.
Es c): sistema a zero gradi di libertà (sistema isostatico).
Non esiste possibilità di movimento, il problema da risolvere,
noti i carichi agenti sul sistema, è il calcolo delle reazioni
vincolari.
Es d): sistema a gradi di libertà negativi (sistema iperstatico).
Se il calcolo dei GdL è inferiore a zero, non è possibile
determinare il valore delle reazioni vincolari dalle sole
equazioni di equilibrio (infinite soluzioni possibili), il modello
del corpo rigido è inadeguato ed è necessario introdurre i
modelli di deformabilità dei corpi per risolvere il problema.
PROCEDURA PER LA SOLUZIONE DI PROBLEMI DI EQUILIBRIO E DIAGRAMMI
DI CORPO LIBERO
1. Definire il sistema al quale applicare le
equazioni di equilibrio
2. Diagramma di corpo libero: isolare il
sistema da tutti gli altri corpi, sostituendo i
vincoli con le reazioni vincolari ed
indicando tutte le forze (e coppie) agenti sul
corpo. Es: la figura riporta il diagramma di
corpo libero del manovellismo in alto.
3. Confrontare il numero di incognite Nin con
il numero di equazioni disponibili Neq. Se
Nin > Neq si dovrà suddividere il sistema
negli elementi rigidi che lo compongono, e
costruire il diagramma di corpo libero per
ognuno di essi. Occorre prestare attenzione
alle forze interne: la forza applicata dal
primo corpo al secondo è uguale e contraria
alla forza applicata dal secondo al primo
4. Scrivere per ciascun elemento le equazioni
di equilibrio. Se il sistema non è iperstatico
si avrà Nin = Neq
5. Verificare che il sistema di forze ottenuto
come soluzione del sistema di equazioni
soddisfi le condizioni di equilibrio.
Considerando il manovellismo in figura,
dato il carico orizzontale P applicato in B
determinare la coppia C applicata in O
affinché il sistema sia in condizioni di
equilibrio statico, e le reazioni vincolari in O
e B.
Considerando il sistema complessivo si
avrebbe:
Incognite :
r r
r
C, R O , R B
ovvero
r
C, R Ox , R Oy , R By
Equilibrio alla traslazione orizzontale
R Ox − P = 0
Equilibrio alla traslazione verticale
R Oy + R By = 0
Equilibrio alla rotazione (intorno al punto O)
C - R By ⋅ BA cos β + AO cos ϑ = 0
4 incognite, 3 equazioni...il sistema non è risolvibile!
q
β
Incognite :
r r
r
r
C, R O , R B , R A
ovvero
r
r
C, R Ox , R Oy , R By , R Ax , R Ay
q
Equilibrio alla traslazione orizzontale
R Ox − R Ax = 0
(corpo 1)
R Ax − P = 0
(corpo 2)
Equilibrio alla traslazione verticale
R Oy − R Ay = 0
(corpo 1)
R Ay + R By = 0
(corpo 2)
Equilibrio alla rotazione
C - R Ax ⋅ AO sin ϑ + R Ay ⋅ AO cos ϑ = 0 (corpo 1, intorno a O)
R Ax ⋅ AB sin β + R Ay ⋅ AB cos β = 0
(corpo 2, intorno a B)
6 incognite, 6 equazioni...il sistema è risolvibil e
β
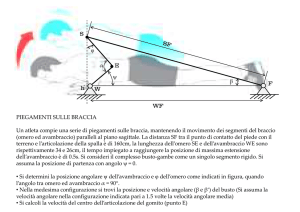
EQUILIBRIO STATICO: esempio
Muscoli flessori dell’avambraccio
strato superficiale:
bicipite brachiale
Origine scapola
(capo lungo,
tubercolo
sopraglenoideo –
capo breve,
processo
coracoideo)
Inserzione –
tuberosità del radio
strato profondo:
Brachiale
Origine: omero
(metà distale
diafisi)
Inserzione
(tuberosità
dell’ulna)
Considerando il braccio disposto
nella configurazione in figura, si
vuole determinare la forza Fm che
deve esprimere il bicipite brachiale
affinché il sistema sia in equilibrio
statico.
L = forza peso del corpo sorretto
dalla mano
W = forza peso del’avambraccio
applicato al baricentro
Equilibrio alla traslazione orizzontale
HC = 0
Equilibrio alla traslazione verticale
VC + Fm − W − L = 0
Equilibrio alla rotazione (intorno all' articolazione del gomito C)
Fm sinϑ ⋅ a − Wsinϑ ⋅ b − Lsinϑ ⋅ l = 0
Si trova
b
l
+L⋅
a
a
b
l
Vc = W ⋅ 1 − + L ⋅ 1 −
a
a
Fm = W ⋅