1
Esercizio
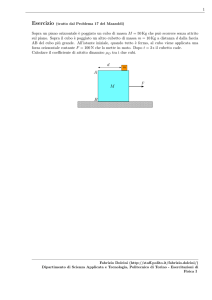
Un corpo di masssa m = 1.5 Kg sale lungo un piano inclinato (θ = 30o ) scabro (µD = 0.25),
partendo dalla base (punto A) con velocità v0 = 10 m/s e diretta parallelamente al piano
inclinato. Si osserva che il corpo, dopo aver raggiunto un’altezza massima hmax (punto B),
ridiscende indietro lungo il piano e ritorna in A.
1. Descrivere le forze che agiscono sul corpo, sia nel tratto A → B che nel tratto B → A;
2. Calcolare il lavoro compiuto sul corpo
(a) dalla forza peso;
(b) dalla forza di attrito;
(c) dalla reazione vincolare del piano
lungo il percorso chiuso A → B → A;
3. Calcolare la differenza tra l’energia cinetica iniziale (in A alla partenza) e quella finale
(in A al ritorno)
B
v0
hmax
A
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni
di Fisica I
2
SOLUZIONE
1. Durante i due tratti del percorso agiscono:
-forza peso
-forza di attrito dinamico
-reazione vincolare del piano
2. Calcoliamo ora il lavoro compiuto da ciascuna di tali forze nel percorso chiuso A →
B→A
(a) Lavoro della forza peso:
Nel primo tratto A → B lo spostamento d~s è diretto da A (s = 0) a B (s = d)
verso monte. La forza peso è diretta verso il basso e la sua componente nella
direzione di d~s è diretta verso valle (opposta al moto)
Z
B
d
Z
m~g · d~s =
(−mg sin θ) ds =
Z d
ds = −mg sin
= −mg sin θ
| {zθ d} =
A
0
0
=hmax
= −mghmax < 0
(1)
Nella secondo tratto B → A lo spostamento d~s è diretto da B (s = 0) a A
(s = d) verso valle. La forza peso è diretta verso il basso e la sua componente
nella direzione di d~s è ancora diretta verso valle (concorde al moto)
Z
A
Z
d
m~g · d~s =
(+mg sin θ) ds =
Z d
= mg sin θ
ds = mg sin
| {zθ d} =
B
0
0
=hmax
= = mghmax > 0
(2)
Quindi il lavoro nel percorso chiuso A → B → A vale
I
Wpeso =
Z
B
m~g · d~s =
Z
A
m~g · d~s +
A
m~g · d~s =
B
= −mg sin θ d + mg sin θ d = 0
(3)
(b) Lavoro della forza di attrito:
Nel primo tratto A → B lo spostamento d~s è diretto da A (s = 0) a B (s = d)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni
di Fisica I
3
verso monte e la forza di attrito è diretta verso valle (opposta al moto)
Z
B
d
Z
F~att · d~s =
(−µD mg cos θ) ds =
Z d
ds = −µD mg cos θ · |{z}
d =
= −µD mg cos θ
A
0
0
max
= hsin
θ
hmax
tan θ
= −µD mg
(4)
Nella secondo tratto B → A lo spostamento d~s è diretto da B (s = 0) a A (s = d)
verso valle e la forza di attrito è diretta verso monte (opposta al moto)
Z
A
F~att · d~s =
Z
d
(−µD mg cos θ) ds =
Z d
ds = −µD mg cos θ · |{z}
d =
= −µD mg cos θ
B
0
0
= −µD mg
max
= hsin
θ
hmax
tan θ
(5)
Quindi il lavoro nel percorso chiuso A → B → A vale
I
Watt =
F~att · d~s =
Z
B
F~att · d~s +
Z
A
A
B
2µD mghmax
<0
F~att · d~s = −
tan θ
(6)
(c) Lavoro della reazione vincolare del piano:
~ del piano è sempre diretta perpendicolarmente al piano,
La reazione vincolare R
e dunque è ortogonale alla direzione dello spostamento d~s. Quindi il lavoro nel
percorso chiuso A → B → A vale
I
WR =
~ · d~s =
R
Z
B
A
~ · d~s +
|R{z
}
=0
Z
A
B
~ · d~s = 0
R
| {z
}
(7)
=0
Osservazione:
Si noti la differenza tra la forza peso (conservativa) e la forza di attrito (non
conservativa). La forza peso è diretta sempre verso valle, e dunque il lavoro che
compie è negativo da A → B (forza discorde al moto) e positivo da B → A (forza
concorde al moto). Quindi nel percorso chiouso i due contributi si cancellano l’uno
con l’altro (=il lavoro di una forza conservativa in un percorso chiuso è nullo).
Al contrario, la forza di attrito si oppone sempre al moto, e dunque il lavoro che
compie è negativo sia da A → B che da B → A, dando un lavoro totale non nullo
sul percorso chiuso.
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni
di Fisica I
4
3. Per trovare la variazione di energia cinetica applichiamo il teorema dell’energia cinetica
al percorso chiuso A → B → A
∆K
|{z}
K(A0 )−K(A)
= Wpeso +
| {z }
=0
Watt
|{z}
=−
2µD mghmax
tan θ
+ WR
|{z}
(8)
=0
dove A0 denota il punto A nell’istante in cui il corpo ci ritorna scendendo. Otteniamo
dunque
2µD mghmax
K(A0 ) − K(A) = −
<0
(9)
tan θ
Per valutare esplicitamente la variazione dobbiamo calcolare hmax . A tale scopo applichiamo il teorema dell’energia cinetica al primo tratto A → B
∆K
|{z}
=
K(B)−K(A)
Wpeso +
| {z }
=−mghmax
Watt
|{z}
=−
µD mghmax
tan θ
+ WR
|{z}
=0
⇓
1 2
µD 0 − mv0 = −mghmax 1 +
2
tan θ
da cui
hmax =
v02
µD
2g 1 + tan
θ
(10)
Sostituendo (10) in (9) otteniamo
K(A0 ) − K(A) = −
mµD v02
tan θ + µD
(11)
Sostituendo i valori
1.5 Kg · 0.25 · (10 ms )2
K(A ) − K(A) = −
=
tan π6 + 0.25
1.5 · 25
m2
= −
Kg 2 = −45.3 J
0.577 + 0.25 | {zs }
0
(12)
=J
Osservazione:
La variazione di energia cinetica è negativa: quando il corpo ritorna in A la sua energia
cinetica è minore di quella con cui era partito da A, a causa del lavoro compiuto dalla
forza di attrito durante il percorso chiuso, che ha sottratto energia meccanica al corpo.
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni
di Fisica I