UNIVERSITÀ di ROMA TOR VERGATA - Dipartimento di Matematica

UNIVERSITÀ di ROMA TOR VERGATA
Corso di Laurea in Matematica
Corso di PS2-Probabilità 2
P.Baldi
Tutorato 11, 30 maggio 2012
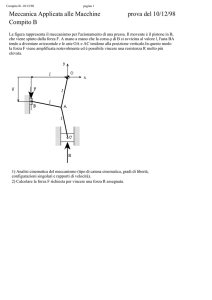
Esercizio 1 Consideriamo la catena di Markov sui vertici del grafo della Figura 0.1. Ad
ogni transizione la catena si sposta dalla posizione in cui si trova ad uno dei vertici contigui,
scelto a caso.
a) Qual è la distribuzione invariante di questa catena ? È unica ? Si tratta di una catena
regolare ?
b) Cosa cambia se invece la catena fosse modificata in modo che se i è uno degli stati
5, 6, 7, 8, 9, 10 la catena possa con probabilità 21 restare in i e con probabilità 21 spostarsi
nello stato adiacente ?
c) Quanto tempo in media occorre per giungere in uno degli stati 5, . . . , 10 partendo
da 1 ?
6•............
7
5
..
....•
.......
.......
....... ............
.•
....
..
..
..
..
..
..
...
.
.
..
.
•
•.............
.
.
.
... .............
.......•
.
.
.
.
.......
.
....... ............
...................
...........
.
.
•...
•...
...
...
...
...
...
...
...
...
...
•
•...
2
1
3
8
10
4
9
Figura 0.1
Esercizio 2 Due giocatori A e B giocano lanciando ripetutamente una moneta che dà testa
con probabilità p e croce con probabilità 1 − p. La regola è che A vince non appena escono
due teste consecutive, mentre B vince non appena escono due croci consecutive.
a) Modellizzare questo gioco con una opportuna catena di Markov.
b) Qual è la probabilità che vinca il giocatore A ?
c) Supponiamo p = 43 . Il giocatore A propone a B, come compensazione, che in
caso lui vinca B gli dia 1 euro, mentre se sarà B a vincere lui gli darà 9 euro, dato che
la probabilità di fare due teste consecutive è uguale a 9 volte la probabilità di fare 2 croci
consecutive. Vi sembra giusto ? Perché B è così arrabbiato ? Quanto dovrebbe ricevere B
da A perché il gioco risulti equilibrato ?
d) In media quanti lanci occorre fare in una partita ?
Esercizio 3 N palline vengono ripartite in due scatole. Ad ogni unità di tempo una delle
palline viene scelta a caso e quindi
• con probabilità p viene lasciata dov’è.
• con probabilità 1 − p, 0 < p ≤ 1, viene spostata dalla scatola in cui si trova all’altra.
Indichiamo con Xn il numero di palline presenti nella prima scatola.
a) Modellizzare questa dinamica con una catena di Markov di cui si daranno le probabilità di transizione.
b) Al variare di p, 0 ≤ p ≤ 1, si tratta di una catena irriducibile ? Regolare ?
c) Determinare le probabilità invarianti della catena. Supponiamo che al tempo 0 nella
scatola ci sia una pallina e p = 21 , quanto vale, approssimativamente la probabilità che al
tempo n la scatola sia vuota, per n grande ?
Soluzioni
Esercizio 1 a) Tutti gli stati comunicano tra loro, perché il grafo è connesso; dunque la catena
è irriducibile e la distribuzione stazionaria è unica. Per calcolarla ci sono due possibilità: la
prima consiste nel risolvere il sistema lineare πP = π più la condizione π1 +. . .+π10 = 1.
Non è una via troppo complicata perché per motivi di simmetria è chiaro che deve essere
π2 = π3 = π4 e π5 = π6 = π7 = π8 = π9 = π10 . Ci si riconduce quindi a un sistema
lineare in tre incognite.
La seconda consiste nel ricordare che per una catena di Markov sui vertici di un grafo c’è
una formula esplicita della distribuzione stazionaria: se ki è il numero di spigoli del grafo
che arrivano nel vertice i e k è la somma dei numeri ki , allora
πi =
ki
k
è la distribuzione invariante. Qui ki è uguale a 3 per 4 vertici e uguale a 1 per 6. Dunque
1
k = 18. La distribuzione invariante vale 16 per gli stati 1, 2, 3, 4 e 18
per gli altri.
La catena non è regolare. Basta osservare che gli stati si possono suddividere in due
classi: la prima formata da 1, 5, 6, 7, 8, 9, 10 e la seconda da 2, 3, 4. Se la catena si trova in
uno stato della prima classe, all’istante successivo si troverà in uno della seconda e viceversa.
Non è dunque possibile che esista n tale che, partendo da i, si possa essere in ognuno degli
stati con probabilità positiva.
b) Con le nuove regole di transizione la catena è ora regolare: essa è infatti ancora
irriducibile e per di più pii = 21 per gli stati da 5 a 10. Vi sono dunque degli elementi > 0
sulla diagonale della matrice di transizione e questo, insieme alla irriducibilità, assicura la
regolarità della catena. Anche qui possiamo, a scelta, risolvere il sistema della stazionarietà
oppure ricorrere alla formula delle probabilità invarianti per le passeggiate aleatorie sui
vertici di un grafo (con gli stati 5, . . . , 10 che sono connessi a loro stessi da un arco). Il
sistema lineare della probabilità stazionaria è
v 1 = v2
(1)
v2 =
1
3
v1 + v3
v1 + 3v2 + 6v3 = 1
dove indichiamo con v1 il valore della probabilità stazionaria nello stato 1, con v2 quello
negli stati 2, 3, 4 e con v3 quello negli stati ‘‘esterni’’. Con la formula dei grafi, invece, la
somma degli archi dà ora k = 24 e quindi
πi =
1
8
1
12
se i = 1, 2, 3, 4
se i = 5, . . . , 10 .
e si verifica facilmente che questi numeri danno la soluzione di (1).
c) Il tempo medio di passaggio nella classe {5, . . . , 10} partendo da i, i = 1, 2, 3, 4,
indicato ζi , si ottiene risolvendo il sistema
ζi = 1 +
4
X
pij ζj ,
i = 1, 2, 3, 4 .
j =1
Questo si risolve facilmente osservando che, per motivi di simmetria, deve essere ζ2 = ζ3 =
ζ4 . Giungiamo quindi al sistema
ζ2 = 1 + 13 ζ1
ζ1 = 1 + ζ2
che dà facilmente ζ1 = 3, ζ2 = 2. Partendo da 1 dunque si giunge in uno degli stati
5, . . . , 10 in media in 3 passi.
Esercizio 2 a) Possiamo considerare una catena di Markov sull’insieme di stati seguente
1 →stato iniziale,
2 →l’ultimo lancio ha dato testa, ma non il penultimo,
3 →l’ultimo lancio ha dato croce, ma non il penultimo,
4 →A vince,
5 →B vince,
Date le regole del gioco, a partire dallo stato iniziale la catena si sposterà in 2 con
probabilità p e in 3 con probabilità q. Se si è in 2 invece A vincerà se il lancio darà ancora
T (probabilità p), mentre se darà croce la catena si posterà sullo stato 3. Con questo tipo di
considerazioni si vede che la matrice di transizione è
1
1 0
2
0
3
0
40
5 0

2
p
0
p
0
0
3
q
q
0
0
0
4
0
p
0
1
0
5

0
0

q

0
1
b) Si tratta di calcolare la probabilità di passaggio in 4 partendo da 1. Il sistema da
risolvere qui diventa
λ1 = pλ2 + qλ3
λ2 = p + qλ3
λ3 = pλ2 .
Sostituendo il valore di λ3 dato dalla terza equazione nella seconda si trova λ2 = p + qpλ2 ,
da cui si calcola immediatamente λ2 e quindi quelli di λ1 e λ3 :
1+q
,
λ1 = p
1 − qp
2
p
,
λ2 =
1 − qp
p2
λ3 =
·
1 − qp
Si ricorda che la probabilità che sia il giocatore A a vincere è λ1 .
c) Se p = 43 , q = 41 , allora la probabilità, pA , che il giocatore A vinca si ottiene
sostituendo questi valori nell’espressione di λ1 ottenuta sopra:
pA =
9
16
5
4
1−
3
16
=
45
52 ·
mentre la probabilità che sia il giocatore B a vincere sarà evidentemente pB = 1−pA =
In media quindi il giocatore B guadagna, in media,
9 · pB − 1 · pA =
18
52
7
52 .
>0
Il giocatore B ha torto di essere arrabbiato, A si è fatto male i conti. . .
d) Si tratta di calcolare il tempo medio di passaggio nella classe chiusa degli stati
ricorrenti {4, 5}. Il sistema da risolvere è
ζ1 = 1 + pζ2 + qζ3
ζ2 = 1 + qζ3
ζ3 = 1 + pζ2
Di nuovo sostituendo il valore di ζ3 , si trova
ζ2 = 1 + q(1 + pζ2 ) = 1 + q + qpζ2
da cui si ricava il valore di ζ2 e poi tutti gli altri:
ζ2 =
Con i valori p = 43 , q =
1+q
,
1 − qp
1
4
ζ3 =
1+p
,
1 − qp
ζ1 =
2 + qp
·
1 − qp
del punto d), il tempo medio del gioco è
ζ1 =
2+
1−
3
16
3
16
=
35
13 ·
Esercizio 3 a) Se Xn = k, ciò significa che nella prima scatola ci sono k palline e conseguentemente ce ne sono N − k nell’altra scatola. Quando si sceglie una pallina, questa
si troverà nella prima scatola con probabilità Nk e nella seconda con probabilità 1 − Nk .
Dunque, se Xn = k, al tempo n + 1 nell’urna vi saranno
• ancora k palline con probabilità p;
• k − 1 palline con probabilità (1 − p) Nk ;
• k + 1 palline con probabilità (1 − p)(1 − Nk ).
Si tratta dunque di una catena di nascita e morte su E = {0, 1, . . . , N } con
pk = pk,k+1 = (1 − p)(1 −
k
N)
rk = pk,k = p
qk = pk,k−1 = (1 − p) Nk ·
per k = 0, 1, . . . , N .
b) Se p < 1, cioè 1 − p > 0, allora si ha pk > 0 per ogni k = 0, . . . , N − 1. Cioè
ogni stato comunica con tutti gli stati alla sua destra. Per lo stesso motivo, qk > 0 per ogni
k = 1, . . . , N e dunque ogni stato comunica con ogni stato alla sua sinistra. La catena è
dunque irriducibile. Se invece p = 1, allora tutti gli stati sono assorbenti e non comunicano
tra loro.
Se p > 0, allora rk = p > 0 e dunque sulla diagonale della matrice di transizione ci
sono degli elementi > 0 (tutti, in particolare). Dunque la catena è anche regolare. Se invece
p = 0, allora sulla diagonale ci sono solo zeri e non si può applicare il criterio. Si vede
anzi facilmente che in questo la catena non è regolare e che che si possono suddividere gli
stati in due classi in modo che ad ogni transizione si passa dall’una all’altra. Del resto per
p = 0 questa catena non è altro che il modello di Ehrenfest (Esercizio 5.12).
c) Per calcolare la distribuzione stazionaria si possono usare le formule che si sono
viste per le catene di nascita e morte. Qui, con le notazioni dell’Esempio ‘mk.117’,
1 · (1 − N1 ) . . . (1 − i−1
p0 . . . pi−1
N(N − 1) . . . (N − i + 1)
N
N )
=
=
.
ξi =
=
1
i
i
q1 . . . qi
1...i
N ... N
Ricordiamo che la distribuzione stazionaria è data da
ξi
πi = PN
·
h=0 ξh
Ricordando che
N X
N
= 2N
−N
N
i
h=0
i
troviamo dunque
πi = 2
risultato identico a quello che si ottiene per il modello di Ehrenfest. In particolare la
distribuzione stazionaria non dipende da p (purché p < 1 naturalmente).
Per p = 21 abbiamo visto che la catena è regolare (a differenza dal modello di Ehrenfest).
Dunque per n grande la probabilità che la prima scatola sia vuota è approssimativamente
uguale a π0 = 2−N N0 = 2−N (qualunque sia il numero si palline nella scatola all’inizio).