Compito B -10/12/98
pagina 1
Meccanica Applicata alle Macchine
Compito B
prova del 10/12/98
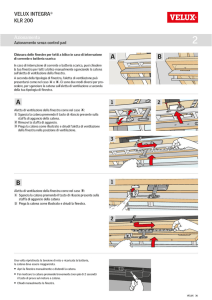
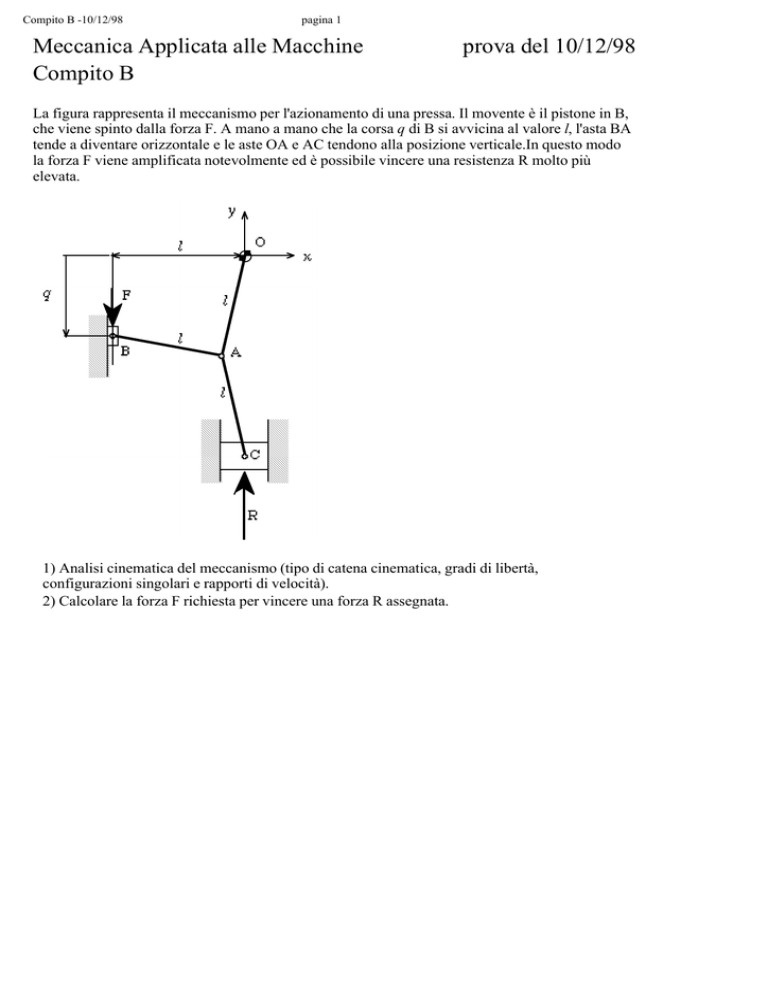
La figura rappresenta il meccanismo per l'azionamento di una pressa. Il movente è il pistone in B,
che viene spinto dalla forza F. A mano a mano che la corsa q di B si avvicina al valore l, l'asta BA
tende a diventare orizzontale e le aste OA e AC tendono alla posizione verticale.In questo modo
la forza F viene amplificata notevolmente ed è possibile vincere una resistenza R molto più
elevata.
1) Analisi cinematica del meccanismo (tipo di catena cinematica, gradi di libertà,
configurazioni singolari e rapporti di velocità).
2) Calcolare la forza F richiesta per vincere una forza R assegnata.
Compito B -10/12/98
pagina 2
Analisi cinematica.
Il meccanismo è un esalatero di watt (se si considera BA collegata a OA). In A ci
sono due coppie rotoidali sovrapposte. ovviamente si ha un grado di libertà.
Per scrivere le equazioni di chiusura conviene considerare il punto D del telaio
indicato nella figura seguente:
I poligoni di chiusura sono ODBAO e OACO (BA = Z1, AO = Z2,CA =Z3).
l
−l
cos π
sin π
+q
cos θ 2
sin θ 2
−l
cos 3 π
sin
2
3π
2
cos θ 3
sin θ 3
+l
−
cos θ 1
sin θ 1
0
y
+l
= 0
0
l cos θ 2 + l cos θ 1 − l = 0
l sin θ 2 + l sin θ 1 − q = 0
− l cos θ 3 − l cos θ 2 = 0
− l sin θ 3 − l sin θ 2 − y = 0
l'analisi di velocità per la prima catena fornisce:
− l sin θ 1 θ' 1 − l sin θ 2 θ' 2 = 0
l cos θ 1 θ' 1 + l cos θ 2 θ' 2 = q'
che risolta da:
cos θ 2
sin θ 2
= 0
0
Compito B -10/12/98
pagina 3
sin θ 2
θ' 1 = 1
q'
l sin θ 2 − θ 1
sin θ 1
θ' 2 = − 1
q'
l sin θ 2 − θ 1
dove sono evidenti i rapporti di velocità.
Inoltre la configurazione singolare richiede che il denominatore sia nullo:
sin θ 2 − θ 1 = 0
che richiede che le aste Z1 (BA) e Z2 (AO) siano allineate o anti - allineate. Si può
verificare che la seconda condizione non si realizza mai, mentre la prima si
realizza quando:
θ1 = θ2
che sostituita nelle equazioni di chiusura fornisce:
l sin θ 2 + l sin θ 2 − q = 0
l cos θ 2 + l cos θ 2 − l = 0
ovvero:
cos θ 2 =
1
2
a cui corrispondono due casi:
θ2 = 1π
θ2 = −1π
q = 3l
q =− 3l
3
3
L'analisi di velocità della seconda catena si fa con θ2 considerato movente.
− l cos θ 3 θ' 3 − y' = l θ' 2 cos θ 2
l sin θ 3 θ' 3 = − l sin θ 2 θ' 2
si ottiene:
sin θ 2
θ'
sin θ 3 2
sin θ 3 − θ 2
y' = − l
θ' 2
sin θ 3
θ' 3 = −
La singolarità per la seconda catena si realizza se θ3 è nullo, che si realizzerebbe se
C venisse a sovrapporsi a O.
Equilibrio delle forze.
Si calcola con il principio dei lavori virtuali:
Compito B -10/12/98
pagina 4
F δq + R δy = 0
esprimendo y in funzione di q e del relativo del rapporto di velocità:
δy = τ yq δq
che fornisce:
F = − τ yq R
Il rapporto di velocità è il prodotto dei due rapporti q - θ2 - y appena trovati:
τ yq =
y'
q'
−l
τ yq =
τ yq
sin θ 3 − θ 2
θ' 2
sin θ 3
q'
sin θ 3 − θ 2 sin θ 1
=
sin θ 2 − θ 1 sin θ 3
3) Procedura per l'analisi di posizione del quadrilatero.