Document

Analisi di Buckling
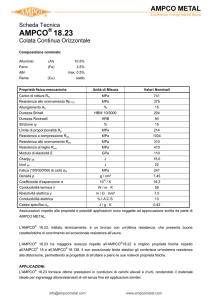
Come detto in precedenza esistono due procedure attivabili per il calcolo dei carichi di collasso
La prima si basa sulla ricerca del punto di biforcazione mediante l’analisi modale
La seconda utilizza il calcolo non lineare e determina il carico di collasso direttamente
valutando il valore massimo raggiungibile fino ad un cambio drastico di configurazione
deformata
Fc
Metodo non lineare: si opera in controllo di
carico (carico crescente) e il calcolo non
converge più a Fc
Oppure in controllo di deformazione e si
esamina l’intera curva di risposta
Calcolo autovalori determinando il punto di
biforcazione (come si vede il calcolo non è in
sicurezza in quanto si linearizza il
comportamento fino al punto di collasso)
Impostazione agli autovalori
Il problema si risolve mediante un’analisi agli autovalori delle matrici
K elast   K*geom  0
È quindi necessaria un’analisi preventiva statica non lineare che consente di calcolare la
K*geom (opzione di stress stiffening)
Viene di seguito presentato come si forma tale matrice in una trave in flessione
P
P
u
v
Per piccoli spostamenti, si può scrivere l’equazione di equilibrio dei momenti attorno al punto di
sinistra
2
dx 

dM 
dT



 dv 
M M 
dx   q
 T 
dx  dx  P   dx  0
dx
2
dx




 dx 
Eliminando i termini in
dx2
, e derivando rispetto ad x:
d 2 M dT
d2v

P 2 0
2
dx
dx
dx
d2v
M  E I 2
dx
Non considerando le deformazioni a
taglio si ha dalla teoria della trave
d4v
d2v
EI 4 P 2 q
dx
dx
dT
 q
dx
Che è la classica equazione differenziale dalla quale si può
dedurre l’instabilità delle colonne, valida per ogni C.C.
v  x   C1 sin kx  C2 cos kx  C3 x  C4
+
Condizioni al Contorno
Si può ora applicare la formulazione debole per la determinazione delle matrici di
rigidezza a partire dalla formulazione della deformazione troncata al II ordine
(termine flessionale) (grandi deformaz.)
2
2
2
u 1  u   v   w  
 xx 
       
 
x 2  x   x   x  
Energia di deformazione:
1
U 
2L
U
 d 2 v  1  dv 
du
 xx 
 y  2    
dx
 dx  2  dx 
1
E  2xx dV

2 Ve
2
Sostituendo e svolgendo prodotti
2
4
2
2
2
2
  du 2
 d 2 v   dv   du  dv  
1  dv 
 du   d v 
2d v
  E dA dx
A  A  dx   y  dx2   4  dx   2 y  dx   dx2   y  dx2   dx    dx 
dx
  

 dA  0
Il precedente integrale si può ridurre ad un integrale
di linea ricordando le proprietà delle sezioni:
A
2
4
  du 2
 d 2v  A  dv 
1
U   E  A   I  2  
  A
2 L   dx 
dx
4
 dx 



;
 y dA  0
A
 du   dv 
   
 dx   dx 
;
 y dA  I
2
A
2

 dx

4
Trascurando il termine di potenza più alta
E ricordando che
PE A
1
A  dv 
E
  dx  0

2L
4  dx 
du
dx
Si perviene alla seguente
espressione della energia elastica
2
2
2
 d 2v 
1   du 
 dv  
U    EA    EI  2   Px    dx
2 L   dx 
 dx  
 dx 

L’energia elastica è suddivisibile in due componenti, il primo associato a deformazioni
assiali e il secondo a deformazioni flessionali
2
U  U ax  U fl
1
 du 
U ax   EA   dx
2L
 dx 
2
2
 d 2v 
1 
 dv  
U fl    EI  2   Px    dx
2L
 dx  
 dx 

Nel problema discretizzato si può esprimere lo spostamento mediante le funzioni di forma, per
cui l’energia totale diviene:
2
2
 d2v 
1 L
 du 
U   E A   E I  2   P
2 0
 dx 
 dx 

1
 fax
2
T

 UW
 dv 
    N1 , x  f fl
 dx 
 N1 , x 
 N11
1
 f fl
2
 K ax   fax 
N12,x
1
 fall
2

T
K fl 
 f fl
2

 dx

1
 f fl
2

 K   fall    f fl 
2
1
T
K g   P K*g 
N13
 dv 
 
 dx 
T
K*g  
K g 

T
fl
T
fl
0 N1 , x  N1 , x
L
f 
 f   f   P 
T
all
A dx

x2
x3
x 2 x3
x2
x3
x 2 x3 
N14  , x  1  3 2  2 3 , x  2  2 , 3 2  2 3 ,   2 
L L
L L , x
L
L
L
L

Derivando le precedenti si ha:
 N1 , x  
K g 
6
x
4
x

12
,


6
,
2
3
2
L
L
L
 L
6
x
2
x

12
,


6
L
L2
L3
L2 
Per ricavare K *g  non resta che risolvere l’integrale
x
 6


12
 L2
L3 


4
x
  6

2
L
x
L   6
K *g     L
   2  12 3

0
L
 6  12 x   L
2
3
L
L 
 2
x 
  6 2 
L 
 L
v1
 6
 5L

 1

K *g    10
 6
 5L
 1

 10
1

v2
1
6

10
5L
2
1
L 
15
10
1
6

10 5 L
L
1


30
10
4
x
6 2
L
L
6
x

12
L2
L3
2
1 
10 

L

30 

1

10 
2 
L
15 
v1
1
v2
2
Si noti che sono presenti solo gdl flessionali

2
x 
 6 2  Adx
L
L 
Soluzione non lineare
Esistono due modalità di evoluzione non lineare, la prima facendo crescere il carico e la
seconda lo spostamento
In realtà ne esiste anche una terza, combinazione delle due precedenti, che prende il
nome di Arch-length od analisi di Riks
Il calcolo non lineare si
muove su questo arco
Il calcolo a collasso non lineare è a tutti gli effetti un’analisi non lineare tout court e
quindi si rimanda l’approfondimento a quello del calcolo non lineare in genere
Risoluzione di problemi strutturali non lineari
Dal punto di vista strutturale, i problemi sono non lineari se, nota la risposta del sistema ad un
determinato livello di carico, incrementando tale livello i risultati non sono proporzionali
all’incremento stesso
Se chiamiamo step l’intera soluzione, dal momento in cui non è applicato il carico al suo valore
finale, è quasi sempre necessario suddividere lo step in un certo numero di substep, ove si
imponga la soddisfazione dell’equilibrio (forze residue piccole)
Anche all’interno dei substep il calcolo è non lineare, quindi sarà necessario operare un certo
numero di iterazioni all’interno (ciascuna costituita da un calcolo lineare) finché non si avrà al
corrispondente substep una soluzione con forze residue minori del voluto
risposta
iterazioni
tempo
Substeps
STEP
In ogni caso, il calcolo non lineare si sviluppa come un’analisi incrementale, del tipo:
1) In controllo di carico – i carichi sono applicati con una legge preimpostata
2) In controllo di spostamento – spostamenti imposti indipendentemente dalla risposta sistema
3) Controllo indiretto sulla risposta – controllo basato su combinazioni della risposta, come ad
esempio spostamenti relativi tra gdl
3) Controllo di tipo Arc length – si realizza mediante una combinazione di spostamento e carico
applicato la cui combinazione deve muoversi entro un raggio funzionale delle due grandezze
Il modello costitutivo del materiale fa ricorso alla matrice di rigidezza tangente del materiale
σ  ε  ε   σ  ε  
σ
ε 
ε ε=ε
D*  ε  
σ
ε ε=ε
Attraverso la quale si calcola la matrice di rigidezza tangente di ogni elemento della struttura
KT 
T
T σ ε
T
fint


B
σ
d


B
d


B
D*B d 



u u 
ε u


Per semplificare la trattazione, si espone la procedura per un sistema a risposta non lineare
che però possiede un solo grado di libertà
Il metodo di Newton-Raphson o
della rigidezza tangenziale ricerca la
soluzione dall’inizio di un substep
alla sua fine calcolando ad ogni
iterazione la matrice tangente ed
estrapolando su di essa
1) l’incremento di carico imposto
1
definisce il valore del residuo iniziale Rn  Pn
2) dal substep precedente è nota
u1n  ulast
n 1
3) Si determina la nuova matrice
K 1T
di rigidezza
4) Si calcola per estrapolazione
1
1
lineare l’incremento spostamento un   K TAN

5) Si trova
u2n  u1n  u1n
6) Si determinano le forze interne, si
calcola il nuovo residuo associato allo
spostamento estrapolato

1
1
n
R
fint
 2
 Rn
 2
K T
u3  u 2  u 2
 n1
n
n
7) . . . Si prosegue finché il
residuo risulta essere più grande
di un valore considerato
accettabile
8) Fine del substep con soluzione
convergente e pronti ad un nuovo
incremento del carico u1n1  ulast
n
Il metodo di Newton-Raphson modificato differisce dal precedente in quanto non si ricalcola la
matrice tangente ad ogni iterazione ma si utilizza quella relativa alla fine del substep precedente
Il metodo di Newton Raphson può
entrare in crisi se la struttura è hardening
- la convergenza diviene lentissima
P
Miglior tendenza con N.R.
modificato
P
x0
x4x3x2x1
Se il sistema ha comportamento non monotono si
può mancare totalmente la convergenza anche col
metodo non modificato
Caso di sistema hardening
Convergenza lenta con NewtonRaphson
Non convergenza con NewtonRaphson modificato
Nel metodo della secante si effettua una prima iterazione secondo il metodo classico di NewtonRaphson e poi si determina la matrice secante mediante
2
du1n   K1SEC
   Rn1  Rn2 
1
La determinazione della matrice secante è immediata in un problema scalare, come
quello rappresentato in figura, ma molto meno banale per rigidezze matriciali
Esiste anche un metodo della secante modificato (Iterazione diretta di Picard) secondo il quale la
secante è computata sempre considerando la soluzione iniziale
Il miglior funzionamento delle varianti presentate dipende … dal problema stesso, e quindi è
di difficile determinazione aprioristica
L’adaptive descent può fare uso di due matrici di rigidezza incrementali, una è la matrice
tangente Kt e l’altra la matrice secante Ks
La matrice in uso è definita dalla espressione
K   K s  1   K t
L’iterazione ha inizio con  = 0, se la convergenza è difficile da raggiungere si fa crescere
 in modo da avvicinarsi alla matrice secante, più rigida se il sistema è hardening
Se nell’iterazione il residuo cresce (tendenziale divergenza):
Si porta ξ = 1 e si continua ad iterare così
Se nell’iterazione il residuo decresce (tendenziale convergenza):
Si riduce progressivamente ξ da 1 fino a riportarlo a 0 (matrice tangente)
Se durante l’iterazione si verifica un pivot negativo (matrice mal condizionata):
Si riduce riutilizza la matrice secante (ξ = 1) ed eventualmente si riduce la
dimensione del substep di avanzamento
Il line search è un metodo che prova a determinare la soluzione della iterazione modificando
i salti calcolati da Newton Raphson con l’adozione di un coefficiente sk appropriato
uin1  uin  sk  uin
con
s0  1.0
Noto il valore di sk si associa ad esso uno scalare che indica l’energia coinvolta nell’iterazione
gk   uin   Rin1,k
T
Ove naturalmente il residuo è calcolato dall’equilibrio delle forze esterne ed interne
Rin1,k  f ext  f int  uin1,k 
A questo punto si determina la nuova approssimazione di
sk+1 estrapolando verso g=0 la retta indicata nella figura
sk 1 
g0
g0
sk
g0  g k
Il processo termina dopo un numero prefissato di
iterazioni (e.g. 5) oppure quando si verifica una delle due
g0
 0.5
gk
g
gk  gk 1
 err
gk
gk
s
sk
sk 1
A seconda del metodo adottato, si realizzano perdite di convergenza diverse
L’arc length è un metodo molto adatto quando i sistemi sono softening-hardening, per esempio
nelle condizioni di post-buckling
Il metodo non è invece adatto nei sistemi ove discontinuità di carico si realizzano
frequentemente durante gli step di carico (analisi con contatti tra superfici, …)
La curva degli equilibri successivi in pratica si determina da una combinazione sia degli
spostamenti delle variabili incognite, sia del fattore scalare di carico che agisce su tutti i carichi
applicati
Dato però che spostamenti e forze applicate sono dimensionalmente differenti, occorre definire
una costante di comparazione c:
l  u  u   c 
T
2
Per gli elementi in cui sono presenti sia gdl
traslazionali che rotazionali si introducono
anche altri fattori di comparazione
In un substep, si parte da un1 , n1
un , n
e si vuole determinare i nuovi
In pratica si ha una nuovo parametro n con la condizione vincolare sulla lunghezza di l
Riscriviamo la linearizzazione dell’equilibrio della generica iterazione i :
f
0
i 1
i 1
i
 ni 1f  ni f   fint,
n  K n  un  0
i 1
i
K in1 uin  f0  ni 1f  fint,
n  n f
INCOGNITE
Ora, pensando che una iterazione porta da una soluzione  uin1 = u0 ad una  u f possiamo
linearizzando imporre l’equilibrio nella condizione iniziale (0) e finale (f)
Esprimendo la
variazione di
spostamento come
Si separa
l’equazione
precedente in due
 uin   u0  ni  u f
Sia  u0 che  u f sono note e quindi, sostituendo nella
 u
i 1
n
  u
i T
n
u
i 1
n
  u   c  
i
n
2
i 1
n
 
i
n
  l
i 1
i 1
i 1

K n  u0  f0  n f  fint, n
 i 1

K n  u f  f
l’unica incognita presente è ni
2
Il sistema, di II grado, fornisce due
soluzioni: una avanza nel percorso,
l’altra retrocede
Per quanto riguarda i criteri di convergenza essi possono essere basati sia sulle forze
(e momenti) residui sia sullo spostamento della soluzione dall’iterazione precedente
I primi sono senz’altro da preferire in quanto hanno un preciso significato fisico, i secondi
invece possono mascherare enormi errori nell’equilibrio per strutture particolarmente rigide
Infine, in genere i codici controllano se da una iterazione alla successiva si ha una nuova
condizione di contatto ed in tale caso effettuano sempre una iterazione aggiuntiva,
fermandosi quando non si altera più il quadro complessivo dei contatti
La ricerca della soluzione può anche diventare estremamente difficile quando sono presenti
condizioni non continue, come contatto o bruschi cambi di pendenza curva plastica del
materiale, passaggi di stato, ...
In particolare i problemi di contatto, peggio se associati a plasticità che invece produce
softening sono spesso difficoltosi perché instaurano delle condizioni di hardening
all’insorgere della penetrazione sul target
Comportamento plastico dei materiali (metallici)

La plasticità è caratterizzata da una correlazione non
biunivoca tra il valore della deformazione accumulata e
quello della tensione, in pratica si può vedere se in un ciclo
di carico e scarico si ripercorre o no il medesimo percorso
carico
scarico


Nei materiali elasto-plastici perfetti esiste un valore di
tensione di yield oltre il quale le deformazioni sono
indeterminate
y

I materiali che incrudiscono sono invece caratterizzati
da un valore di yielding che dipende da qualche
parametro di controllo 
L’equazione della superficie di Yield è
Nei materiali che presentano incrudimento la superficie
tende ad espandersi mano a mano che si accumula
plasticità
Il più accreditato è la
deformazione plastica
Fσ,   0
2

1
Analisi del flusso plastico
Nel caso di presenza di flusso plastico il materiale è caratterizzato da un legame tensione –
deformazione che si modifica durante l’evento plastico.
In una semplificazione comunemente adottata, il materiale all’interno di una superficie di
snervamento si comporta elasticamente, al di fuori plasticizza
Se incrudente, si ha una estensione della superficie di snervamento stessa determinata dall’entità
della deformazione plastica stessa.
Chiamando con F la superficie di snervamento, essa sarà funzione dello stato di tensione e di un
parametro  che tiene in conto dell’incrudimento subito
F  σ,    0
(1)
Il tensore delle tensioni è naturalmente il seguente:
 xx  xy  xz 


σ   xy  yy  yz 
  xz  yz  xx 


Considerando la tensione media, si può scrivere un tensore
deviatorico che si costruisce eliminando la componente idrostatica:
 xx   m
 xy
 xz 


s    xy
 yy   m
 yz 
  xz
 yz
 xx   m 

 m  1 3  x   y   z 
Si rammentano anche i tre invarianti delle tensioni che sono così definiti, una volta che è stato
individuato il sistema di riferimento principale
I1  σ   1   2   3
I3  σ   1 2 3
I 2  σ    1 2   2 3   3 1
Nel caso si faccia uso del tensore deviatorico, i tre invarianti assumono i valori
1
2
2
2
J 2  σ    1   2    2   3    3   1  

6
J1  σ   0
J 3  σ   s1s2 s3
Il criterio di snervamento di Von Mises è imediatamente legato a J2
 eq 
1
2
1   2    2   3    3  1 
2
2
2
 eq  3 J 2  σ 
Qualora ci si trovasse in un sistema di riferimento non principale, il J2 diverrebbe
J2 σ  
2
2
1
2
2
2
2 












6













x
y
y
z
z
x
xy
yz
zx
6 
La deformazione plastica equivalente viene anche essa in
genere conteggiata mediante un criterio alla Von Mises
 eqpl  3 J 2  ε pl  
3 pl pl
 ij   ij
2
Un metodo per determinare le direzioni principali
deviatoriche, alternativo alla soluzione del
;
problema agli autovalori, è dato dalle seguenti
; espressioni (Kachanov):
;
2
1 

s1 
J 2 cos     
3 
3

Avendo posto
2 ;
1 

s2 
J 2 cos     
3 
3

 cos 3 
s3 
2
J 2 cos    
3
3 3 J3
2  J2 
A questo punto le tensioni principali altro non sono che
3
2
1  s1   m
 2  s2   m
 3  s3   m
Tornando alla superficie di yielding F, se si adotta la tensione equivalente di Von Mises, l’eq (1) è
F  σ,     eq   y    0
1
2
2
2
2
1   2    2   3    3  1    y    0
Incrudimento isotropico
In questa ultima equazione l’effetto dell’incrudimento viene conteggiato mediante la variazione
della tensione di snervamento, che sarà funzione di un parametro  da definire ma che tiene in
considerazione il livello di plasticità raggiunto
Superficie di snervamento
La superficie di snervamento definisce l’innesco della condizione di plasticità
L’estensione di tale superficie si attualizza con la deformazione plastica accumulata
F  σ, ε pl   0
Materiale Elasto-Plastico perfetto
In questo caso la condizione di plasticizzazione è totalmente indipendente
dalla deformazione plastica
F σ  0
La condizione di plasticizzazione rimane la stessa nel corso della deformazione plastica, sia nella
estensione che nella posizione originaria
Incrudimento isotropico
La superficie di snervamento può crescere ma non cambia posizione
Incrudimento cinematico
La superficie di snervamento può solo traslare ma non
cambiare di forma
Condizione di consistenza
F  σ, ε pl   0
La superficie di snervamento segue l’evoluzione dello stato tensionale in modo che la disequazione
sia sempre rispettata
Un cambiamento dello stato tensionale si sviluppa elasticamente (scarico elastico) se
Si ha invece ulteriore plasticizzazione se si realizza una fase di carico
ulteriore con incremento della deformazione plastica
Materiali incrudenti
La superficie cresce in estensione dal
primo snervamento fino alla superficie
di rottura (il cammino è irreversibile)
dF  σ, ε pl   0
dF  σ, ε pl   0
Principio di normalità
Esso asserisce che in condizioni di incipiente uscita dalla curva limite di snervamento, la
deformazione plastica fluisce secondo una direzione che risulta normale alla curva limite stessa
In termini di equazioni, si può scrivere che, per ciascuna delle 6 componenti indipendenti
dell’incremento di deformazione plastica, si ha la condizione di parallelismo tra l’incremento plastico
di deformazione e la normale alla superficie di snervamento
d  ijpl pl  
F
 ij
(2)
La costante  è per ora niente di più che un fattore di proporzionalità che andrà determinato.
Nella plasticità associativa, di cui qui si discute, si ha che F risulta essere proprio la superficie di
snervamento prima definita
Se si considera plasticità non associativa (valida per esempio per materiali porosi che risentono della
tensione media) , allora occorre sostituire a F una funzione che definisca più appropriatamente il
potenziale plastico
Per ottenere un legame costitutivo coerente, nel caso elasto-plastico, si
suddivide la deformazione in una somma di contributo elastico e plastico
Ricordando il principio di normalità ed il legame tensionideformazioni in campo elastico e plastico
d  ijtot  d  ijel  d  ijpl
dε  D1dσ  
F
σ
Dove D - legame elastico - vale, nel caso tridimensionale




dε  




d  xx 
1
-
d  yy 

d  zz  1 -


d  xy  E  0
0
d  yz 


d  xz 
0
-
1
-
0
0
0
-
0 
-
0
0
0 
1
0
0
0 

0 1 
0
0 
0
0 1 
0 

0
0
0 1  
0
0









d xx 
d yy 
d zz 
  D dσ
d xy 
d yz 

d xz 
(3)
Come detto, quando si realizzano le condizioni di flusso plastico, la superficie limite si incrementa
(incrudimento) e fa si che essa continui ad inglobare lo stato tensionale raggiunto.
Questo vuol dire che il suo differenziale totale (incremento assoluto), composto da 7 termini, rimane
sempre nullo
dF 
F
F
F
F
F
F
F
d xx 
d yy 
d z 
d xy 
d yz 
d zx 
d  0
 xx
 yy
 zz
 xy
 yz
 zx

Definendo ora con
A
1 F
d
 
(4)
(5)
Utilizzando il vettore a 6 componenti di , l’equazione scalare (4) assume una forma semplificata
 F 
  dσ  A  0
 σ 
T
(6)
Se ora si raggruppano le eqq. (3) e (6) si perviene ad un sistema composto di 7 eq. in 7 incognite:
F 
 1
D
d
σ

 

σ
dε  


 
T
 0   F  dσ  A 
 σ 




(7)
Vediamo ora di discutere il significato del termine A. Chiaramente, se non si ha incrudimento,
esso si annulla in quanto F rimane lo stesso al crescere di 
Il punto di partenza è la determinazione del parametro  che misura il lavoro
incrementale di hardening, per cui la sua crescita vale
d  σT dε pl
d   xx d xxpl   yy d yypl  ...   zx d zxpl
Ricordando la legge di flusso
d  ijpl  
F
 ij
(2)
e sostituendola in quest’ultima
d    σT
F
σ
Che ci consente di eliminare il fattore d presente nella equazione (5)
A
F T F
σ

σ
(8)
Von Mises presenta il notevole vantaggio di poter esprimere il gradiente di F in modo agevole
F σ  
1
2
 xx   yy    yy   zz    zz   xx   3 xy2  3 yz2  3 zx2   y    0
2
2
2
Con semplici passaggi si scrivono le 6 derivate
3s
F
 x ;
 xx 2 eq
3s y
F

;
 yy 2 eq
3s
F
 z ;
 zz 2 eq
F
 xy

3 xy
 eq
;
F
 yz

3 yz
 eq
;
F
 zx

3 zx
 eq
;
Se si dispone di una semplice prova di trazione (monodimensionale), si ha a
disposizione una curva del tipo m - m , spostandosi dalla condizione di
incipiente snervamento, il lavoro incrementale di deformazione plastica è:
d   y d  m
Si esprime - in questo caso monodimensionale - il valore della prima derivata scalare presente
nella eq. (8) avendo bene in mente che il differenziale totale (4) risulta nullo
F
F
d s 
d  0
 s

F d y




d
=1
d y
Avendo definito
H
d m
1 d y

 y d m
H
y
H non è altro che la pendenza istantanea
della curva di incrudimento monotona.
F T F
Se ora si sostituisce nella (8) ricordando anche che nel caso monodimensionale la
A
σ
seconda derivata ivi presente vale semplicemente 1, si perviene ad una definizione di

σ
A H
Si può ora tornare al sistema (7)
cercando di darne una soluzione il più
possibile generale. In particolare
occorre approntare una opportuna strategia risolutiva che
rimanga valida anche quando A = 0, ossia il materiale
presenti un comportamento elasto-plastico perfetto
Lo scopo sarà quello di fare scomparire nel sistema (7) il termine λ.
 F 

 D
 σ 
T
Si comincia col premoltiplicare il primo set di equazioni (7) per il termine
F 

dε   D1dσ 


σ


F
 F 
 F 
 F 
1
D
d
ε

D
D
d
σ

D







σ
 σ 
 σ 
 σ 
T
T
T
Semplificando, e mettendo in evidenza il primo termine a destra dell'uguale, si ottiene il seguente
F
 F 
 F 
 F 
d
σ

D
d
ε

D







σ
 σ 
 σ 
 σ 
T
T
T
 F 

 dσ  A  0 (6)
 σ 
T
termine che può essere poi sostituito nel II set di equazioni (7) - che è poi
una semplice eq. Scalare - si elimina così il dσ
T
 F T F

 F 
 A   0

 D dε  
 D

σ

σ

σ





Quest’ultima permette di eliminare il fattore moltiplicativo
 F 

 D dε
 σ 

 F T F

D

A




σ

σ




T
(9)
F 

dε   D1dσ 


σ


Che viene infine eliminato nella prima delle (7)
 F 

 D dε

F
 σ 
dε  D1dσ 
σ  F T F

D

A




σ

σ




T
(10)
Ora si scrive la precedente equazione in termini espliciti, indicando cioè la variazione dello
stato tensionale per effetto di un incremento di deformazione totale (si premoltiplica per D)
F  F 
D

 D
σ  σ 
T
dσ  Ddε 
 F 

F
D

A




σ

σ




T
dε
(11)
In pratica si è trovato un legame incrementale tra il tensore di deformazione e quello della tensione
che si scrive noto che siano la matrice D del materiale elastico, l’ipotesi di rottura attraverso la
definizione di F e quindi delle sue derivate, la pendenza incrementale di incrudimento plastico (A).
F  F 
D

 D
σ  σ 
T
dσ  D*dε
D*  D 
 F T F

 A

 D

σ

σ




Questo modo di procedere fin qui descritto ha lo svantaggio di considerare una D* indipendente
dallo stato di tensione che di fatto fuoriesce istantaneamente dalla curva di snervamento
Se gli incrementi di deformazione sono sufficientemente piccoli l’errore che si commette non
è grande, tuttavia se così non è l’errore accumulato può diventare intollerabile.
In questo caso si può far ricorso all’algoritmo del return mapping, proposto nel 1964 da
Maenchen e Sacks. La tecnica prevede uno scaling della tensione in modo da permanere
sempre sulla superficie di incrudimento
Per il momento il sistema non viene descritto, si ritiene utile solo accennare al fatto che la
risoluzione comporta la ricerca di zeri della funzione attraverso l’algoritmo di Newton-Raphson.
Qualora la plasticità non fosse asssociativa, ugualmente la ricerca del punto finale sulla superficie
di snervamento va risolta in forma numerica
Esempio su deformazione 3D
 275.04 59.01 -202.86 
σ   59.01 260.36 -27.52 
-202.86 -27.52 -65.40 
Si ipotizza la presenza di un determinato stato di tensione e di
deformazione, giacenti sulla superficie limite di snervamento:
1  400 MPa
 2  230 MPa
 3  160 MPa
La quale presenta, come si può risolvere, tre tensioni principali pari a:
Secondo i criterio di Von Mises, essendo la tensione equivalente sulla curva di snervamento, si ha
una tensione di snervamento
 y  4002  2302  1602   400  230   230 160  160  400  497.29
Si calcola il tensore di
deformazione elastico, ipotizzando
di essere in regime elastico e
quindi di non aver ancora compiuto
lavoro plastico (=0):
 xx 
1
 
-
yy
 

 zz  1 -
 


E
xy
 
0
 yz 
0
 

 xz 
0
-
-
0
0
1
-
0
0
-
1
0
0
0
0
1 
0
0
0
0
1 
0
0
0
0
0 
0 
0 

0 
0 

1  
 xx 
 
 yy 
 zz 
 
  xy 
  yz 
 
  xz 
Ponendo per il materiale le seguenti caratteristiche:
 xx 
1
 
-
yy
 

 zz  1 -
 

 xy  E  0
 yz 
0
 

 xz 
0
E= 2.06e11 Pa,
H= 1/1000*E
-
-
0
0
1
-
0
0
-
1
0
0
0
0
1 
0
0
0
0
1 
0
0
0
0
0 
0 
0 

0 
0 

1  
=0.3,
sn=500 Mpa
 275.04   1.0512 
 260.36   0.9586 

 

 -65.40  -1.0972  3


 10
59.01
0.3724

 

 -27.52  -0.1737 

 

-202.86
-1
.2802

 

Da un calcolo complessivo, a partire da questo stato, si ha un incremento di deformazione totale
(di primo tentativo) ad esempio di semplice dilatazione unidirezionale in x , pari a 0.001:
ε new  ε old
  1.0512  1.0000 
 2.0512 





 0.9586 
  0.9586  0.0000


 -1.0972  0.0000 3 -1.0972  3
 dε   

 10  
 10
  0.3724  0.0000
 0.3724 
 -0.1737  0.0000
-0.1737 

 



 -1.2802  0.0000
-1.2802 
La prima verifica da fare è che l’incremento di deformazione totale faccia sforare la sollecitazione
equivalente oltre il limite di snervamento attuale:
 xx 
 
 yy 
 zz 
E
  
1   1  2  
 xy 
  yz 
 
  xz 
1-




 0
 0

 0

1-



1-
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1  2  
 eq  573.31 MPa  497.29 MPa
2
1  2  
0
2
0
1  2  
  2.0512 
 552.39 


 379.21 
  0.9586 


 -1.0972  3  53, 44 

 10  

  0.3724 
 59.01 
 -0.1737 
 27.52 




2  -1.2802 
202.86 
La sollecitazione esce dalla zona elastica
Con il che si evince che si è entrati in campo plastico e bisogna utilizzare la equazione (11) per il
calcolo del tensore delle tensioni.
Per poter applicare la (11) occorre calcolare le derivate del gradiente di F rispetto alle tensioni –
nell’ultimo punto noto in elasticità:
 m   x   y + z  3=156.67 MPa
sx   x   m =118.37 MPa
sxy   xy = 59.01 MPa
s y   y   m =103.70 MPa
s yz   yz =  27.52 MPa
sz   z   m = -222.07 MPa
sxz   xz = -202.86 MPa
F
 xx
F
 xy


3 118.37
 0.3571;
2  497.29
3  59.01
 0.3560;
497.29
F
 yy
F
 yz

 F 

   0.3571
 σ 

3 103.70
 0.3128;
2  497.29
F
 zz
3   27.52 
 0.1660;
497.29
F
 zx


T
0.3128
-0.6698
3   222.07 
 0.6698;
2  497.29
0.3560
3   202.86 
 1.2238;
497.29
0.1660 1.2238
Calcolando ora la (12) si ottiene
T
D*  D 
F  F 
D

 D
σ  σ 
 F T F

D

A



σ
 σ 

 2.6863
 1.1358

 1.4816
 1105 
-0.1559
-0.2739

 0.0727
1.1124
1.3513
-0.0865
0.0404
2.7065
1.3311
-0.0758
0.0354
1.3063
2.4676
0.1624
-0.0757
-0.0627
0.3485
1.4983
0.0402
-0.1101
0.6124
-0.3256
1.5659
0.0292
-0.1625
0.0864
0.1518
Per cui, osservando che
dσT   D*dε    268.63 111.24 135.13
T
0.2975 
0.2606 
-0.5582 

0.2966 
-0.1383 

0.5649 
dσ  D*dε
8.66
4.04
29.75  MPa
Si determina anche il nuovo stato di tensione
σ  σ  dσ   543.67
371.61
69.73
173.11
23.11
50.36
Con una nuova tensione di snervamento
T
MPa
 y  521.38 MPa
Evidentemente più bassa di quella estrapolata al primo tentativo elastico (573.31 MPa)
 F 

 D dε

σ


4


51.53

10
 F T F

 A

 D

σ

σ



T
Il parametro λ può essere ora calcolato dalla (9):
E il lavoro incrementale di hardening (per unità di volume) assume il valore
d    σT
F
=
σ
51.53 104   543.67
 0.3571
0.3128
371.61
-0.6698
69.73
0.3560
50.36
23.11
0.1660 1.2238
173.11 
'

0.0763 Nmm
Il punto debole del calcolo precedente è la determinazione del gradiente di tensione, preso nello stato
precedente alla deformazione aggiuntiva
Qualora tale gradiente dovesse modificarsi in modo significativo per effetto della deformazione
imposta dallo step, occorrerà ridurre gli intervalli di crescita di deformazione, in modo da inseguire
l’evoluzione dell’incrudimento restando sempre sulla superficie (aggiornata) di snervamento stessa
Questo modo di procedere risponde al nome di Return Mapping ed esistono svariati modi di
procedere in funzione anche del metodo utilizzato per calcolare la tensione equivalente
Nel calcolo agli elementi finiti, il modo di precedere si inserisce negli step di calcolo non lineare,
come ad esempio nello svolgimento del metodo di Newton Raphson.
Tale metodo prevede lo svolgimento di iterazioni, e quindi l’assunzione di un campo di spostamenti
di tentativo, che viene via via affinato finché non si raggiunge un equilibrio soddisfacente tra le
forze esterne applicate e le forze interne che si sviluppano
Il problema del calcolo elasto-plastico del materiale nasce proprio per la valutazione delle forze
interne, la cui definizione richiede la soluzione del legame non lineare tra deformazioni e tensioni
Pertanto, ad ogni iterazione si considera un sottoincremento dello spostamento
In modo da ottenere
u  i ui
ε  i εi e quindi ricercare le conseguenti variazione di tensione
Questa operazione è ripetuta per ogni elemento, in corrispondenza ad ognuno dei suoi punti
di Gauss, utilizzati per l’integrazione numerica
In pratica, la tensione, dipendente dal valore assunto al passo precedente, si risolverà da una
sommatoria che contiene integrali del tipo
σ n 1  σ n  σ n 
 εi * 
σ n   i   Di dε 


0

Il modo esplicito più semplice di affrontare questo problema è di approssimare l’integrale
considerando un valore costante nell’arco di integrazione. Questo metodo è molto rapido, ma
decisamente poco preciso a meno che non si suddivida in intervalli molto piccoli e di dimensione
difficilmente prevedibile
In alternativa, si può determinare ciascun integrale con un approccio alla Runge-Kutta del II
*
ordine, che conduce ad una doppia stima della matrice tangente Di
Si impone una deformazione pari alla metà di quella effettiva e si
calcola la tensione relativa
Con questo incremento di tensione si ridetermina la matrice tangente
che viene utilizzata per il calcolo dell’intero stato tensionale
Questo metodo risolutivo consente anche di avere una stima
dell’errore mediante l’espressione
σ 1 2 
1 *
D0 ε
2
σ 1  D*01 2 ε
err  σ 1  2σ 1 2
Il metodo può comportare il continuo scostamento del tensore della tensione dalla curva di Yielding
In alternativa è stato sviluppato il metodo del Return-Mapping (1964), del quale si può dare una
semplice interpretazione geometrica dalla figura sottostante
In pratica si impone di riportare lo stato di tensione sulla curva di snervamento, mediante tratti di
ritorno tutti ortogonali e di livelli di incrudimento decrescente. L’algoritmo impone che lo stato di
tensionale finale corrisponda ad una tensione equivalente pari a quella di snervamento attualizzata
I dettagli operativi dipendono dal modello costitutivo utilizzato per la valutazione della plasticità
Dal punto di vista del codice di calcolo agli elementi finiti, si possono comunque prevedere i
seguenti passaggi
1) Assunzione della deformazione totale:
procedimento non lineare di calcolo
εn
allo step n secondo un’iterazione del
2) Calcolo della deformazione di trial eliminando la parte già
plastica al passo precedente
plast
εtrn  ε n  ε n
1
3)
Determinazione della tensione di trial che si avrebbe se il
materiale reagisse linearmente
plast
σtrn  D  ε n  ε n
1 
4)
Calcolo della tensione equivalente per valutare se si rimane in regime elastico o se
si rientra in un tratto di plasticità
5)
Risoluzione, mediante la formulazione esplicita (oppure il return mapping) del
moltiplicatore plastico λn e quindi della parte plastica dell’incremento di deformazione
ε nplast  n
F
σ
6) Determinazione della componente elastica e plastica della deformazione totale
εelast
 εtrn  ε nplast
n
7)
plast
ε nplast  ε nplast
1  ε n
Calcolo dello stato tensionale presente (dovuto solo alle deformazioni elastiche)
σ n  Dεelast
n
8)
Aggiornamento dell’incremento del lavoro plastico di incrudimento e dell’incremento plastico
equivalente della deformazione (per utilizzare la curva monotona)
d n  n σTn
F
σ
 n   n1  d n
 eqpl 
2 plT pl
ε ε
3