Liceo Scientifico Statale “G. Peano” - Cuneo
PROGRAMMA DI MATEMATICA
Prof.ssa Fabrizia De Bernardi
CLASSI VC - VH
anno scolastico 2011/12
Introduzione all’analisi matematica
Problema della rettificazione della circonferenza e della quadratura del cerchio.
Proprietà dell’insieme dei numeri reali dal punto di vista algebrico e topologico. Definizione di intervallo e
intorno. Successioni numeriche, estremo superiore, inferiore, massimo e minimo di una successione
numerica. Punti di accumulazione.
Funzioni reali di una variabile reale
Concetto di funzione, dominio, codominio e grafico. Funzioni iniettive, suriettive, biiettive. Funzioni pari e
dispari. Ripasso delle principali funzioni elementari e loro grafici: funzione lineare, quadratica, omografica,
funzioni goniometriche, funzione esponenziale, logaritmo, valore assoluto. Funzioni composte.
Campo di esistenza di una funzione. Funzioni monotòne e invertibili.
Limiti di una funzione reale di variabile reale.
Le quattro definizioni di limite. Verifica di limiti tramite la definizione. Teoremi fondamentali sui limiti (con
dimostrazione). Infinitesimi e infiniti. Infinitesimi equivalenti. Operazioni sui limiti.
Definizione di funzione continua. Continuità delle funzioni elementari e composte.
Proprietà delle funzioni continue in un intervallo chiuso e limitato; teorema di Weierstrass, teorema
dell’esistenza degli zeri, risoluzione grafica di equazioni e disequazioni, teorema di Darboux-Bolzano.
Teorema di monotonia.
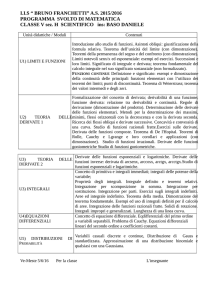
Limiti fondamentali:
lim sen x
=1
x→0 x
,
x
lim
1
1 + = e
x → ∞
x
e altri limiti da questi derivanti (dimostrazioni).
Forme indeterminate di limite. Calcolo di limiti. Punti di discontinuità.
Derivate delle funzioni reali di variabile reale.
Definizione analitica e significato geometrico. Relazione tra continuità e derivabilità. Calcolo di derivate
tramite la definizione. Derivate delle funzioni elementari, derivate della somma, del prodotto e del rapporto
di funzioni. Derivata della funzione composta e della funzione inversa. Funzioni iperboliche: grafici e
derivate. Derivata logaritmica.
Applicazioni delle derivate alla geometria analitica e alla fisica, in particolare alla cinematica (moto rettilineo
e curvilineo).
Teoremi fondamentali del calcolo differenziale: Rolle, Lagrange (e conseguenze), Cauchy (con
dimostrazione). Regola di De L’Hôpital. Formula di Taylor e di Mc Laurin.
Differenziale: definizione e significato geometrico.
Definizione di massimo e minimo relativo e assoluto. Massimi e minimi delle funzioni derivabili. Criteri e
teoremi (con dimostrazione). Problemi di massimo e minimo in aritmetica, geometria, trigonometria.
Derivata seconda, concavità e convessità, punti di flesso (teoremi con dimostrazione). Asintoti obliqui.
Cenni alla discussione grafica di una equazione.
Integrali
Integrali indefiniti. Definizione. Continuità e integrabilità. Integrali immediati. Metodi di integrazione
(scomposizione, sostituzione, per parti). Integrazione di funzioni razionali fratte. Altri integrali particolari.
Integrale definito. Problema delle aree. Definizione. Teorema della media, teorema fondamentale del calcolo
integrale (con dimostrazione). Calcolo di integrali definiti e applicazioni: aree, volumi di solidi di rotazione,
alcuni integrali di volume di altro tipo. Applicazioni alla fisica. Integrali impropri. Cenni alle eq.
differenziali.
Calcolo combinatorio
Disposizioni, combinazioni, permutazioni, coefficienti binomiali e binomio di Newton.
Libro di testo:
Dodero-Baroncini-Manfredi, Elementi di Matematica, Vol.3, Ed.Ghisetti e Corvi.
Cuneo, 12 settembre 2011
L’insegnante _______________________________
Liceo Scientifico Statale “G. Peano” - Cuneo
PROGRAMMA DI FISICA
CLASSI VC - VH
anno scolastico 2011/12
OTTICA ONDULATORIA
Diffrazione attraverso una fenditura. Interferenza: esperimento di Young. Polarizzazione della luce.
ELETTROSTATICA
Esperimenti di elettrostatica. Legge di Coulomb. Concetto di campo e campo elettrostatico. Campo di una
carica puntiforme e di un dipolo elettrico. Flusso del campo elettrico. Teorema di Gauss e sue applicazioni.
Energia potenziale elettrostatica e potenziale elettrostatico. Moto di una carica in un campo elettrico
uniforme. Esperienza di Millikan (Alonso-Finn). Capacità di un conduttore. Condensatore. Condensatori in
serie e in parallelo. Circuitazione del campo elettrostatico. Polarizzazione del dielettrico (Quaglino).
CONDUZIONE ELETTRICA NEI SOLIDI
Definizione di intensità di corrente elettrica. Leggi di Ohm.(Quaglino) Resistenze in serie e in parallelo.
Forza elettromotrice: legge di Ohm generalizzata. Lavoro e potenza della corrente. Legge di Joule. Principi
di Kirchhoff. Circuito RC.
CONDUZIONE ELETTRICA NEI LIQUIDI
Leggi di Volta. Elettrolisi. Leggi di Faraday. Cenni ai generatori di f.e.m.
CONDUZIONE ELETTRICA NEI GAS
Scarica nei gas. Ionizzazione a valanga. Arco voltaico. Conduzione nel vuoto: tubi catodici.
Effetto termoelettronico e termoelettrico.
ELETTROMAGNETISMO
Il campo magnetico: forza di Lorentz e definizione del vettore induzione magnetica. Moto di una carica in un
campo magnetico. Interazione corrente-magnete: esperimento di Oersted. Interazione tra correnti: legge di
Ampère, legge di Biot-Savart. Teorema della circuitazione di Ampère. Flusso del campo magnetico e
teorema relativo. Momento agente su una spira immersa in un campo magnetico. Esperimento di Thomson
per la misura di e/m.
Sostanze diamagnetiche, paramagnetiche e ferromagnetiche. I vettori H ed M. Ciclo di isteresi.
Induzione elettromagnetica. Esperienze di Faraday. Legge di Faraday-Lenz. Autoinduzione e induttanza.
Circuito RL. Circuito LC. Produzione della corrente alternata. Circuito RCL: trattazione con il metodo dei
fasori. Campo elettrico indotto. Corrente di spostamento. Equazioni di Maxwell. Onde elettromagnetiche e
loro proprietà: trasporto di energia e quantità di moto, polarizzazione della luce. Calcolo della velocità della
luce nel vuoto (Halliday-Resnick). Il vettore di Poynting, la pressione di radiazione. La polarizzazione della
luce (Halliday-Resnick).
Importanza e conseguenze delle equazioni di Maxwell. Nascita della relatività ristretta, cenni.
ORIGINI DELLA FISICA QUANTISTICA (Halliday-Resnick)
Radiazione del corpo nero. Legge di Planck e quantizzazione dell’energia. Effetto fotoelettrico. Teoria dei
fotoni di Einstein. Effetto Compton.
De Broglie e il dualismo onda-corpuscolo della materia. Equazione di Schrödinger e significato della
funzione d’onda. Principio di complementarità di Bohr. Principio di indeterminazione di Heisenberg: un
esperimento ideale di diffrazione degli elettroni come verifica dello stesso.
Libro di testo
Ugo Amaldi, La fisica di Amaldi, Idee ed esperimenti, Vol.3, Ed. Zanichelli
Cuneo, 12 settembre 2011
L’insegnante ____________________________