Storia della logica dall’antichità
a Boole
S.I.S.S.I.S.
I anno
Autore:
Antonio Monteleone
Indirizzo II Fisico-Matematico-Informatico
Classe 49A
Prof. T.Marino
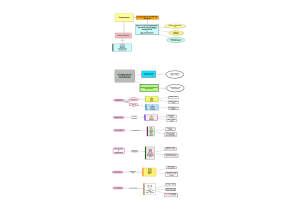
Pensatori
contemporanei
o
antecedenti a Platone
(VI – V secolo a.C.)
E’ probabile che si siano posti problemi inerenti la natura della
dimostrazione, sui nessi che legano premesse e conclusioni e sulle
condizioni che determinano la validità di un argomento. Le loro opere sono
andate perdute.
Platone (V – IV secolo
a.C.)
Nei Dialoghi si ritrovano alcune discussioni su argomenti di carattere
logico.
Aristotele
a.C.)
(IV
secolo Si ha una riflessione sistematica sulla logica. L’invenzione logica più
importante è la teoria del sillogismo. Il suo lavoro è incentrato sulla logica
dei termini.
Scuola
Megarico- Viene sviluppato il pensiero logico di Aristotele e formulata una logica
Stoica (IV – III secolo delle proposizioni. Si distingue tra argomenti e proposizioni al fine di
mettere in evidenza la differenza tra validità e verità. C’è più
a.C.)
consapevolezza rispetto ad Aristotele di costruire un vero e proprio sistema
assiomatico.
Medioevo (XI – XIV Vengono riprese e sviluppate le tradizioni logiche aristoteliche e megaricostoiche, con la preoccupazione di chiarire i punti oscuri della logica antica.
secolo)
Vengono prodotte due trattazioni originali relative rispettivamente ai
termini (teoria della suppositivo) e alle proposizioni (teoria delle
consequentiae)
Leibniz (XVII secolo)
In seguito ad un decisivo sviluppo del calcolo algebrico, propone di
stabilire uno stretto rapporto tra logica e matematica. E’ il primo a coniare
il termine logica matematica. Costruisce la Characteristica universalis,
ovvero un linguaggio artificiale nel quale si proponeva di esprimere i
concetti, i principi e le dimostrazioni del calcolo. Non riesce a portare a
termine il suo obiettivo, però formula un calcolo delle classi in grado di
adattarsi anche alle proposizioni.
Boole (XIX secolo)
Raggiunge i risultati auspicati da Leibniz. Influenzato dallo sviluppo del
calcolo algebrico inglese (Hamilton), studia le proposizioni logiche
principali (congiunzione e disgiunzione) riuscendo a costruire un algebra
suscettibile di una doppia interpretazione: puramente logica (le variabili
sono simboli per classi) o numerica (0 e 1), rendendo così conto sia della
logica per classi che della logica delle proposizioni. La logica con Boole
diventa matematica, non solo perché fa uso di un apparato simbolico e
metodi tipici della matematica, ma anche perché si rivolge all’analisi di
questioni e problemi interni alla matematica.
2
Storia della logica dall’antichità a Boole
Fino alla seconda metà del secolo XIX la logica, nell’ambito della cultura occidentale, ha
fatto parte esclusivamente del corpo delle discipline filosofiche. Nonostante ciò all’interno di tali
discipline, la logica ha occupato un posto peculiare, infatti si può dire che sia stata l’unica
tramandata per mezzo di trattati sviluppati secondo tecniche e procedimenti considerati standard,
al punto che anche quando sorgeva una disputa tra eminenti logici, questi si ritrovavano
d’accordo su gran parte dei contenuti caratterizzanti la disciplina. Sotto questo aspetto si può
dire che la logica abbia avuto più affinità con la geometria piuttosto che con la filosofia e tale
caratteristica, si è ulteriormente accentuata dopo il XIX secolo, grazie ad un rapporto fittissimo
con la matematica, anche se non è mai andato perduto il legame con le sue origini filosofiche.
E’ probabile che pensatori antecedenti o contemporanei a Platone si siano posti problemi sulla
natura della dimostrazione, sul tipo di nesso che lega premesse e conclusioni in un ragionamento
corretto e sulle condizioni che determinano la validità di un argo mento, ma tali opere sono
andate perdute, solo nei Dialoghi di Platone (V-IV sec. a.C.) si è potuto riscontrare una
discussione su argomenti di carattere logico.
E’ però con Aristotele che si ebbe una riflessione sistematica circa la logica, intesa come
disciplina autonoma. Il pensiero logico di Aristotele è stato sviluppato in un gruppo di opere che
presero il nome di Organon e comprendente sei trattati:
1. Categorie;
2. De Interpretazione;
3. Analitici primi;
4. Analitici secondi;
5. Topici;
6. Elenchi sofistici.
Le Categorie contengono una discussione concernente i concetti più generali ai quali vengono
ricondotti tutti gli altri; il De Interpretazione presenta un’analisi delle varie parti del discorso e
dei rapporti tra segni linguistici, concetti e significati; gli Analitici primi e secondi contengono
gran parte della teoria del sillogismo; i Topici comprendono un’analisi dei procedimenti
argomentativi mossi da premesse generalmente accettate, ma non proprie del discorso
scientifico; gli Elenchi sofistici prendono in esame i paradossi, dandone criteri generali per
risolverli.
L’invenzione logica più originale di Aristotele fu la teoria del sillogismo, la quale, in seguito
alla ripresa della logica nel Medioevo, assunse una sorta di forma standard che rimase tale fino
al XIX secolo e che venne chiamata concezione tradizionale del sillogismo. Si dà una
esposizione sintetica di tale teoria al fine di metterne in risalto le differenze con quella originaria
di Aristotele.
Consideriamo un esempio concreto di sillogismo:
3
1. Tutti gli uomini sono mortali.
2. Tutti i Greci sono uomini.
Dunque:
3. Tutti i Greci sono mortali.
Le proposizioni 1 e 2 sono chiamate premesse, la terza è chiamata conclusione. I termini che
compaiono nelle tre proposizioni sono “uomini”, “Greci” e “mortali”, tra questi “uomini”
compare in entrambe le premesse e non nella conclusine, per cui lo chiamiamo termine medio.
Sostituiamo “uomini” con la lettera M, “Greci” con S, “mortali” con P e l’espressione “dunque”
con un tratto orizzontale. Otteniamo così:
1. Tutti gli M sono P.
2. Tutti gli S sono M.
—————————
3. Tutti gli S sono P.
In tal modo si ottiene uno schema di sillogismo, nel quale al posto di S, M e P si possono
sostituire termini qualunque.
Combinando i termini S, M, P e tenendo conto che M deve comparire almeno una volta in
ciascuna premessa e che la conclusione deve essere della forma “S P”, si ottengono 4
configurazioni.
I
II
III
M
P
M
S
————
S
P
IV
M
P
P
M
P
M
S
M
S
M
M
S
————
————
————
S
P
S
P
S
P
Tab.1.1. Le figure del sillogismo.
Tali configurazioni vengono chiamate le figure del sillogismo. Le figure, comunque, non
danno alcuna informazione sulla forma che possono assumere le proposizioni che compongono
un sillogismo. Esistono infatti, altre forme oltre a quella già vista del tipo “Tutti gli A sono B” e
precisamente:
tab. 1.2
PROPOSIZIONI
FORMA DELLE PROPOSIZIONI
Universali Affermative (A)
“Tutti gli A sono B”
Particolari affermative ( I )
“Qualche A è B”
Universali negative
(E)
“Nessun A è B”
Particolari negative
(O)
“Qualche A non è B”
4
Le vocali maiuscole tra parentesi permetteranno di riferirci alle proposizioni citate con più
semplicità.
Ai tipi di proposizione presentati vengono aggiunte le proposizioni singolari, cioè quelle che
hanno per soggetto un nome proprio (es. Socrate è un uomo). Le 4 proposizioni della tab. 1.2.
possono essere distinte secondo la quantità e secondo la qualità.
UNIVERSALI
PARTICOLARI
Tab. 1.3
AFFERMATIVE
Tutti gli A sono B
Qualche A è B
NEGATIVE
Nessun A è B
Qualche A non è B
I rapporti, dal punto di vista logico, tra tali proposizioni possono essere messi in evidenza
facendo riferimento al cosiddetto “quadrato logico”, mostrato nella tab. 1.4.
A—————Contrarie—————E
Subalterne
Subalterne
I—————Subcontrarie————O
contraddittorietà
Tab. 1.4. Il quadrato logico delle proposizioni.
Le proposizioni di tipo A e E sono tra loro contrarie, cioè non possono essere entrambe vere,
ma possono essere entrambe false (es. “Tutti i mammiferi vivono sulla terraferma” e “Nessun
mammifero vive sulla terraferma”).
Le proposizioni I e O sono, rispettivamente, la subalterna di A e la subalterna di E, cioè se
l’universale è vera risulterà vera anche la particolare della stessa qualità, naturalmente non vale
il viceversa.
Le proposizioni O e A sono contraddittorie, cioè non possono essere entrambe vere o
entrambe false. Lo stesso vale per le proposizioni I e E.
Infine, le proposizioni I e O possono essere entrambe vere, ma non entrambe false (es.
“Qualche vertebrato è uomo” e “Qualche vertebrato non è uomo”).
Le proposizioni A, E, I, O, poiché si limitano a indicare se un certo soggetto ha o non ha un
detto predicato, sono chiamate categoriche. Poiché ciascuna proposizione che compone un
sillogismo può essere categorica, in ogni figura il numero delle combinazioni che si ottengono
considerando il numero delle proposizioni del sillogismo (3) e il numero delle forme (4) che
ciascuna proposizione può assumere, sarà uguale a 4 3, cioè a 64. Se chiamiamo modo la forma
5
che un sillogismo assume dopo averne specificato la quantità e la qualità delle premesse e della
conclusione, si ottiene che, poiché le figure sono 4, la totalità dei modi sarà 64×4=256. Dei 256
modi, non tutti rispettano le regole del sillogismo e solo 19 possono essere considerati validi.
Al fine di esporre tali regole, bisogna precisare una definizione. Un termine di una
proposizione categorica si dice che è preso universalmente o quando, essendo soggetto, gli è
applicata l’espressione “tutti” o l’espressione “nessuno”; oppure quando, essendo predicato, si fa
riferimento alla totalità degli individui compresi nella classe che esso designa (es. “Nessun A è
B”: sia il soggetto che il predicato sono presi universalmente; “Tutti gli A sono B”: solo il
soggetto è preso universalmente).
Regole sui termini
1 (a). Il termine medio deve essere preso universalmente in almeno una
premessa.
2 (a). Nessun termine può essere preso universalmente nella conclusione, senza
che sia stato preso universalmente in una delle premesse.
Regole sulle proposizioni
1 (b). Da premesse negative non segue alcuna conclusione.
2 (b). Se una premessa è negativa, la conclusione deve essere negativa; se una
premessa è particolare, la conclusione deve essere particolare.
Le regole del sillogismo sopra riportate tendono a garantire certi nessi di dipendenza tra i
termini e quindi tra le premesse e la conclusione, in modo che quest’ultima derivi in modo
naturale dalle premesse; è importante, però, sottolineare che la verità della conclusione deve
essere mantenuta distinta dalla validità di quello stesso sillogismo.
Individuati quindi, i modi validi, la tradizione sillogistica, sulla base di indicazioni fornite da
Aristotele, elaborò un meccanismo di riduzione di certi sillogismi ad altri allo scopo di
dimostrarne la validità. Tale meccanismo consisteva nel considerare nell’insieme dei 19 modi
validi, 4 come autoevidenti o perfetti, e mediante certe regole di trasformazione riuscire a
trasformare un dato sillogismo in uno autoevidente, dimostrandone così la validità. Le regole di
trasformazione principali sono: la conversione semplice e la conversione per limitazione.
La conversione semplice permette di passare da una proposizione p in forma soggettopredicato ad una proposizione p' avente per soggetto il predicato di p e per predicato il soggetto
di p (tale passaggio è possibile solo nel caso delle proposizioni I e E, infatti da “Qualche A è B”
è lecito inferire “Qualche B è A e da “Nessun A è B” è lecito inferire “Nessun B è A”).
La conversione per limitazione consente di passare da una proposizione p categorica di tipo A
ad una proposizione p' categorica di tipo I avente per soggetto il predicato di p e per predicato il
soggetto di p (es. da “Tutti gli uomini sono mammiferi” si può inferire “Qualche mammifero è
uomo”).
6
Altre regole necessarie per la riduzione sono lo scambio di premesse e in alcuni casi un
procedimento dimostrativo per assurdo che quando viene applicato porta ad una riduzione
indiretta.
Il modo di concepire il sillogismo sopra riportato, cioè di considerare tre proposizioni distinte
non è l’unico ammissibile, infatti le tre proposizioni che possiamo indicare con p, q, r possono
costituire un’unica proposizione nella forma “Se p e q, allora r”. In quest’ultimo caso p, q, r
non vengono considerate come proposizioni isolate a cui bisogna dare un assenso, bensì come
parti integranti di un’unica proposizione. Questa differenza era netta nel sillogismo tradizionale,
ma non per Aristotele, il quale passava da una forma all’altra senza alcuna attenzione. Aristotele
inoltre privilegiava un modulo espressivo che spesso portava a complicazioni riguardo all’ordine
delle premesse e nel suo sillogismo non erano ammessi i termini singolari, trattati invece nel
sillogismo tradizionale.
Non tutte le nostre argomentazioni quotidiane o i nostri ragionamenti in ambito scientifico,
pur mantenendo la loro correttezza, si rifanno all’uso sistematico di sillogismi. Fu la scuola
megarico-stoica a mettere in evidenza altri tipi di ragionamento, sviluppando una logica attenta,
più che ai rapporti tra termini ai rapporti tra proposizioni.
I principali esponenti di tale scuola furono: Euclide di Megara, Diodoro Crono; Filone di
Megara; Zenone di Cizio, fondatore della scuola stoica; Crisippo di Soli, grande logico che
sollevò la scuola stoica da una grave crisi. I megarico-stoici distinsero tra proposizioni
categoriche e proposizioni ipotetiche. Le categoriche erano del tipo A, I, E, O e potevano
ulteriormente essere analizzate nei termini che le componevano e non in altre proposizioni. Le
ipotetiche invece, erano le proposizioni che si ottenevano unendo tra loro due o più categoriche
e quindi potevano essere scomposte in ulteriori proposizioni. Le ipotetiche fondamentali
venivano classificate in base al modo in cui erano unite le categoriche che le componevano e
cioè se p e q erano due proposizioni categoriche:
• “p e q” era chiamata ipotetica congiuntiva.
• “p o q” era chiamata ipotetica disgiuntiva.
• “se p, allora q” era chiamata ipotetica condizionale.
I medioevali in seguito introdussero altre ipotetiche come la causale:“ q, poiché p”; ma quelle
prima menzionate erano le più importanti, in quanto si poteva risalire alla loro falsità o verità
tenendo conto esclusivamente della verità o falsità delle proposizioni componenti.
I megarico-stoici furono i primi a dedicarsi allo studio dei connettivi logici. Essi proposero
che una proposizione nella forma “p e q” fosse vera solamente nel caso in cui p e q fossero
entrambe vere, falsa altrimenti; considerarono una proposizione “p o q” vera soltanto se almeno
una tra p e q fosse stata vera, falsa altrimenti. Questo uso del connettivo “o” è chiamato
inclusivo, ma gli esponenti di tale scuola formularono anche l’uso esclusivo
di “o”,
considerando “p o q” vera soltanto se una tra p e q fosse stata vera. Per quanto riguarda la
proposizione del tipo “se p, allora q” ci furono diverse interpretazioni. Filone di Megara propose
7
che tale proposizione fosse falsa esclusivamente nel caso di p vera e q falsa, cioè la definizione
di quella che in seguito sarà chiamata l’implicazione materiale. Diodoro Crono diede
un’interpretazione legata al tempo, infatti propose che “se p, allora q” fosse falsa esclusivamente
nel caso in cui nel tempo in cui l’antecedente era vero, il conseguente era falso. Infine Crisippo
propose che tale proposizione fosse falsa solamente nel caso in cui l’antecedente p era
compatibile con la negazione del conseguente q, dando così la prima caratterizzazione
dell’implicazione stretta.
I megarico-stoici studiarono a fondo anche il connettivo non, distinguendo tra quando esso
veniva usato davanti ad un termine e quando veniva usato davanti ad una proposizione. In
quest’ultimo caso ritennero che la proposizione non p fosse vera se p era falsa e falsa se p era
vera e stabilirono che non non p equivaleva a p. Essi distinsero tra argomento e proposizione.
Definirono un argomento come un sistema di proposizioni composto da premesse e da una
conclusione e su tale distinzione basarono la differenza tra validità e verità. Un argomento
valido era un argomento dove la negazione della conclusione era incompatibile con la
congiunzione delle premesse; un argomento valido vero era un argomento valido con premesse
vere; un argomento falso era un argomento che o non era valido o che aveva almeno una
premessa falsa; un argomento valido falso era un argomento valido per la sua forma, ma falso in
relazione alla falsità di una o più premesse.
Come aveva fatto Aristotele per la sillogistica, anche i megarico-stoici, tra l’insieme di tutti i
possibili argomenti, ne isolarono alcuni che considerarono indimostrabili e cercarono di provare
la validità degli altri, riducendoli mediante uso di regole ai primi. Tuttavia esistono delle
differenze, i megarico-stoici rispetto ad Aristotele erano più consapevoli di costruire un vero e
proprio sistema assiomatico, la loro è una logica delle proposizioni, più che una logica dei
termini, ciò non vuol dire che Aristotele non avesse conosciuto o fatto uso della logica delle
proposizioni, ma che egli non produsse alcuna teoria esplicita di questo tipo, per cui tale
invenzione rimase il contributo maggiore fornito alla logica dalla tradizione megarico-stoica.
Nel passaggio dall’antichità al Medioevo, come per tutte le altre discipline filosofiche e
scientifiche, la logica subì un periodo di oscurità. Una certa ripresa si ebbe a partire dal XI
secolo, e da lì una notevole accelerazione che portò allo straordinario sviluppo del XIII e XIV
secolo. Gli autori più importanti di questo periodo furono: Pietro Ispano (circa 1230), autore
delle Summulae logicales molto diffuse grazie all’invenzione della stampa; Boezio di Dacia
(seconda metà del XIII secolo), noto per aver collegato temi di riflessione logica a tematiche di
filosofia del linguaggio; Guglielmo di Ockham (XIV secolo), autore di una Summa logicae che
ebbe grande influenza nel formare la mentalità scientifica dei secoli successivi; Walter Burleigh,
contemporaneo e avverso a Ockham; Giovanni Buridano (seconda metà del XIV secolo); Paolo
Veneto (morto nel 1429), autore di una Logica che racchiudeva tutto il sapere logico
medioevale.
I logici medioevali distinguono tra due classi di termini: quelli che hanno un significato di per
sé (es. “tavolo”, “mare”, etc.) e quelli che hanno significato solo quando sono applicati ai primi
8
(es. “non”, “tutti”, “qualche”, “se…allora”, etc.). I primi vennero chiamati termini
categorematici e i secondi termini sincategorematici. Questa distinzione veniva usata dai
medioevali per separare l’aspetto materiale da quello formale in qualsiasi argomento o
proposizione. Infatti la forma logica era determinata dai termini sincategorematici e l’aspetto
materiale da quelli categorematici. Sulla base di questa distinzione i medioevali differenziavano
le proposizioni vere per la forma, cioè indipendentemente dal significato dei termini
categorematici in esse presenti, e quelle vere per la materia, per la cui falsità o verità era
necessario conoscere il significato dei termini categorematici. Rispetto alla tradizione antica, i
medioevali produssero due trattazioni originali relative rispettivamente ai termini e alle
proposizioni: la teoria della suppositio, dove erano studiate le condizioni di verità delle
proposizioni categoriche A, E, I, O e di quelle singolari, e la teoria delle consequentiae che
trattava gli argomenti e le proposizioni logicamente valide.
Nel XVII secolo compare per la prima volta l’idea di stabilire uno stretto rapporto tra la
logica e la matematica, fino ad allora considerate due discipline che studiavano ambiti della
conoscenza aventi fini e oggetti diversi. Ciò fu dovuto ad un decisivo sviluppo della matematica,
in particolare del calcolo algebrico introdotto da François Viète (1540-1603) e all’opera di
Gottfried Wilhelm Leibniz (1646-1716). Leibniz fu il primo ad introdurre il termine “logica
matematica” e a concepire un programma di matematizzazione della logica consistente nella
costruzione di un linguaggio artificiale nel quale esprimere i concetti, i principi e le
dimostrazioni del calcolo. Costruito tale linguaggio, chiamato characteristica universalis, si
sarebbero dovuti individuare i concetti fondamentali da cui tutti gli altri dipendono, adattare a
tali concetti dei segni ed esprimere le regole per passare da stringhe di segni alle corrispondenti
proposizioni. La logica in tal modo, sarebbe stata costituita dall’insieme dei principi e delle
regole che avrebbero dovuto garantire il corretto svolgersi delle dimostrazioni, e la sua
matematizzazione sarebbe consistita nell’avere le caratteristiche di un calcolo algebrico.
Leibniz si era prefisso un compito arduo che non sarà capace di portare a termine, comunque
riuscirà a costruire un vero e proprio calcolo delle classi, in grado di adattarsi anche alle
proposizioni. Con Leibniz, quindi, si ha l’unificazione dei due tipi di
calcolo che avevano
caratterizzato la logica fino ad allora.
Nonostante la ricchezza e l’originalità degli scritti leibniziani, alla morte dell’autore questi
vennero dimenticati. Altri studiosi, dopo Leibniz, si proposero di assimilare la logica ad un
calcolo cercando di far corrispondere la congiunzione e la disgiunzione logica alle operazioni di
somma e prodotto, considerando la copula come una uguaglianza e facendo riferimento
all’algebra, incappando spesso, però, in errori per aver inteso l’analogia con la matematica in
modo eccessivamente meccanico. A raggiungere i risultati auspicati da Leibniz sarà George
Boole (1815-1864), il quale poté far riferimento sullo sviluppo dell’algebra inglese
dell’Ottocento e sui risultati ottenuti da W. Rowan Hamilton (1805-1865), il quale aveva
dimostrato la possibilità di un’algebra in cui non valeva la proprietà commutativa del prodotto.
9
Boole s’interessò allo studio delle proposizioni logiche principali (congiunzione e
disgiunzione), influenzato dalla concezione (inglese) dell’algebra come una sorta di gioco, in cui
partendo da un insieme di simboli e definendo alcune operazioni si arrivava per via puramente
combinatoria ad un altro insieme di simboli coerente con quello di partenza. Boole si accorse
che le proprietà rilevate dallo studio della congiunzione e della disgiunzione erano le medesime
di quelle godute dalle operazioni di somma e prodotto in un algebra in cui le variabili potevano
assumere solo i valori numerici 0 e 1. Costruì quindi, un sistema algebrico comprendente le
operazioni di somma, prodotto, complementazione e sottrazione, suscettibili di una duplice
interpretazione: puramente logica (le variabili erano simboli per classi) o numerica (0 e 1). Il
calcolo booleano rendeva, così, conto della logica delle classi e della logica delle proposizioni
(in questo caso i valori 0 e 1 equivalevano rispettivamente ai valori falso e vero).
Boole espose le sue concezioni logiche in L’analisi matematica della logica (1847), dove
considerò la logica come una branca della matematica e come una disciplina che era diventata
scientifica nel momento in cui era stata matematizzata. Il modo booleano di intendere la logica
sarà mantenuto fino ai nostri giorni, esso, come si è potuto riscontrare, non ha legami né con
l’antichità né con la tradizione medioevale. La nuova logica è “matematica” non solo perché fa
uso di un apparato simbolico e di metodi matematici, ma anche perché si rivolge all’analisi di
questioni e problemi interni alla matematica. Dopo Boole, con Gottlob Frege (1848-1925) ancor
di più la logica si vedrà conferito l’aspetto che oggi le è proprio, portando anche le più pure
speculazioni filosofiche intorno ad essa a svolgersi all’interno di competenze tecniche specifiche
di logica matematica.
10