Prova del 21-2-2017

PROVA SCRITTA DI ELETTROTECNICA (21 FEBBRAIO 2017)
Prof. Luigi Verolino
Cognome:
Nome:
Matricola:
 è l’ultima cifra non nulla della matricola:
Esercizio 1
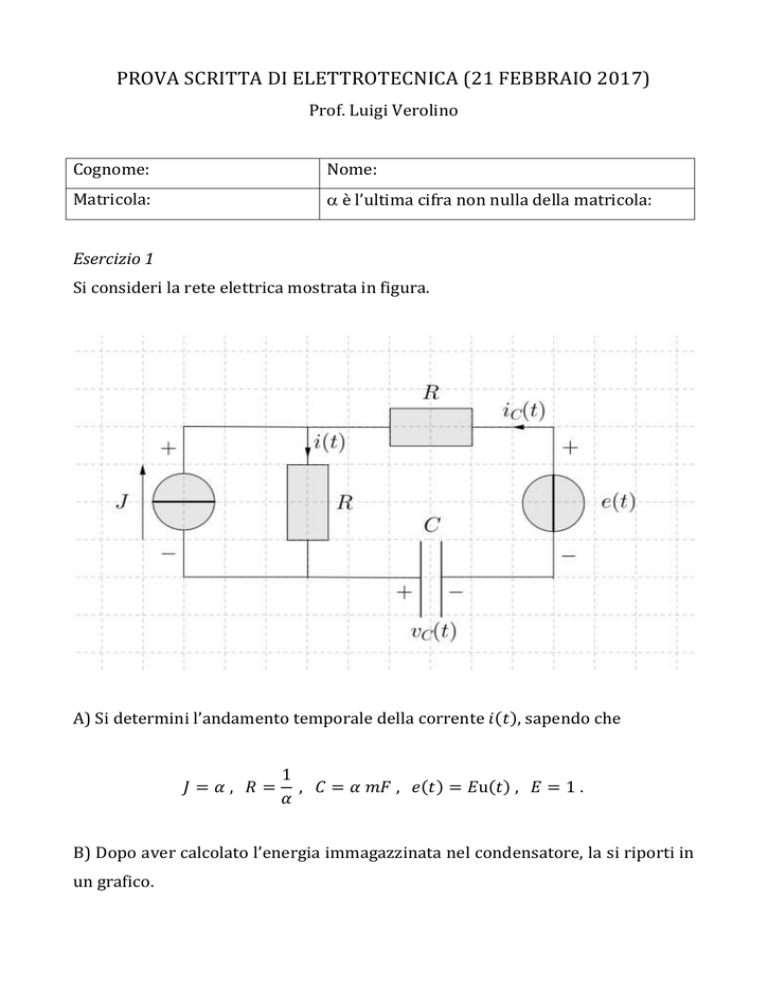
Si consideri la rete elettrica mostrata in figura.
A) Si determini l’andamento temporale della corrente 𝑖(𝑡), sapendo che
𝐽=𝛼, 𝑅=
1
, 𝐶 = 𝛼 𝑚𝐹 , 𝑒(𝑡) = 𝐸u(𝑡) , 𝐸 = 1 .
𝛼
B) Dopo aver calcolato l’energia immagazzinata nel condensatore, la si riporti in
un grafico.
Esercizio 2
Si verifichi che 1 + 𝑖 è una radice del polinomio
𝑧 4 − 5𝑧 3 + 10𝑧 2 − 10𝑧 + 4
e si calcolino poi tutte le altre radici.
Valutazione della prova scritta
Esercizio 1
Esercizio 2
Complessivo
Valutazione della prova orale
Domanda 1
Domanda 2
Domanda 3
Voto finale
Esercizio 1
A) Per 𝑡 < 0, la rete è a regime ed il condensatore si comporta come un circuito
aperto, per cui
𝑖(𝑡) = 𝐽 = 𝛼 , 𝑣𝐶 (𝑡) = −𝑅𝐽 = −1 .
Discende allora il valore della condizione iniziale
𝑣𝐶 (0) = −𝑅𝐽 = −1 .
Per 𝑡 > 0, la rete è descritta dalle tre equazioni
𝑅𝑖𝐶 + 𝑅𝑖 + 𝑣𝐶 = 𝑒 ,
𝑑𝑣
{ 𝑖𝐶 = 𝐶 𝐶 ,
𝑑𝑡
𝑖 = 𝐽 + 𝑖𝐶 .
Eliminando le due correnti, che non sono variabili di stato, si ottiene l’unica
equazione differenziale
𝑑𝑣𝐶 𝑣𝐶 𝐸u(𝑡) − 𝑅𝐽
+
=
,
𝑑𝑡
𝜏
𝜏
in cui è stata utilizzata la costante di tempo
𝜏 = 2𝑅𝐶 = 2 𝑚𝑠 .
Dal momento in ogni istante di tempo 𝑡 > 0 risulta
𝐸u(𝑡) − 𝑅𝐽 = 0 ,
è possibile scrivere il seguente problema di Cauchy
𝑑𝑣𝐶 𝑣𝐶
+
=0,
{ 𝑑𝑡
𝜏
𝑣𝐶 (0) = −𝑅𝐽 = −1 ,
la cui soluzione è immediata
𝑣𝐶 (𝑡) = −𝑅𝐽 e−𝑡/𝜏 = −e−𝑡/𝜏 .
Pertanto, la corrente 𝑖(𝑡) risulta pari a
𝑖(𝑡) = 𝐽 + 𝐶
𝑑𝑣𝐶
𝐽
𝛼
= 𝐽 + e−𝑡/𝜏 = 𝛼 + e−𝑡/𝜏 .
𝑑𝑡
3
2
In definitiva, la corrente richiesta vale
𝛼,
𝑡 <0,
𝛼
𝑖(𝑡) = {
𝛼 + e−𝑡/𝜏 , 𝑡 > 0 .
2
Vale la pena notare che, non essendo variabile di stato, questa corrente non è
continua in 𝑡 = 0.
B) L’energia immagazzinata nel condensatore è pari a
1
𝑈(𝑡) = 𝐶𝑣𝐶2 (𝑡) = 𝑈0 e−2𝑡/𝜏 ,
2
in cui, per brevità, si è posto
1
𝛼
𝑈0 = 𝐶𝑅2 𝐽2 = 𝑚𝐽 .
2
2
L’andamento di questa energia, in ogni istante di tempo, è riportato nella figura
che segue.
Esercizio 2
Introdotta la funzione polinomiale
𝑃(𝑧) = 𝑧 4 − 5𝑧 3 + 10𝑧 2 − 10𝑧 + 4 ,
se il numero complesso 1 + 𝑖 è una radice, allora deve essere
𝑃(1 + 𝑖) = 0 .
Pertanto, posto
𝑧 = 1 + 𝑖 = √2 e𝑖𝜋/4 ,
sostituendo nella funzione polinomiale, si può scrivere
𝑃(1 + 𝑖) = 4 e𝑖𝜋 − 10√2 e3𝑖𝜋/4 + 20 e𝑖𝜋/2 − 10√2 e𝑖𝜋/4 + 4 .
Ebbene, dal momento che
e𝑖𝜋 = −1 , √2 e3𝑖𝜋/4 = −1 + 𝑖 , e𝑖𝜋/2 = 𝑖 , √2 e𝑖𝜋/4 = 1 + 𝑖 ,
l’espressione precedente diventa
𝑃(1 + 𝑖) = −4 − 10(−1 + 𝑖) + 20𝑖 − 10(1 + 𝑖) + 4 = 0 ,
cioè la tesi desiderata, per cui 1 + 𝑖 è radice del polinomio assegnato.
Orbene, essendo il polinomio a coefficienti reali, discende che anche 1 − 𝑖 è una
radice, sicché il trinomio
𝐷(𝑧) = (𝑧 − 1 − 𝑖)(𝑧 − 1 + 𝑖) = (𝑧 − 1)2 + 1 = 𝑧 2 − 2𝑧 + 2
risulta divisore del polinomio 𝑃(𝑧). Eseguendo la divisione, si ottiene
𝑃(𝑧) 𝑧 4 − 5𝑧 3 + 10𝑧 2 − 10𝑧 + 4
=
= 𝑧 2 − 3𝑧 + 2 ,
2
𝐷(𝑧)
𝑧 − 2𝑧 + 2
per cui le rimanenti due radici si ottengono risolvendo l’equazione quadratica
𝑧 2 − 3𝑧 + 2 = 0 → 𝑧1,2 = 1, 2 .
Riepilogando, si può affermare che, in forza del Teorema Fondamentale
dell’Algebra, il polinomio assegnato, essendo di quarto grado, presenta quattro
radici. Precisamente, due di queste radici sono reali e distinte e valgono
𝑧1,2 = 1, 2 ,
le altre due sono complesse e coniugate e pari a
𝑧3,4 = 1 ± 𝑖 .
Per maggiore chiarezza, la figura che segue rappresenta le quattro radici nel
piano complesso di Argand-Gauss.
Jean-Robert Argand è stato un matematico svizzero non professionista.
Nel 1806, mentre era il gestore di una libreria a Parigi, pubblicò a proprie spese
un libro in cui veniva esposta l’idea dell’interpretazione geometrica dei numeri
complessi. Grazie a questo studio, a lui ed a Carl Friedrich Gauss è stato
intitolato il piano complesso, un grafico che rappresenta in ascissa la parte reale
del numero complesso ed in ordinata la parte immaginaria, trasformando in
questo modo un numero complesso in un vettore. Il concetto del piano
complesso consente una interpretazione geometrica dei numeri complessi:
questi si sommano come vettori, mentre la loro moltiplicazione può essere
geometricamente espressa usando le coordinate polari, dove il modulo del
prodotto è il prodotto dei moduli dei fattori e l’argomento del prodotto, cioè
l’angolo rispetto all’asse reale, è la somma degli angoli dei fattori. I diagrammi
nel piano complesso sono frequentemente usati per mostrare la posizione dei
poli o di zeri di una funzione nel piano complesso.
Jean-Robert Argand
Ginevra, 18 luglio 1768 – Parigi, 13 agosto 1822
Tra i suoi contributi occorre anche ricordare una dimostrazione, non
completamente corretta, del Teorema Fondamentale dell’Algebra. Argand
sembra essere stato il primo a trattare il caso in cui i coefficienti possono anche
essere numeri complessi.