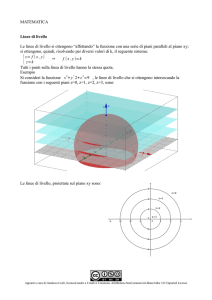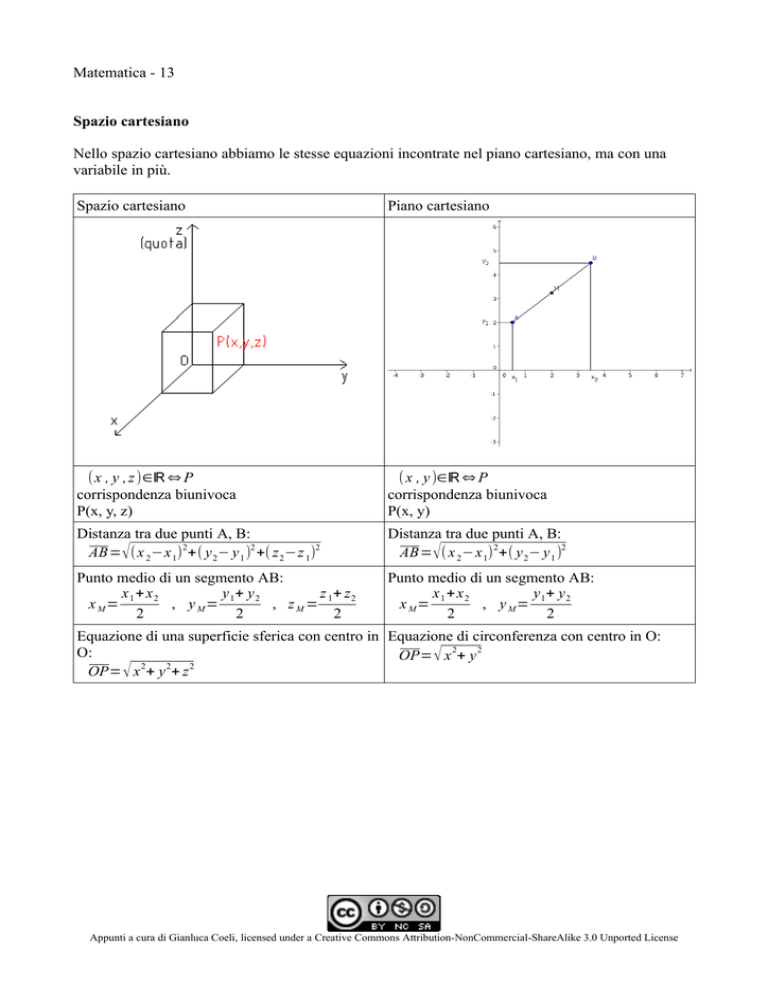
Matematica - 13
Spazio cartesiano
Nello spazio cartesiano abbiamo le stesse equazioni incontrate nel piano cartesiano, ma con una
variabile in più.
Spazio cartesiano
Piano cartesiano
(x , y , z )∈ℝ ⇔ P
corrispondenza biunivoca
P(x, y, z)
( x , y )∈ℝ ⇔ P
corrispondenza biunivoca
P(x, y)
Distanza tra due punti A, B:
AB=√(x 2−x 1) 2+( y 2− y 1 )2 +( z 2−z 1)2
Distanza tra due punti A, B:
AB=√( x 2−x 1) 2+( y 2− y 1 )2
Punto medio di un segmento AB:
x1+ x2
y +y
z +z
, y M= 1 2 , z M = 1 2
x M=
2
2
2
Punto medio di un segmento AB:
x1+ x2
y +y
, y M= 1 2
x M=
2
2
Equazione di una superficie sferica con centro in Equazione di circonferenza con centro in O:
O:
OP= √ x 2+ y 2
2
2
2
OP= √ x + y + z
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
Equazione generale di una superficie sferica:
PC =r=√ ( x−α) 2+( y−β) 2+(z −γ)2
2
2
2
2
r =( x−α) +( y−β) +( z −γ)
x 2 + y 2 + z 2+ ax +by +cz + d =0
con:
a=−2 α , b=−2β , c=−2 γ e
d =α 2 +β2+ γ 2−r 2
Equazione generale di una circonferenza:
PC =r=√( x−α) 2+( y−β) 2
2
2
2
r =( x−α) +( y−β) e da qui:
x 2 + y 2 + ax+ by+ c=0
con:
a=−2 α , b=−2β , c=α 2 +β2−r 2
Equazione del piano nello spazio cartesiano
Per analogia con l'equazione della retta sul piano cartesiano ax +by +c=0 , nello spazio cartesiano
si ha:
ax +by +cz + d =0
Le soluzioni di quest'equazione sono infinite, ed ogni soluzione è una terna di numeri (x,y,z).
I piani si indicano con le lettere greche α ,β , γ , ...
Si ha che:
- per un punto passano infiniti piani;
- per due punti passano9 infiniti piani;
- per tre punti non allineati passa un solo piano.
Piani particolari
- se d=0 → ax +by + cz=0 è l'equazione di infiniti piani che passano da O
- piani coordinati:
* piano xy → equazione z=0
* piano xz → equazione y=0
* piano yz → equazione x=0
Piani paralleli ai piani coordinati:
|| xy → ad esempio z=1; l'equazione generale è z=k
|| xz → y=k
|| yz → x=k
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
Equazione della retta
Una retta nello spazio cartesiano risulta dall'intersezione di due piani:
α : ax +by +cz + d =0
β : a 1 x +b 1 y +c 1 z +d 1=0
l'equazione della retta si ottiene da r =α∧β , cioè è il seguente sistema:
ax+ by +cz +d=0
a 1 x+ b1 y+c 1 z+ d=0
{
Equazione di rette particolari:
- equazione dell'asse x: metto a sistema il piano xy e il piano xz:
y=0
z=0
- equazione dell'asse y: metto a sistema il piano xy e il piano yz:
x=0
z=0
- equazione dell'asse z: metto a sistema il piano xz e il piano yz:
x=0
y=0
{
{
{
Esercizio
Determinare l'intersezione del piano
3x−4y +2z−12=0
con asse x z=0
y=0
3x−4y +2z−12=0
con asse y x=0
z=0
3x−4y +2z−12=0
con asse z x=0
y=0
{
{
{
α : 3x−4y + 2z−12=0
3x−12=0
3x=12
z=0
z=0
y=0
y=0
−4y−12=0
−4y=12
x=0
x=0
z=0
z=0
2z−12=0
2z=12
x=0
x=0
y=0
y=0
{
{
{
{
{
{
e gli assi cartesiani
x=4
P (4,0 ,0)
z=0
y=0
y=−3
Q(0,−3,0)
x=0
z=0
z=6
R(0,0 ,6)
x=0
y=0
{
{
{
P, Q, R sono i punti di intersezione del piano. Sono punti non allineati.
Verifica: dati i 3 punti P, Q, R, determinare l'equazione del piano
L'equazione generale è: ax +by +cz + d =0
d
a=−
4
4a +d =0
4a=−d
d
sostituisco questi valori nell'equazione generale
b=
−3b+ d =0
−3b=−d
3
6c+d=0
6c=−d
d
c=−
6
ax +by + cz +d =0 semplifico dividendo tutto per d
1
1
1
− x + y− z +1=0 faccio il minimo comune denominatore
4
3
6
−3x +4y−2z+ 12 0
=
semplifico il denominatore
12
12
{
{
{
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
−3x+ 4y−2z +12=0 infine moltiplico per -1
3x−4y + 2z−12=0 c.v.d.
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License