CorsI di Laurea in
Ingegneria Aereospaziale-Meccanica-Energetica
FONDAMENTI DI CHIMICA
Docente: Cristian Gambarotti
Esercitazione del 05/10/2010
ARGOMENTI TRATTATI DURANTE LA LEZIONE
• Esercizi di riepilogo su stechiometria
• Concetto di densità di una sostanza
• Percentuale in peso, in volume, frazione molare
• Unità di misura della concentrazione – molarità e molalità
Un idrocarburo, bruciato all’aria produce 3,669g di CO2 e 1,751g di acqua. Calcolare la
formula empirica del composto.
Se il peso molecolare è pari a 86,0g/mol calcolare anche la formula molecolare.
Gli idrocarburi sono composti formati esclusivamente da C e H
Es.:
CH4 (metano), C2H6 (etano), C2H4 (etilene o etene), C6H6 (benzene)
Sia CxHy la formula molecolare dell’idrocarburo incognito con x e y da determinare
Scriviamo la reazione di combustione:
C x H y + O2 → CO2 + H 2O
che deve essere opportunamente bilanciata:
y
C x H y + O2 → xCO2 + H 2O
2
Bilancio su C e H
y⎞
y
⎛
C x H y + ⎜ x + ⎟O2 → xCO2 + H 2 O
4⎠
2
⎝
Bilancio su O
y⎞
y
⎛
C x H y + ⎜ x + ⎟O2 → xCO2 + H 2 O
4⎠
2
⎝
Calcoliamo le moli di CO2 e di acqua prodotte:
nCO2 = n.moli CO2 =
massa CO2
3,669 g
=
= 8,339 × 10 − 2 mol
M CO2
44 g / mol
nH 2O = n.moli H 2O =
massa H 2O
1,751g
=
= 9,728 × 10 − 2 mol
M H 2O
18 g / mol
x
In base alla stechiometria della reazione per ogni mole di acqua si producono y moli di CO2
2
QUINDI il rapporto tra le moli di CO2 e acqua prodotte deve essere uguale al
corrispondente rapporto dei coefficienti stechiometrici
n.molCO2 0,08339
x
y
7
=
≅ 0,857 =
⇒ x = 0,4285 ⋅ y ⇔ = 2,334 ≅
y
n.molH 2O 0,09728
x
3
2
La formula minima è: C3H7
Per calcolare la formula molecolare occorre conoscere la massa molare
Pertanto si ha:
formula della massa molare
x ⋅12 + y ⋅1 = 86
MC
X=6
MH
y=14
MCxHy
y 7
=
x 3
x ⋅12 + y ⋅1 = 86
La formula molecolare è C6H14
Gli alcani sono idrocarburi saturi che hanno formula generale CnH2n+2
CH4 (metano), C2H6 (etano), C3H8 (propano), C4H10 (butano), C5H12 (pentano), C6H14 (esano)
ALCUNE CONSIDERAZIONI
L’esercizio presentato oltre ad avere un contenuto didattico (n. moli, bilanciamento
reazione f. minima, f.molecolare, impostazione matematica del problema) rappresenta
un esempio di indagine sperimentale.
1. Si ha a disposizione un composto incognito (però si sa già che è un idrocarburo)
2. Si brucia il composto ottenendo solo H2O e CO2
Î
Siamo sicuri?
3. Si pesa l’acqua e la CO2
Î
Come?
4. Si misura la massa molare del composto
Î
Spettrometro di massa
L’informazione 2. non è sufficiente per stabilire che il composto è un idrocarburo.
Cioè, è vero che la combustione completa di ogni idrocarburo fornisce CO2 e acqua.
Ma non è vero che acqua e CO2 derivano esclusivamente dalla combust. completa di idrocarburi.
Es.
C2H5OH + 3O2 Æ 2CO2 +3H2O
(l’etanolo non è un idrocarburo)
Per essere sicuri di avere ottenuto solo CO2 e acqua (combustione completa) la
reazione deve avvenire in eccesso di O2.
Se il processo avviene in difetto di O2 si può produrre anche monossido di carbonio
(CO)
Es. Supponiamo di volere bruciare 1mole di metano
CH4+2O2ÆCO2+2H2O
2moli di O2 per ogni mole di metano
Se si alimentasse un numero di moli di O2 inferiore a 2 per ogni mole di metano
potrebbe verificarsi la seguente reazione competitiva:
CH4+3/2O2ÆCO+2H2O
1,5moli di O2 per ogni mole di metano
Nell’incertezza si alimenta al reattore un numero di moli di O2 per ogni mole di CH4 >2
Come si pesa l’acqua e la CO2?
H2O e CO2 gas + O2 residuo
Recupero acqua
CO2 gas +
O2 residuo
condensazione oppure
reazione chimica con
substrato solido (es. P2O5)
CxHy + O2 (in eccesso)
Recupero CO2
solo O2
residuo
reazione chimica con una
sostanza basica (es. ossido
di calcio, CaO, oppure
idrossido di sodio, NaOH)
P2O5+3H2OÆ2H3PO4
CO2+CaOÆCaCO3
La differenza tra il
peso finale e il peso
iniziale fornisce la
quantità di acqua
prodotta
La differenza tra il
peso finale e il peso
iniziale fornisce la
quantità di CO2
prodotta
Calcolare la quantità di bromobenzene (C6H5Br) teoricamente ottenibile da 78,0 g di
benzene (C6H6) e 120,0 g di Br2.
Calcolare, inoltre, la resa percentuale se si ottengono 85,6 g di C6H5Br
C6H6(l) + Br2(l) Æ C6H5Br(l) + HBr(g)
n.moli benzene =
n.moli bromo =
massa benz
78,0g
=
= 1mol
M benz
78g/mol
massa bromo
120 g
=
= 0,751mol
M bromo
159,8 g / mol
n.Moli C6H5Br teoriche = n.moli Br2=0,751
Benzene in eccesso
Br2 reagente limitante
Massa C6H5Br teorica=
(0,751mol)x(156,9g/mol)=117,83g
massa C 6 H 5 Br effettiva
85,6 g
Resa% =
× 100 =
×100 = 72,6%
massa C 6 H 5 Br teorica
117,8 g
DENSITÀ
Massa di sostanza contenuta in un volume unitario
d=
massa
volume
Unità di misura: g/cm3, g/mL, kg/L, kg/dm3, kg/m3
Può essere definita qualunque sia lo stato di aggregazione della sostanza
(solido, liquido, gassoso)
Dipende dalla temperatura – La densità dei gas dipende anche dalla pressione
Es. acqua liquida
benzina
Aria (gas) a 0°C e 1atm
1g/cm3 = 1g/mL = 1kg/dm3 = 1kg/L = 1000kg/m3
~720kg/m3
1,29kg/m3
Acciaio
7850kg/m3
Alluminio
2700kg/m3
Fibre di carbonio
1800kg/m3
mercurio (metallo liquido a temp.ambiente):
13600kg/m3 = 13,6g/mL
~ 1000 più piccola della d dell’acqua
Percentuale in peso, percentuale in volume e frazione molare
Consideriamo una miscela costituita, per semplicità, da due sole sostanze A e B
Percentuale in peso
%WA =
mA
m
×100 = A ×100
m A + mB
mTOT
%WB =
mB
m
×100 = B ×100
m A + mB
mTOT
%WA + %WB = 100
m A = massa A
mB = massa B
Percentuale in volume
VA
V
% =
× 100 = A × 100
V A + VB
VTOT
A
V
%VB =
VB
V
× 100 = B × 100
V A + VB
VTOT
%VA + %VB = 100
VA = Volume A
VB = Volume B
Frazione molare
nA
n
xA =
= A
n A + n B nTOT
n A = numero moli A
nB = numero moli B
xB =
nB
n
= B
n A + n B nTOT
x A + xB = 1
Esempi
500g di una soluzione acquosa di NaCl al 10% in peso
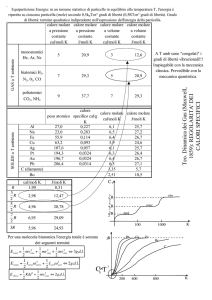
1ton di Combustibile Derivato dai Rifiuti (C.D.R.)
Ha la seguente composizione (in peso)
Materie plastiche: 17%
Carta e cartone: 67%
Residui di tessuti: 10%
Gomma, residui di legno e pellame: 5%
Scarti metallici e vetrosi: 1%
50 g NaCl disciolti in 450g di
acqua
670kg carta e cartone
170kg materie plastiche
.
.
.
1 bottiglia di birra (66cL) ha un contenuto di
alcol pari al 4,5%vol
(66cL)x0,045=2,97cL (29,7mL =
0,0297L) alcol
Una miscela gassosa costituita da 3moli N2,
8moli Ar e 5mol O2
fraz.molare N2:
fraz.molare Ar:
fraz.molare O2:
3/16=0,1875
8/16=0,5
5/16=0,3125
Si consideri la reazione di produzione dell’etanolo a partire dal glucosio:
C6 H12O6 (aq ) → 2 C2 H 5OH (aq ) + 2 CO2 ( g )
a)
b)
Quanto alcool etilico (in kg) si produce facendo fermentare 100 kg di materiale contenente
il 90% in peso di glucosio?
Quanti litri di etanolo si ottengono sapendo che la densità dell’alcool è pari a 0,785 kg/l?
c)
Quanto vale la resa del processo se si ottengono 49,7 L di alcool?
100 kg al 90% in peso di glucosio
n.moli glucosio
90 kg di glucosio
90 kg
= 0,5 kmol = 500mol
kg
180
kmol
1kmol alcol prodotto (teoricamente)
⎞⎟ = 46kg
massa alcol = (1kmol) ⋅ ⎛⎜ 46 kg
kmol ⎠
⎝
densità = d =
massa (kg)
volume (L)
resa(%) =
VETOH =
massa ETOH
46 kg
=
= 58,6L
kg
d ETOH
0,785
L
massa ETOH
n ETOH
VETOH
49,7 L
⋅
100
=
⋅
100
=
⋅
100
=
⋅100 = 84,8%
TEOR
TEOR
TEOR
58,6 L
massa ETOH
n ETOH
VETOH
Dalla combustione completa di 102g di una miscela di propano, C3H8, e butano, C4H10 si
liberano 162g di acqua.
Scrivere e bilanciare le equazioni di reazione e determinare la composizione ponderale della
miscela.
C3 H 8 + O2 → CO2 + H 2O
C3 H 8 + 5O2 → 3CO2 + 4 H 2O
C4 H10 + O2 → CO2 + H 2O
C 4 H 10 +
1)
13
O2 → 4CO2 + 5 H 2 O
2
2)
Due sono le informazioni a disposizione: la massa di miscela e la massa di acqua prodotta
m TOT
COMB = massa tot. combustibile = massa(C3 H 8 ) + massa(C 4 H10 ) = 102g
n C3H8 ⋅ 44 + n C 4 H10 ⋅ 58 = 102 (g)
MC3H8
m TOT
H 2 O = massa tot. acqua = massa acqua (1) + massa acqua (2) = 162g
(n
C3H8
MC4H10
)
⋅ 4 + n C 4 H10 ⋅ 5 ⋅18 = 162 (g)
MH2O
n C3H8 = 1 n C 4 H10 = 1
m C3H8 = 44 g
m C 4 H10 = 58 g
La composizione ponderale della miscela è infine data da:
% W C3H 8 = 100 ×
44g
= 43.1%
102g
% W C 4 H10 = 100 ×
58g
= 56.9%
102g
Quanti litri di H2SO4 al 65% peso (d=1,55g/mL) si possono ottenere da 100kg di pirite (FeS2)
considerando una resa del 90% (con rif.alla reazione (1))
Le reazioni da considerare sono le seguenti:
4FeS2(s)+11 O2(g) Æ 2Fe2O3(s) + 8SO2(g)
(1)
2SO2(g) + O2(g) Æ 2SO3(g)
(2)
SO3(g) + H2O(g) Æ H2SO4(aq)
(3)
Gas insolubili (N2, O2 residuo)
4FeS2(s)+11 O2(g) Æ 2Fe2O3(s) + 8SO2(g)
~900°C
aria
SO2
2SO2(g) + O2(g) Æ 2SO3(g)
~400°C
SO3
soluz. acquosa
H2SO4 (oleum)
acqua
FeS2
ossidazione SO2
“arrostimento” piriti
aria
SO3(g) + H2O(g) Æ H2SO4(aq)
4FeS2(s)+11 O2(g) Æ 2Fe2O3(s) + 8SO2(g)
n.moli pirite =
2SO2(g) + O2(g) Æ 2SO3(g)
SO3(g) + H2O(g) Æ H2SO4(aq)
massa pirite
100kg
=
= 0,834kmol
M FeS2
119,98kg/kmol
8
n.moli teoriche SO 2 = × (0,834kmol) = 1,668kmol
4
(2moli di SO2 per ogni mole di FeS2)
n.moli effettive SO 2 = (1,668kmol )× resa% = (1,668kmol )× (0,9 ) = 1,501kmol
Dalla 2) si ha:
n.moli SO 3 = n.moli SO 2 = 1,501kmol (1moli di SO3 per ogni mole di SO2)
Dalla 3) infine:
⎞⎟ = 147,3kg
massa H 2SO 4 puro = (1,501kmol )× ⎛⎜ 98,1 kg
kmol
⎝
⎠
n.moli H 2SO 4 = n.moli SO 3 = 1,501kmol
QUINDI
massa H 2SO 4 al 65% in peso =
147,3kg
= 226,6kg
0,65
volume H 2SO 4 al 65% in peso =
226,6kg
= 146,2L
kg
1,55
L
Misure di concentrazione – molarità e molalità
n.moli Soluto
M ≡ molarità =
volume Soluzione(L)
m ≡ molalità =
n.moli Soluto
massa Solvente (kg)
Soluzione NaCl in acqua 1M (leggi 1 molare):
1mole NaCl (58,5grammi) in acqua fino ad
avere 1litro di soluzione
Soluzione NaCl in acqua 1m (leggi 1 molale):
1mole NaCl (58,5grammi) in 1kg acqua
Calcolare il volume di una soluzione di HCl al 38% in peso (d=1,19g/mL)
necessario per preparare 1,5L di soluzione 4,0M.
Qual è la concentrazione molare della soluzione al 38%?
n.moli soluto (HCl) nel matraccio B=(1,5L) x (4,0moli/L)=6moli
6moli HCl
219 grammi HCL
La soluzione nel matraccio A
è al 38% in peso
(6moli) x (36,5g/mol)
Massa HCl (38%W) prelevata da A vale:
219grammi/0,38=576,3grammi
QUINDI
Il volume prelevato da A vale:
(576,3grammi)/densità=(576,3grammi)/(1,19g/mL)=484,3mL
1kg di soluzione al 38% contiene 380 grammi di HCl cioè 10,41 moli di HCl
1kg di soluzione al 38% ha un volume di 0,84L
(1kg/densità)
La concentrazione molare della soluzione al 38% è pari a: (10,41mol)/(0,84L)=12,4M