istituto " giordano bruno "

L I C E O S T A T A L E “FARNESINA”
Sezione Scientifica-Sezione Musicale
ROMA
ANNO SCOLASTICO 2016-2017
PROGRAMMAZIONE DISCIPLINARE D'ISTITUTO
LINEE GENERALI E COMPETENZE
Disciplina: MATEMATICA
Indirizzo: Scientifico
Al termine del percorso del liceo scientifico lo studente conoscerà i concetti e i metodi
elementari della matematica, sia interni alla disciplina in sé considerata, sia rilevanti per la
descrizione e la previsione di fenomeni, in particolare del mondo fisico. Egli saprà inquadrare le
varie teorie matematiche studiate nel contesto storico entro cui si sono sviluppate e ne
comprenderà il significato concettuale.
Lo studente avrà acquisito una visione storico-critica dei rapporti tra le tematiche principali del
pensiero matematico e il contesto filosofico, scientifico e tecnologico. In particolare, avrà
acquisito il senso e la portata dei tre principali momenti che caratterizzano la formazione del
pensiero matematico: la matematica nella civiltà greca, il calcolo infinitesimale che nasce con
la rivoluzione scientifica del Seicento e che porta alla matematizzazione del mondo fisico, la
svolta che prende le mosse dal razionalismo illuministico e che conduce alla formazione della
matematica moderna e a un nuovo processo di matematizzazione che investe nuovi campi
(tecnologia, scienze sociali, economiche, biologiche) e che ha cambiato il volto della
conoscenza scientifica.
Di qui i gruppi di concetti e metodi che saranno obiettivo dello studio:
1) gli elementi della geometria euclidea del piano e dello spazio entro cui prendono forma i
procedimenti
caratteristici
del
pensiero
matematico
(definizioni,
dimostrazioni,
generalizzazioni, assiomatizzazioni);
2) gli elementi del calcolo algebrico, gli elementi della geometria analitica cartesiana, una
buona conoscenza delle funzioni elementari dell’analisi, le nozioni elementari del calcolo
differenziale e integrale;
3) gli strumenti matematici di base per lo studio dei fenomeni fisici, con particolare riguardo al
calcolo vettoriale e alle equazioni differenziali, in particolare l’equazione di Newton e le sue
applicazioni elementari;
4) la conoscenza elementare di alcuni sviluppi della matematica moderna, in particolare degli
elementi del calcolo delle probabilità e dell’analisi statistica;
5) il concetto di modello matematico e un’idea chiara della differenza tra la visione della
matematizzazione caratteristica della fisica classica (corrispondenza univoca tra matematica e
natura) e quello della modellistica (possibilità di rappresentare la stessa classe di fenomeni
mediante differenti approcci);
6) costruzione e analisi di semplici modelli matematici di classi di fenomeni, anche utilizzando
strumenti informatici per la descrizione e il calcolo;
7) una chiara visione delle caratteristiche dell’approccio assiomatico nella sua forma moderna e
delle sue specificità rispetto all’approccio assiomatico della geometria euclidea classica;
8) una conoscenza del principio di induzione matematica e la capacità di saperlo applicare,
avendo inoltre un’idea chiara del significato filosofico di questo principio (“invarianza delle leggi
del pensiero”), della sua diversità con l’induzione fisica (“invarianza delle leggi dei fenomeni”) e
di come esso costituisca un esempio elementare del carattere non strettamente deduttivo del
ragionamento matematico.
Questa articolazione di temi e di approcci costituirà la base per istituire collegamenti e
confronti concettuali e di metodo con altre discipline come la fisica, le scienze naturali e sociali,
la filosofia e la storia.
Al termine del percorso didattico lo studente avrà approfondito i procedimenti caratteristici del
pensiero matematico (definizioni, dimostrazioni, generalizzazioni, formalizzazioni), conoscerà
le metodologie di base per la costruzione di un modello matematico di un insieme di fenomeni,
saprà applicare quanto appreso per la soluzione di problemi, anche utilizzando strumenti
informatici di rappresentazione geometrica e di calcolo. Tali capacità operative saranno
particolarmente accentuate nel percorso del liceo scientifico, con particolare riguardo per quel
che riguarda la conoscenza del calcolo infinitesimale e dei metodi probabilistici di base.
Gli strumenti informatici oggi disponibili offrono contesti idonei per rappresentare e manipolare
oggetti matematici. L'insegnamento della matematica offre numerose occasioni per acquisire
familiarità con tali strumenti e per comprenderne il valore metodologico. Il percorso, quando
ciò si rivelerà opportuno, favorirà l’uso di questi strumenti, anche in vista del loro uso per il
trattamento dei dati nelle altre discipline scientifiche. L’uso degli strumenti informatici è una
risorsa importante che sarà introdotta in modo critico, senza creare l’illusione che essa sia un
mezzo automatico di risoluzione di problemi e senza compromettere la necessaria acquisizione
di capacità di calcolo mentale.
L’ampio spettro dei contenuti che saranno affrontati dallo studente richiederà che l’insegnante
sia consapevole della necessità di un buon impiego del tempo disponibile. Ferma restando
l’importanza dell’acquisizione delle tecniche, verranno evitate dispersioni in tecnicismi ripetitivi
o casistiche sterili che non contribuiscono in modo significativo alla comprensione dei problemi.
L'approfondimento degli aspetti tecnici, sebbene maggiore nel liceo scientifico che in altri licei,
non perderà mai di vista l’obiettivo della comprensione in profondità degli aspetti concettuali
della disciplina. L’indicazione principale è: pochi concetti e metodi fondamentali, acquisiti in
profondità.
Finalità:
Lo studio della matematica promuove:
 lo sviluppo di capacità intuitive e logiche
 la capacità di usare procedimenti euristici
 la maturazione dei processi di astrazione e di formazione dei concetti
 la capacità di ragionare induttivamente e deduttivamente
 l’abitudine alla precisione del linguaggio
 lo sviluppo delle attitudini analitiche e sintetiche
 l’acquisizione di strumenti intellettivi che possano essere utilizzati nelle
successive scelte di studio e di lavoro
 la consapevolezza dell’importanza sociale ed economica delle discipline
scientifiche
Obiettivi: Conoscenze

i contenuti delle linee guida ministeriali
Competenze
 utilizzare le tecniche e le procedure del calcolo aritmetico ed algebrico
rappresentandole anche in forma grafica
 confrontare e analizzare figure geometriche individuando invarianti e
relazioni
 individuare strategie appropriate per la soluzione dei problemi
 analizzare dati e interpretarli sviluppando deduzioni e ragionamenti
sugli stessi anche con l’ausilio di rappresentazioni grafiche, usando
consapevolmente gli strumenti di calcolo e le potenzialità offerte da
applicazioni di tipo informatico
 giustificare opportunamente le scelte effettuate nella risoluzione dei
problemi esponendo con proprietà di linguaggio le conoscenze utilizzate
Capacità
 capacità di interpretare un testo di matematica
 capacità di intuizione, astrazione, deduzione, formalizzazione
 capacità di collegare gli argomenti studiati e di rielaborare i procedimenti
risolutivi.
Contenuti:
ARTICOLAZIONE TEMPORALE DI MASSIMA DEI CONTENUTI PER LE CLASSI
PRIME DEL LICEO SCIENTIFICO
Periodo
Conoscenze
Numeri naturali
Trimestre
Numeri interi
Trimestre
Abilità
 Calcolare il valore di un’espressione
numerica
 Passare dalle parole ai simboli e
viceversa
 Applicare le proprietà delle
operazioni e delle potenze
 Sostituire alle lettere i numeri e
risolvere espressioni letterali
 Scomporre un numero naturale in
fattori primi
 Calcolare MCD e mcm di numeri
naturali
 Calcolare il valore di un’espressione
numerica
 Applicare le proprietà delle potenze
 Tradurre una frase in un’espressione,
sostituire alle lettere numeri interi e
risolvere espressioni letterali
 Risolvere problemi
Numeri razionali assoluti
Trimestre
Numeri razionali e numeri reali
Trimestre
Insiemi e logica
Trimestre
Relazioni e funzioni
Trimestre
Monomi
Trimestre
Polinomi
Trimestre
 Semplificare espressioni con le
frazioni
 Tradurre una frase in un’espressione e
sostituire numeri razionali alle lettere
 Risolvere problemi con percentuali e
proporzioni
 Trasformare numeri decimali in
frazioni
 Semplificare espressioni con numeri
razionali relativi e potenze con
esponente negativo
 Riconoscere numeri razionali e
irrazionali
 Eseguire calcoli approssimati
 Stabilire l’ordine di grandezza di un
numero
 Risolvere problemi utilizzando la
notazione scientifica
 Eseguire calcoli approssimati e con
potenze di 10
 Rappresentare un insieme e
riconoscere i sottoinsiemi di un
insieme
 Eseguire operazioni tra insiemi
 Determinare la partizione di un
insieme
 Risolvere problemi utilizzando
operazioni tra insiemi
 Rappresentare una relazione
 Riconoscere una relazione di
equivalenza e determinare l’insieme
quoziente
 Riconoscere una relazione d’ordine
 Rappresentare una funzione e stabilire
se è iniettiva, suriettiva o biiettiva
 Disegnare il grafico di una funzione
 Riconoscere un monomio e stabilirne
il grado
 Sommare algebricamente monomi
 Calcolare prodotti, potenze e
quozienti di monomi
 Semplificare espressioni con
operazioni e potenze di monomi
 Calcolare il M.C.D. e il m.c.m. fra
monomi
 Risolvere problemi con i monomi
 Riconoscere un polinomio e stabilirne
il grado
 Eseguire addizione, sottrazione e
moltiplicazione di polinomi
 Applicare i prodotti notevoli
 Calcolare potenze di binomi
 Risolvere problemi con i polinomi
Equazioni lineari
Trimestre
Enti geometrici fondamentali
Trimestre
Triangoli
Trimestre
Disequazioni lineari
Pentamestre
Funzioni numeriche
Pentamestre
Divisione tra polinomi e scomposizione in
fattori
Pentamestre
 Stabilire se un’uguaglianza è
un’identità
 Stabilire se un valore è soluzione di
un’equazione
 Applicare i principi di equivalenza
delle equazioni
 Risolvere equazioni numeriche intere
 Utilizzare le equazioni per risolvere
problemi
 Identificare le parti del piano e le
figure geometriche principali
 Riconoscere figure congruenti
 Eseguire operazioni tra segmenti e
angoli
 Eseguire costruzioni
 Dimostrare teoremi su segmenti e
angoli
 Riconoscere gli elementi di un
triangolo e le relazioni tra di essi
 Applicare i criteri di congruenza dei
triangoli
 Utilizzare le proprietà dei triangoli
isosceli ed equilateri
 Dimostrare teoremi sui triangoli
 Applicare i principi di equivalenza
delle disequazioni
 Risolvere disequazioni lineari
numeriche e rappresentarne le
soluzioni su una retta
 Risolvere sistemi di disequazioni
 Utilizzare le disequazioni per
risolvere problemi
 Ricercare il dominio naturale e gli
zeri di una funzione numerica
 Riconoscere una funzione di
proporzionalità diretta, inversa,
quadratica e cubica e disegnarne il
grafico
 Riconoscere una funzione lineare e
disegnarne il grafico
 Risolvere problemi utilizzando diversi
tipi di funzioni numeriche
 Eseguire la divisione tra due polinomi
 Applicare la regola di Ruffini
 Raccogliere a fattore comune
 Scomporre in fattori particolari
trinomi di secondo grado
 Utilizzare i prodotti notevoli per
scomporre in fattori un polinomio
 Applicare il teorema del resto e il
teorema di Ruffini per scomporre in
fattori un polinomio
 Calcolare il M.C.D. e il m.c.m. fra
polinomi
Frazioni algebriche
Pentamestre
Equazioni fratte e letterali
Pentamestre
Disequazioni fratte e letterali
Pentamestre
Statistica
Pentamestre
Rette perpendicolari e parallele
Pentamestre
Parallelogrammi e trapezi
Pentamestre
 Determinare le condizioni di esistenza
di una frazione algebrica
 Semplificare frazioni algebriche
 Eseguire operazioni e potenze con le
frazioni algebriche
 Semplificare espressioni con le
frazioni algebriche
 Risolvere equazioni numeriche fratte
 Risolvere equazioni letterali intere e
fratte
 Utilizzare le equazioni per risolvere
problemi
 Risolvere disequazioni numeriche
fratte
 Risolvere disequazioni letterali intere
e fratte
 Raccogliere, organizzare e
rappresentare i dati
 Determinare frequenze assolute e
relative
 Trasformare una frequenza relativa in
percentuale
 Rappresentare graficamente una
tabella di frequenze
 Calcolare gli indici di posizione
centrale di una serie di dati
 Calcolare gli indici di variabilità di
una serie di dati
 Utilizzare la distribuzione normale
per stimare l’incertezza di una
statistica
 Eseguire dimostrazioni e costruzioni
su rette perpendicolari, proiezioni
ortogonali e asse di un segmento
 Applicare il teorema delle rette
parallele e il suo inverso
 Dimostrare teoremi sulle proprietà
degli angoli dei poligoni
 Applicare i criteri di congruenza dei
triangoli rettangoli
 Dimostrare teoremi sui
parallelogrammi e le loro proprietà
 Applicare le proprietà di quadrilateri
particolari: rettangolo, rombo,
quadrato
 Dimostrare teoremi sui trapezi e
utilizzare le proprietà del trapezio
isoscele
 Dimostrare e applicare il teorema di
Talete dei segmenti congruenti
ARTICOLAZIONE TEMPORALE DI MASSIMA DEI CONTENUTI PER LE CLASSI
SECONDE DEL LICEO SCIENTIFICO
Periodo
Conoscenze
Risoluzione ed interpretazione di sistemi
lineari di equazioni
Algebra lineare: matrici, determinanti
Trimestre
Radicali: Operare con espressioni
irrazionali in R
Abilità
 Riconoscere sistemi determinati,
impossibili, indeterminati
 Risolvere un sistema con il metodo di
sostituzione
 Risolvere un sistema con il metodo
del confronto
 Risolvere un sistema con il metodo di
riduzione
 Risolvere un sistema con il metodo di
Cramer
 Risolvere e discutere sistemi letterali
 Risolvere sistemi numerici fratti
 Risolvere sistemi di tre equazioni in
tre incognite
 Risolvere problemi mediante i sistemi
 Riconoscere le matrici e svolgere
semplici operazioni con esse
 Calcolare il determinante di matrici
2x2 e 3x3
 Rappresentare e confrontare tra loro
numeri reali, anche con l’uso di
approssimazioni
 Applicare la definizione di radice
ennesima
 Determinare le condizioni di esistenza
di un radicale
 Semplificare, ridurre allo stesso
indice e confrontare tra loro radicali
numerici e letterali.
 Eseguire operazioni con i radicali
 Trasportare un fattore fuori o dentro il
segno di radice
 Semplificare espressioni con i radicali
 Razionalizzare il denominatore di una
frazione
 Risolvere equazioni, disequazioni e
sistemi di equazioni a coefficienti
irrazionali
 Eseguire calcoli con potenze a
esponente razionale
Il metodo delle coordinate:
il piano cartesiano e la retta
Trimestre
Circonferenze
Trimestre
Circonferenze e poligoni
Trimestre
 Passare dalla rappresentazione di un
punto nel piano cartesiano alle sue
coordinate e viceversa
 Calcolare la distanza tra due punti
 Determinare il punto medio di un
segmento
 Passare dal grafico di una retta alla
sua equazione e viceversa
 Determinare il coefficiente angolare
di una retta
 Scrivere l’equazione di una retta dati
alcuni elementi
 Stabilire se due rette sono incidenti,
parallele o perpendicolari
 Operare con i fasci di rette propri e
impropri
 Risolvere problemi su rette e
segmenti
 Rappresentare l’andamento di un
fenomeno in un grafico cartesiano con
rette e segmenti
 Eseguire costruzioni e dimostrazioni
relative a luoghi geometrici
 Determinare l’equazione di un luogo
geometrico nel piano cartesiano
 Riconoscere le parti della
circonferenza e del cerchio
 Applicare i teoremi sulle corde
 Riconoscere le posizioni reciproche di
retta e circonferenza, ed eseguire
costruzioni e dimostrazioni
 Riconoscere le posizioni reciproche di
due circonferenze, ed eseguire
dimostrazioni
 Applicare il teorema delle rette
tangenti a una circonferenza da un
punto esterno
 Applicare le proprietà degli angoli al
centro e alla circonferenza
corrispondenti
 Risolvere problemi relativi alla
circonferenza e alle sue parti
 Riconoscere poligoni inscritti e
circoscritti e applicarne le proprietà
 Applicare le proprietà dei punti
notevoli di un triangolo
 Applicare teoremi su quadrilateri
inscritti e circoscritti
 Applicare teoremi su poligoni regolari
e circonferenza
 Risolvere problemi relativi a poligoni
inscritti e circoscritti
Equazioni di secondo grado
Pentamestre
Parabole, equazioni e sistemi
Pentamestre
Disequazioni di II grado
Pentamestre
 Applicare la formula risolutiva delle
equazioni di secondo grado
 Risolvere equazioni numeriche di
secondo grado
 Risolvere e discutere equazioni
letterali di secondo grado
 Calcolare la somma e il prodotto delle
radici di un’equazione di secondo
grado senza risolverla
 Scomporre trinomi di secondo grado
 Risolvere quesiti riguardanti
equazioni parametriche di secondo
grado
 Risolvere problemi di secondo grado
 Disegnare una parabola, individuando
vertice e asse
 Interpretare graficamente le equazioni
di secondo grado
 Determinare l’equazione di una
parabola, noti alcuni elementi
 Risolvere problemi di massimo e
minimo mediante le parabole
 Risolvere algebricamente e
interpretare graficamente sistemi di
secondo grado
 Risolvere e interpretare graficamente
disequazioni lineari
 Studiare il segno di un prodotto
 Studiare il segno di un trinomio di
secondo grado
 Risolvere disequazioni di secondo
grado intere e fratte e rappresentarne
le soluzioni
 Interpretare graficamente
disequazioni di secondo grado
Equazioni e disequazioni di grado
superiore
Pentamestre
Applicazioni delle disequazioni
Pentamestre
Probabilità
Pentamestre
 Risolvere equazioni binomie, trinomie
e biquadratiche
 Risolvere equazioni di grado
superiore al secondo con la
scomposizione in fattori
 Risolvere algebricamente e
interpretare graficamente particolari
sistemi di grado superiore al secondo
 Risolvere particolari sistemi
simmetrici di grado superiore al
secondo e sistemi omogenei
 Risolvere problemi utilizzando
sistemi di secondo grado
 Risolvere disequazioni di grado
superiore al secondo
 Risolvere disequazioni fratte
 Risolvere sistemi di disequazioni in
cui compaiono disequazioni di
secondo grado o di grado superiore
 Utilizzare le disequazioni di secondo
grado per risolvere problemi
 Risolvere quesiti riguardanti
equazioni e disequazioni parametriche
 Applicare le disequazioni per
determinare il dominio e studiare il
segno di funzioni
 Applicare le disequazioni per
risolvere equazioni irrazionali
 Applicare le disequazioni per
risolvere disequazioni irrazionali
 Applicare le disequazioni per
risolvere equazioni con i valori
assoluti
 Applicare le disequazioni per
risolvere disequazioni con i valori
assoluti
 Riconoscere se un evento è aleatorio,
certo o impossibile
 Determinare la probabilità di un
evento secondo la definizione classica
 Determinare la probabilità di un
evento aleatorio, secondo la
definizione statistica
 Determinare la probabilità di un
evento aleatorio, secondo la
definizione soggettiva
 Calcolare la probabilità della somma
logica di eventi
 Calcolare la probabilità del prodotto
logico di eventi dipendenti e
indipendenti
 Calcolare la probabilità condizionata
 Descrivere esperimenti aleatori
mediante variabili aleatorie, tabelle di
frequenza e diagrammi
Superfici equivalenti e aree
Pentamestre
Teoremi di Euclide e di Pitagora
Pentamestre
Proporzionalità e similitudine
Pentamestre
 Applicare le proprietà
dell’equivalenza tra superfici
 Riconoscere superfici equivalenti
 Applicare i teoremi sull’equivalenza
fra parallelogrammi, fra triangolo e
parallelogramma, fra trapezio e
triangolo, fra poligono circoscritto e
triangolo
 Costruire poligoni equivalenti
 Calcolare le aree di poligoni notevoli:
rettangolo, quadrato,
parallelogramma, triangolo, trapezio,
poligono con diagonali
perpendicolari, poligono circoscritto
 Risolvere problemi di algebra
applicata alla geometria
 Applicare il primo teorema di Euclide
 Applicare il teorema di Pitagora
 Applicare il secondo teorema di
Euclide
 Utilizzare le relazioni sui triangoli
rettangoli con angoli di 30°, 45°, 60°
 Risolvere problemi mediante i
teoremi di Euclide e di Pitagora
 Determinare la misura di una
grandezza
 Riconoscere grandezze direttamente
proporzionali
 Eseguire dimostrazioni applicando il
teorema di Talete e il teorema della
bisettrice
 Applicare i tre criteri di similitudine
dei triangoli
 Applicare le relazioni di
proporzionalità che esprimono i
teoremi di Euclide
 Applicare teoremi relativi alla
similitudine tra poligoni e tra poligoni
regolari
 Applicare i teoremi relativi alla
similitudine nella circonferenza
 Applicare le proprietà della sezione
aurea di un segmento
 Calcolare aree e perimetri di triangoli
e poligoni simili
 Calcolare la misura della lunghezza di
una circonferenza e dell’dell’area di
un cerchio
 Applicare le proprietà della misura e
delle proporzioni tra grandezze per
risolvere problemi geometrici
 Risolvere problemi relativi a figure
simili
 Risolvere problemi relativi a
lunghezza della circonferenza e area
del cerchio
Trasformazioni geometriche
Pentamestre
 Applicare trasformazioni geometriche
a punti e figure
 Riconoscere i punti uniti e le figure
unite in una trasformazione
 Comporre trasformazioni
 Riconoscere le isometrie: traslazione,
rotazione, simmetria assiale e
simmetria centrale
 Riconoscere le simmetrie delle figure
 Comporre isometrie
 Applicare le proprietà dell’omotetia
 Riconoscere le equazioni di
particolari isometrie nel piano
cartesiano
 Riconoscere le equazioni di
un’omotetia nel piano cartesiano
 Nel piano cartesiano, applicare
isometrie e omotetie a punti e rette,
determinando coordinate ed equazioni
degli elementi trasformati
 Determinare le equazioni di
trasformazioni composte
ARTICOLAZIONE TEMPORALE DI MASSIMA DEI CONTENUTI PER LE CLASSI
TERZE DEL LICEO SCIENTIFICO
Periodo
Conoscenze
Ripasso di equazioni e disequazioni
Funzioni e loro rappresentazione grafica
Trasformazioni geometriche
Abilità




Primi elementi di geometria analitica
(ripasso)


Retta e fasci di rette
Luoghi geometrici
Saper risolvere equazioni e
disequazioni in modulo e irrazionali
Saper riconoscere le proprietà di una
funzione
Operare con le funzioni
Saper calcolare dominio, segno e zeri
di funzioni algebriche intere/fratte,
razionali/irrazionali
Saper classificare le trasformazioni
geometriche, conoscere le relative
equazioni e saperle applicare
Costruire grafici deducibili
Saper determinare: coordinate di
punti, distanze fra punti, punto
medio di un segmento e baricentro
di un triangolo, equazione di rette e
relativa rappresentazione

Saper rappresentare la retta in un
piano cartesiano, saperne
determinare l’equazione in
relazione ad assegnate condizioni.
Saper risolvere problemi di
geometria analitica sulla retta

Saper riconoscere, classificare e
rappresentare i fasci di rette
Saper rappresentare: semipiani,
segmenti, semirette, angoli, strisce
e poligoni
Saper risolvere graficamente
equazioni e disequazioni lineari in
due variabili
Saper definire e determinare
l’equazione di un luogo geometrico
Saper impostare e risolvere
problemi riguardanti la parabola
Saper impostare e risolvere
problemi riguardanti li fasci di
parabole (cenni)
Trimestre
La parabola





Circonferenza

Ellisse

Iperbole

Coniche in generale
Pentamestre
Funzioni deducibili
dalle coniche
Problemi geometrici
Funzioni logaritmiche ed esponenziali



Logaritmi e relative proprietà

Pentamestre
Equazioni e disequazioni logaritmiche ed
esponenziali
Modelli di crescita e decadimento


Elementi di statistica descrittiva
Rappresentazioni grafiche
Pentamestre
Indicatori statistici.
Dipendenza statistica




Rappresentare nel piano cartesiano
una conica di data equazione e
conoscere il significato dei
parametri della sua equazione
Scrivere l’equazione di una conica
date alcune condizioni
Saper impostare e risolvere
problemi riguardanti le coniche e le
rette
Saper riconoscere dall’equazione
irrazionale un ramo di conica e
saper utilizzare ciò per la
risoluzione grafica di equazioni e
disequazioni
Saper analizzare un problema
geometrico individuando proprietà,
teoremi e relazioni coinvolte e
scegliendo opportunamente le
incognite; saper risolvere con
metodi grafici sistemi parametrici
misti (cenni)
Semplificare espressioni contenenti
esponenziali e logaritmi applicando
in particolare le proprietà dei
logaritmi
Saper costruire ed interpretare il
grafico di una funzione logaritmica
e di una esponenziale; saper
costruire grafici deducibili
Saper risolvere equazioni
esponenziali e logaritmiche
Saper costruire modelli di crescita o
decrescita esponenziale e
logaritmica
Saper costruire tabelle di variabili
statistiche e interpretarne i risultati
Calcolare valori medi e misure di
varibilità di una distribuzione
Saper rappresentare graficamente i
valori di una distribuzione
Saper analizzare distribuzioni
statistiche e riconoscere se esiste
dipendenza statistica (correlazione
e regressione).
ARTICOLAZIONE TEMPORALE DI MASSIMA DEI CONTENUTI PER LE CLASSI
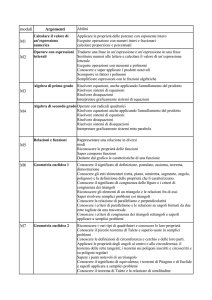
QUARTE DEL LICEO SCIENTIFICO
Periodo
Conoscenze
Funzioni, equazioni e disequazioni
goniometriche.
Trimestre
Trigonometria
Numeri complessi
Abilità

Saper calcolare le funzioni
goniometriche di un angolo e,
viceversa, risalire all’angolo
data una sua funzione
goniometrica.

Saper semplificare espressioni
contenenti funzioni
goniometriche, anche
utilizzando opportunamente le
formule di addizione,
sottrazione, duplicazione e
bisezione.

Tracciare il grafico di funzioni
goniometriche anche mediante
l’utilizzo di opportune
trasformazioni geometriche.

Risolvere equazioni e
disequazioni goniometriche.

Saper costruire e analizzare
modelli di andamenti periodici
nella descrizione di fenomeni
fisici o di altra natura.
Risolvere un triangolo
rettangolo.


Applicare i teoremi sui triangoli
rettangoli per determinare
lunghezze di segmenti e
ampiezze di angoli.

Conoscere il Teorema della
corda e le sue applicazioni.

Risolvere un triangolo
qualsiasi.

Applicare i teoremi sui triangoli
qualunque per determinare
lunghezze di segmenti e
ampiezze di angoli.

Eseguire operazioni tra numeri
complessi
Utilizzare le tecniche e le
procedure del calcolo algebrico
nel campo dei numeri
complessi, rappresentandole
anche sotto forma grafica.
Risolvere semplici equazioni in
C.
Classificare un’affinità e
individuarne le proprietà
invarianti.


Pentamestre
Trasformazioni geometriche


Individuare le equazioni della
rotazione

Applicare le trasformazioni
geometriche alle coniche
(cenni).

Saper costruire grafici
deducibili
Successioni e progressioni aritmetiche
e geometriche
Funzioni, equazioni e disequazioni
esponenziali e logaritmiche
Pentamestre
Calcolo combinatorio.
Calcolo delle probabilità

Rappresentare i termini di una
successione e saperne stabilire
il comportamento. Conoscere
definizioni e proprietà di una
progressione aritmetica o
geometrica.

Semplificare espressioni
contenenti esponenziali e
logaritmi, applicando in
particolare le proprietà dei
logaritmi.

Risolvere semplici equazioni e
disequazioni esponenziali e
logaritmiche.

Tracciare il grafico di funzioni
esponenziali e logaritmiche
mediante anche l’utilizzo di
opportune trasformazioni
geometriche.

Saper costruire modelli di
crescita o decrescita
esponenziale o logaritmica

Saper calcolare permutazioni,
disposizioni e combinazioni,
semplici o con ripetizioni.

Calcolare la probabilità di un
evento secondo la definizione
classica, anche utilizzando le
regole del calcolo
combinatorio.

Calcolare la probabilità
dell’evento contrario e
dell’evento unione e
intersezione di due eventi dati.

Stabilire se due eventi sono
incompatibili o indipendenti.

Utilizzare il teorema delle
probabilità composte, il
teorema delle probabilità totali
e il teorema di Bayes.

Cenni all’utilizzo di modelli
probabilistici per risolvere
problemi ed effettuare scelte
consapevoli.
Geometria euclidea dello spazio
Geometria analitica nello spazio

Riconoscere nello spazio la
posizione reciproca di due
rette, di due piani o di una retta
e un piano.

Conoscere i solidi principali e le
relative proprietà.

Conoscere le formule e le
strategie per calcolare
l’estensione dei solidi.

Scrivere l’equazione di una
retta o di un piano nello spazio,
soddisfacente condizioni date
(in particolare di parallelismo e
perpendicolarità).

Determinare la distanza di un
punto da un piano o da una
retta nello spazio riferito a un
sistema di riferimento
cartesiano.

Scrivere l’equazione di una
superficie sferica.
Pentamestre
Strumenti di verifica:
Interrogazioni ed interventi
Esercizi – test – questionari
Problemi
Relazioni
Prove strutturate e semistrutturate
Criteri di valutazione:
ARTICOLAZIONE TEMPORALE DI MASSIMA DEI CONTENUTI PER LE CLASSI
QUINTE DEL LICEO SCIENTIFICO
Periodo
Conoscenze
Abilità
Ripasso e approfondimenti ( o da svolgere se
non fatti negli anni precedenti):

funzioni reali di variabile reale

Funzioni inverse, funzioni composte,
grafici deducibili

Elementi di calcolo combinatorio e
probabilità
 saper
determinare
dominio
e
codominio
 saper determinare le principali
caratteristiche di funzione (dominio,
parità,
segno,
periodicità,
intersezioni assi)
 saper
determinare
la
funzione
composta e ricavarne le principali
caratteristiche grafiche
 saper determinare la funzione inversa e
ricavarne le principali caratteristiche
grafiche
 saper ricavare le funzioni inverse delle
funzioni circolari e saper disegnare i
relativi grafici
 saper rappresentare grafici deducibili
da grafici conosciuti

Saper
calcolare
permutazioni,
disposizioni
e
combinazioni,
semplici o con ripetizioni.

Calcolare la probabilità di un evento
secondo la definizione classica,
anche utilizzando le regole del
calcolo combinatorio.

Calcolare la probabilità dell’evento
contrario e dell’evento unione e
intersezione di due eventi dati.

Stabilire se due eventi
incompatibili o indipendenti.

Utilizzare
il
teorema
delle
probabilità composte, il teorema
delle probabilità totali e il teorema di
Bayes.

Cenni all’utilizzo di modelli
probabilistici per risolvere problemi
ed effettuare scelte consapevoli.

Riconoscere
nello
spazio
la
posizione reciproca di due rette, di
due piani o di una retta e un piano.

Conoscere i solidi principali e le
relative proprietà.

Conoscere le formule e le strategie
per calcolare l’estensione dei solidi.

Scrivere l’equazione di una retta o di
un piano nello spazio, soddisfacente
condizioni date (in particolare di
Trimestre

Geometria nello spazio
sono
parallelismo e perpendicolarità).

Determinare la distanza di un punto
da un piano o da una retta nello
spazio riferito a un sistema di
riferimento cartesiano.

Scrivere
l’equazione
di
una
superficie sferica.
Conoscere i solidi principali e le
relative proprietà.

LIMITI

Limiti di successioni e definizione del
numero e

Limiti delle funzioni

Teoremi fondamentali sui limiti

Infiniti, infinitesimi e forme indeterminate

Asintoti verticali, orizzontali ed obliqui

Problemi con i limiti
FUNZIONI CONTINUE
 Funzioni continue e punti di discontinuità

Conoscere le formule e le strategie
per calcolare l’estensione dei
solidi.

saper verificare un limite

saper applicare i teoremi sui limiti

saper calcolare i limiti e saper
risolvere i limiti di forme
indeterminate

saper calcolare i limiti applicando
anche i limiti notevoli

saper applicare il calcolo dei limiti
nella risoluzione di problemi

saper caratterizzare
discontinuità

saper prolungare per continuità una
funzione in punti di discontinuità
eliminabile

saper applicare i teoremi delle
funzioni continue

Saper riconoscere la convergenza e
divergenza di una serie

Saper
definire
il
rapporto
incrementale e saper conoscere il
concetto di derivata

Sapere il significato geometrico di
derivata
 Teoremi sulle funzioni continue
SERIE

Definizione di serie numerica

Serie
convergenti,
indeterminate
i
punti
di
divergenti,
DERIVATE

Funzioni derivate e primitive: teoremi
relativi

Calcolo delle derivate

definizione di derivata di una funzione e
suo significato geometrico

saper calcolare la funzione derivata e
le derivate successive

derivate delle funzioni elementari


regole di derivazione, derivata di una
funzione composta
saper determinare continuità
derivabilità di una funzione

saper applicare
derivazione

saper studiare la crescenza o la
decrescenza di una funzione e
trovare i punti di massimo, minimo e
flesso

saper caratterizzare i punti di non

derivata della funzione inversa

equazione della retta tangente in un punto
al grafico di una funzione

continuità e derivabilità

derivate di ordine superiore
le
regole
e
di

Pentamestre
teoremi
fondamentali
differenziale
del

differenziale di una funzione

significato fisico della derivata.
derivabilità
calcolo

risolvere problemi con applicazione
delle derivate alla fisica

saper applicare i teoremi sul calcolo
differenziale

saper risolvere i limiti applicando il
teorema di De l’Hospital
TEOREMI DEL CALCOLO
DIFFERENZIALE
 teorema di Rolle,
 teorema di Lagrange e sue conseguenze
 teorema di Cauchy
 teorema di De L’Hospital
STUDIO DI FUNZIONI



Studio completo di funzione
Risoluzione di problemi di max o min
La
risoluzione
approssimata
un’equazione
 saper calcolare i massimi e i minimi
assoluti di una funzione
di
 saper studiare il grafico di una funzione
razionale
 saper studiare il grafico di una funzione
irrazionale
 saper studiare il grafico di una funzione
trascendente

saper ricavare il grafico di f dal grafico
di f’ e viceversa

Saper impostare e risolvere problemi
di massimo e minimo
saper
applicare
i
metodi
di
approssimazione di aree

INTEGRALI

Integrali indefiniti: definizione e calcolo di
integrali immediati
 saper calcolare integrali indefiniti
immediati

Calcolo di integrali indefiniti
 saper integrare le funzioni razionali

Integrale definito

Proprietà e teorema della media
 saper integrare per parti e per semplici
sostituzioni

Aree e volumi
 saper lavorare con le funzioni primitive
di una funzione data

lunghezza di un arco di curva
 saper calcolare integrali definiti

area di una superficie di rotazione

integrali impropri
 saper applicare le proprietà degli integrali
definiti

Integrazione numerica
 saper applicare il teorema della media
 saper calcolare le aree di domini piani
 saper risolvere integrali impropri
 saper calcolare volumi di solidi di
rotazione
 saper calcolare la lunghezza di un arco di
curva
 saper calcolare l’area di una superficie di
rotazione
 saper operare con la funzione integrale:
teorema di Torricelli-Barrow

saper
applicare
i
metodi
approssimazione di aree
di
EQUAZIONI DIFFERENZIALI

equazioni differenziali del primo ordine

equazioni differenziali del tipo y’ = f(x)

equazioni differenziali a variabili separabili

equazioni differenziali lineari del primo
ordine

equazioni differenziali del secondo ordine

saper riconoscere e risolvere
un’equazione differenziale
DISTRIBUZIONI DI PROBABILITA’

le variabili casuali discrete e le distribuzioni
di probabilità

i valori caratterizzanti una variabile casuale
discreta

le distribuzioni di probabilità di uso
frequente

le variabili casuali standardizzate

le variabili casuali continue
Strumenti di verifica:
Interrogazioni ed interventi
Esercizi – test – questionari
Problemi
Relazioni
Prove strutturate e semistrutturate
Criteri di valutazione:

Saper riconoscere le principali
distribuzioni di probabilità nel discreto
e nel continuo

Saper individuare la distribuzione
normale come ’limite’ di una
distribuzione
binomiale:
standardizzazione
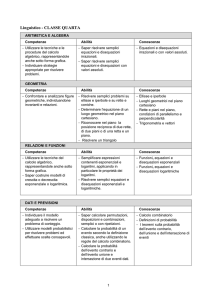
VALUTAZIONE SCRITTO PRIMO BIENNIO
10 - 9
8
7
6
Ha una conoscenza
piena e completa dei
contenuti, arricchita da
approfondimenti
personali
Ha una conoscenza
articolata e completa
dei contenuti
disciplinari
Ha una conoscenza
discreta, ed
abbastanza articolata
dei contenuti
disciplinari
Conosce e comprende i
contenuti essenziali
E’ autonomo nella
soluzione dei problemi
e nella utilizzazione
delle sue conoscenze
anche in contesti
interdisciplinari
Collega
autonomamente i
contenuti fra loro ed
li applica a diversi
contesti
Sa applicare i
contenuti a diversi
contesti con parziale
autonomia
Riesce a compiere
semplici applicazioni dei
contenuti acquisiti
5
4-3
LIVELLI /
DESCRITTORI
CONOSCENZE
COMPETENZE
Ha appreso i
contenuti in maniera
superficiale, li
distingue e collega fra
loro in modo
frammentario
Richiede di essere
continuamente
guidato nella
applicazione dei
contenuti
Non ha conoscenze o ha
una conoscenza
frammentaria e non
corretta dei contenuti
Non riesce ad applicare
le procedure necessarie al
compito a causa della
frammentarietà delle
conoscenze
VALUTAZIONE SCRITTO SECONDO BIENNIO
10 - 9
8
7
6
Ha una conoscenza
piena e completa dei
contenuti, arricchita da
approfondimenti
personali
Ha una conoscenza
articolata e completa
dei contenuti
disciplinari
Ha una conoscenza
discreta, ed
abbastanza articolata
dei contenuti
disciplinari
Conosce e comprende i
contenuti essenziali
E’ autonomo nella
soluzione dei problemi
e nella utilizzazione
delle sue conoscenze
anche in contesti
interdisciplinari
Collega
autonomamente i
contenuti fra loro ed
li applica a diversi
contesti
Sa applicare i
contenuti a diversi
contesti con parziale
autonomia
Riesce a compiere
semplici applicazioni dei
contenuti acquisiti
5
4-3
LIVELLI /
DESCRITTORI
CONOSCENZE
COMPETENZE
Ha appreso i
contenuti in maniera
superficiale, li
distingue e collega fra
loro in modo
frammentario
Richiede di essere
continuamente
guidato nella
applicazione dei
contenuti
Non ha conoscenze o ha
una conoscenza
frammentaria e non
corretta dei contenuti
Non riesce ad applicare
le procedure necessarie al
compito a causa della
frammentarietà delle
conoscenze
VALUTAZIONE SCRITTO QUINTO ANNO SI FA RIFERIMENTO ALLE GRIGLIE DEL MIUR
VALUTAZIONE DEL COLLOQUIO
DESCRITTORI
Possesso dei nuclei
concettuali
fondamentali
dell’argomento
10 / 9
Esauriente, rigoroso e
argomentato
8/7
Corretto e completo
DESCRITTORI DI LIVELLO
6
5
Limitato ai contenuti essenziali
Lacunoso e solo
parzialmente corretto
La comprensione è puntuale, Individua i concetti chiave Coglie correttamente i concetti
Coglie in modo parziale
con note personali di analisi e le informazioni
chiave, ma possiede in modo
e/o non del tutto corretto
Strutturazione ed
e sintesi; costruisce
necessarie per operare
superficiale ed incerto le categorie le informazioni chiave.
elaborazione delle
collegamenti corretti ed
analisi esaurienti.
di analisi. Non sempre è in grado Stabilisce, solo se
conoscenze
efficaci anche tra ambiti
Costruisce collegamenti e di compiere sintesi
guidato, connessioni
culturali diversi
nessi corretti ma semplici autonomamente.
elementari
Articola la comunicazione in Articola la comunicazione Articola la comunicazione in
Adotta un linguaggio
Padronanza delle
modo efficace ed adeguato
in modo semplice; adotta
modo poco coerente. Si esprime
impreciso; riconosce i
strutture
con un lessico elementare, non
registri specifici, ma non
linguistiche ed uso allo scopo, alla situazione ed un linguaggio corretto e
all’interlocutore; usa con
preciso, ma non sempre
sempre preciso; comprende i
è in grado di usarli.
del registro
evidenziando un possesso registri specifici, ma non è sempre Possiede strutture
specifico adeguato proprietà il registro
pertinente
sicuro dei registri specifici in grado di usarli
linguistiche elementari
alla trattazione
PER OGNI DESCRITTORE VIENE ATTRIBUITO UN VOTO DA 1 A 10; IL VOTO FINALE E' LA MEDIA DEI VOTI ATTRIBUITI.
4/3
Gravemente lacunoso e/o
errato
Non riconosce le informazioni
chiave; non è in grado di
stabilire nessi e collegamenti
logici
Articola il discorso in modo
incoerente e inefficace; usa
strutture linguisticocomunicative improprie e/o
scorrette; non riconosce né usa
registri specifici
MAPPA DI LIVELLI DI VALUTAZIONE
LIVELLI
Insuff. Grave
(voto: fino a 4)
Insuff. lieve
CONOSCENZA
COMPRENSIONE
Nessuna o
lacunosa
Parziale
Nessuna o scarsa
Non corretta
Confusa
Completa, ma
non approfondita
Completa
(voto:6)
Discreto
Completa e
organica
Articolata e
approfondita
USO EGISTRO
SPECIFICO
PARTECIPAZIONE
METODO DI
STUDIO
IMPEGNO
Di disturbo o passiva
Disorganizzato
Scarso
Passiva
Ripetitivo
Discontinuo
Complessiva, ma
imprecisa
Completa
Non sempre
corretta
Corretta ma
meccanica
Corretta
Confuso,
frammentario
Non sempre
corretto
Sufficientemente
corretto
Corretto
Sollecitata
Accettabile
Diligente
Sollecitata
Produttivo
Costante
Completa
Corretta
Corretto e preciso
Attiva
Organico
Costante
Completa e
approfondita
Personale
Appropriato ed
efficace
Propositiva
Elaborativo ed
autonomo
Costante ed
autonomo
(voto: 5)
Sufficiente
APPLICAZIONE
(voto:7)
Buono
(voto: 8)
Ottimo
(voto: 9/10)