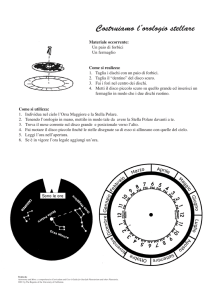
Esercizio 1
Due dischi di ferro coassiali, di raggi r1 = 0.1 m e r2 = 0.2 m e masse m1 = 2 Kg e
m2 = 3 Kg, sono saldati insieme e possono ruotare senza attrito attorno ad un asse verticale
passante per il centro di massa. Sul disco r1 e’ avvolto un filo a cui e’ appesa una massa
m = 1 Kg. All’istante t=0 la massa m, inizialmente ferma, viene lasciata cadere.
a) Calcolare il tempo t0 necessario affiche’ la massa m percorra una distanza h = 10 m.
b) Sul bordo del disco r2 e’ fissato un magnetino di massa m0 = 10g e dimensioni
trascurabili. La forza magnetica che lo tiene attaccato al disco vale F = 1.5 N. Dire se al
tempo t0 il magnetino e’ ancora attaccato al disco.
Soluzione
Calcoliamo il momento d’inerzia del sistema dei due dischi.
1
1
I = I1 + I2 = m1 r12 + m2 r22 = 0.5(2 · 0.01 + 3 · 0.04) = 0.07Kg m2
2
2
Applichiamo la II legge di Newton al corpo di massa m.
mg − T = ma
(1)
(2)
Applichiamo la II equazione cardinale al sistema dei due dischi.
T r1 = Iα
(3)
Poiche’ a = αr1 possiamo scrivere la (2) come:
mg − T = mαr1
(4)
Moltiplicando ambo i membri per r1 :
mgr1 − T r1 = mαr12
(5)
mgr1 = α(I + mr12 )
(6)
Sommando la (3) e la (5):
Da questa ricaviamo α
mgr1
1 · 9.8 · 0.1
0.98
=
=
= 12.24 rad/sec2
2
I + mr1
0.07 + 1 · 0.01
0.08
L’accelerazione lineare si ottiene da:
α=
a = αr1 = 12.24 · 0.1 = 1.224 m/sec2
(7)
(8)
Il moto della massa m e’ uniformemente accelerato, quindi:
1
h = at20
2
1
(9)
e quindi
s
s
2h
20
=
= 4.04 sec
t0 =
a
1.224
Al tempo t0 la velocita’ angolare dei dischi e’
ω = αt0 = 14 · 4.04 = 56.6 rad/sec
(10)
(11)
La forza centrifuga che agisce sul magnetino e’:
f = m0 ω 2 r2 = 0.01 · 56.62 · 0.2 = 6.4 N
che e’ piu’ grande della forza magnetica per cui il magnetino si sara’ staccato.
2
(12)