Argomento 1_Progettazione sismica

DIPARTIMENTO DI INGEGNERIA MECCANICA E STRUTTURALE
Corso di Aggiornamento su Problematiche Strutturali
Collegio dell’
dell ’Ordine dei Geometri - Verona
Progettazione Sismica delle Strutture
Aspetti generali e normativa sismica italiana (O.P.C.M. 3274)
Docente:
Ing. Fabio Ferrario
Dicembre 2005
1
La progettazione sismica delle strutture
Azioni statiche
Stato limite ultimo
Stato limite di esercizio
Le vecchie normative sismiche, di solito, non prevedevano la verifica a più livelli.
Le lezioni degli ultimi terremoti hanno insegnato come le strutture progettate con le vecchie
normative spesso raggiungono solo l’ultimo scopo – la prevenzione del collasso – ma non
sono in grado di evitare i danni su elementi strutturali e non.
d
Un approccio progettuale ottimale deve prevedere adeguate prestazioni strutturali per
ciascun livello di intensità dell’azione sismica.
Azione sismica
La struttura deve
resistere:
ad azioni di piccola entità senza danneggiarsi
ad azioni di moderata entità subendo danni “riparabili”
ad azioni di elevata entità senza raggiungere il collasso
2
1
La progettazione sismica delle strutture
Un approccio progettuale esauriente deve prevedere i seguenti pa ssi:
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
[Rif. Bibl. Gioncu V., Mazzolani F.M., 2002. Ductility od
seismic resistant steel structures. Spon Press, New York]
3
La progettazione sismica delle strutture
Un approccio progettuale esauriente deve prevedere i seguenti pa ssi:
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
[Rif. Bibl. Gioncu V., Mazzolani F.M., 2002. Ductility od
seismic resistant steel structures. Spon Press, New York]
4
2
Selezione dei livelli di prestazione richiesti
In generale è ragionevole supporre che le strutture debbano sopportare
eventi di moderata intensità senza subire danni, mentre per eventi rari, di
elevata intensità, è possibile tollerare un eventuale danneggiamento purché
sia garantita la stabilità globale dell’edificio.
Fanno eccezione edifici di carattere particolare per l’utilizzo o la
destinazione d’uso:
- costruzioni il cui collasso possa causare da disastri naturali: impianti
nucleari, dighe;
- costruzioni di importanza strategica: ospedali, centri di comunicazione;
- infrastrutture di rilevante importanza: linee di comunicazione, ponti, ecc;
- costruzioni contenenti oggetti di valore unico: musei, ecc.
A parte suddette eccezioni, comunque, occorre definire in via preliminare i
livelli di danno accettabili.
5
Selezione dei livelli di prestazione richiesti
Esistono alcuni criteri generalmente accettati per definire i livelli di
prestazione richiesti.
1) La sicurezza delle vite umane è sicuramente un requisito primario, anche
se la definizione di un livello accettabile di perdite pone gravi problemi etici.
2) La prevenzione del collasso strutturale è strettamente legata con la
sicurezza delle vite umane ed in genere deve essere garantita per terremoti
di elevata intensità.
3) La limitazione dei danni agli edifici: si distingue tra danni strutturali che
non possono essere riparati e danni riparabili. I danni possono riguardare
elementi strutturali e non.
4) La limitazione di interruzioni delle attività produttive: a volte il valore
delle attività connesse all’utilizzo dell’edificio è maggiore rispetto al valore
dell’edificio stesso e la loro interruzione è intollerabile.
5) La limitazione delle perdite relative al patrimonio storico ed
architettonico.
6
3
Selezione dei livelli di prestazione richiesti
Definizione dei livelli di prestazione richiesti in funzione di ciascun stato limite
7
Selezione dei livelli di prestazione richiesti
Per la definizione dei livelli di protezione minimi accettabili occorre quindi
ricercare la soluzione ottima in termini di costi iniziali, perdite e costi di
riparazione associati a ciascun livello di prestazione.
8
4
La progettazione sismica delle strutture
Un approccio progettuale esauriente deve prevedere i seguenti pa ssi:
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
[Rif. Bibl. Gioncu V., Mazzolani F.M., 2002. Ductility od
seismic resistant steel structures. Spon Press, New York]
9
Selezione dei livelli di verifica strutturale
Le strutture possono essere soggette a terremoti di bassa, moderata od
elevata intensità, subendo nessun danno, danni lievi, moderati od elevati o
infine raggiungendo il collasso di una loro porzione o globale.
E’ ovvio che il livello di danno dipende dall’intensità del terremoto:
terremoti di intensità moderata hanno una probabilità di occorrenza più
elevata, i terremoti di intensità moderata sono più rari, mentre terremoti di
elevata intensità possono verificarsi al massimo una o due volte nella vita
della struttura.
Per garantire una risposta strutturale adeguata occorre quindi adottare un
approccio a più livelli definendo alcuni stati limite in funzione della
probabilità di danno di elementi non strutturali o strutturali. Esistono
approcci multi-livello a quattro, tre o due livelli.
10
5
Selezione dei livelli di verifica strutturale
Approccio a quattro livelli
11
Selezione dei livelli di verifica strutturale
Approccio a tre livelli (FEMA - USA)
stato limite di servizio (per terremoti frequenti): gli elementi strutturali e
non strutturali non devono subire danni;
stato limite di danno (per terremoti occasionali): possono verificarsi danni
negli elementi strutturali e solo un moderato danneggiamento nelle
strutture;
stato limite ultimo (per terremoti rari): possono verificarsi danni ad elementi
strutturali e non, ma la sicurezza delle vite umane deve essere garantita.
Approccio a due livelli (Eurocodici – Europa)
stati limite di esercizio: le strutture devono rimanere in campo elastico o
subire piccole plasticizzazioni; gli elementi non strutturali non devono
subire danni;
stato limite ultimo: le strutture possono sfruttare la loro capacità di
deformarsi oltre il limite elastico; gli elementi non strutturali possono
danneggiarsi.
12
6
Selezione dei livelli di verifica strutturale
Approccio a tre livelli
13
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Requisiti di sicurezza e criteri di verifica
SICUREZZA NEI CONFRONTI DELLA STABILITÀ (STATO LIMITE ULTIMO – S.L.U.)
Sotto l’effetto della azione sismica di progetto, le strutture degli edifici, ivi compresi gli eventuali
dispositivi antisismici di isolamento e/o dissipazione, pur subendo danni di grave entità agli elementi
strutturali e non strutturali, devono mantenere una residua resistenza e rigidezza nei confronti delle
azioni orizzontali e l’intera capacità portante nei confronti dei carichi verticali.
Periodo di ritorno dell’evento sismico di 475 anni
PROTEZIONE NEI CONFRONTI DEL DANNO (STATO LIMITE DI DANNO – S.L.D.)
Le costruzioni nel loro complesso, includendo gli elementi strutturali e quelli non strutturali,
ivi comprese le apparecchiature rilevanti alla funzione dell’edificio, non devono subire danni gravi
ed interruzioni d’uso in conseguenza di eventi sismici che abbiano una probabilità di occorrenza
più elevata di quella della azione sismica di progetto.
Periodo di ritorno dell’evento sismico di 95 anni
N.B: Ogni stato limite viene verificato per una diversa intensità dell’azione sismica.
Periodo di ritorno TR pari a TR = − N
, con ρ n probabilità di superamento (10%) in N anni:
ln(1 − ρn )
S.L.U.: N = 50 anni
S.L.D.: N = 10 anni
14
7
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Requisiti di sicurezza e criteri di verifica
SODDISFACIMENTO DEI REQUISITI GENERALI
Lo stato limite ultimo si considera soddisfatto se vengono seguite le disposizioni contenute nelle
norme, con riferimento particolare a:
- la scelta della azione sismica di progetto in relazione alla zonazione sismica ed alle categorie
di suolo di fondazione;
- l’adozione di un modello meccanico della struttura in grado di descriverne con accuratezza la
risposta sotto azione dinamica;
- la scelta di un metodo di analisi adeguato alle caratteristiche della struttura;
- l’esecuzione con esito positivo delle verifiche di resistenza e di compatibilità degli spostamenti;
- l’adozione di tutte le regole di dettaglio volte ad assicurare caratteristiche di duttilità agli elementi
strutturali ed alla costruzione nel suo insieme, secondo quanto indicato nei capitoli relativi a
strutture realizzate con i diversi materiali.
Lo stato limite di danno si considera soddisfatto se vengono seguite le disposizioni contenute nelle
norme, con particolare riferimento allo spettro di progetto, agli effetti del II ordine ed ai dettagli
costruttivi contenuti nei capitoli relativi a strutture realizzate con i diversi materiali.
15
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Requisiti di sicurezza e criteri di verifica
PRESCRIZIONI RELATIVE AI TERRENI DI FONDAZIONE
Il sito di costruzione ed i terreni in esso presenti dovranno in generale essere esenti da rischi
di instabilità di pendii e di cedimenti permanenti causati da fenomeni di liquefazione o eccessivo
addensamento in caso di terremoto.
L’occorrenza di tali fenomeni dovrà essere indagata e valutata secondo quanto stabilito nelle «Norme
tecniche per il progetto sismico di opere di fondazione e di sostegno dei terreni» e dalle disposizioni
vigenti, in particolare dal D.M. 11.3.1988 ed eventuali sue successive modifiche ed integrazioni.
Scopo delle indagini sarà anche quello di classificare il terreno.
Per costruzioni su pendii le indagini devono essere convenientemente estese al di fuori dell’area
edificatoria per rilevare tutti i fattori occorrenti alla valutazione delle condizioni di stabilità del
complesso opera-pendio in presenza delle azioni sismiche.
16
8
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Requisiti di sicurezza e criteri di verifica
LIVELLI DI PROTEZIONE SISMICA
Le costruzioni devono essere dotate di un livello di protezione sismica differenziato in funzione della
loro importanza e del loro uso, e quindi delle conseguenze più o meno gravi di un loro
danneggiamento per effetto di un evento sismico. A tale scopo si istituiscono diverse «categorie di
importanza», a ciascuna delle quali è associato un fattore ? ? detto fattore di importanza.
Tale fattore amplifica ’lintensità della azione sismica di progetto rispetto al valore che per essa
si assume per costruzioni di importanza ordinaria (azione sismica di riferimento).
Il fattore di importanza si applica in eguale misura all’azione sismica da adottare per lo stato limite di
collasso e per lo stato limite di danno, variando conseguentemente le probabilità di occorrenza dei
relativi eventi.
17
La progettazione sismica delle strutture
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
18
9
Definizione dei livelli di azione sismica
Fattori che influenzano il moto sismico
19
Definizione dei livelli di azione sismica
Fattori che influenzano il moto sismico
Tipologie della frattura:
a) a trazione
b) a compressione
c) a taglio
Caratteristiche della sorgente sismica
20
10
Definizione dei livelli di azione sismica
Fattori che influenzano il moto sismico
Distanza epicentrale
21
Definizione dei livelli di azione sismica
Fattori che influenzano il moto sismico
• la direzione del processo di rottura della faglia influenza
maggiormente le zone near-field, mentre le stratificazioni del suolo
influenzano le proprietà delle onde sismiche per le zone far-field.
• per le zone near-field il moto sismico è di tipo impulsivo a bassa
frequenza in accelerazione e con pronunciati picchi nello spettro
delle velocità e degli spostamenti. Normalmente la durata
dell’evento sismico è breve. Per zone far-field le registrazioni del
moto sismico in termini di accelerazione, velocità e spostamento ha
le caratteristiche di un evento ciclico di lunga durata.
• La componente verticale del moto sismico in zone near-field può
anche essere maggiore della componente orizzontale a causa della
propagazione diretta delle onde di tipo P, poco influenzate dalla
condizione e tipologia del terreno.
• Le velocità del terreno durante un evento sismico per zone nearfield è il principale parametro della progettazione; mentre per zone
far-field l’accelerazione al suolo rimane il parametro essenziale di
progetto.
22
11
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
CATEGORIE DI SUOLO DI FONDAZIONE
Ai fini della definizione della azione sismica di progetto si definiscono le seguenti categorie di profilo
stratigrafico del suolo di fondazione (le profondità si riferiscono al piano di posa delle fondazioni):
A Formazioni litoidi o suoli omogenei molto rigidi caratterizzati da valori di velocità VS30 superiori
a 800 m/s, comprendenti eventuali strati di alterazione superficiale di spessore massimo pari a 5
metri.
B Depositi di sabbie o ghiaie molto addensate o argille molto consistenti, con spessori di
diverse decine di metri, caratterizzati da un graduale miglioramento delle proprietà meccaniche
con la profondità e da valori di VS30 compresi tra 360 m/s e 800 m/s (ovvero resistenza
penetrometrica NSPT > 50, o coesione non drenata cu > 250 kPa).
C Depositi di sabbie e ghiaie mediamente addensate, o di argille di media consistenza, con
spessori variabili da diverse decine fino a centinaia di metri, caratterizzati da valori di VS30
compresi tra 180 e 360 m/s (15 < NSPT < 50, 70 < cu < 250 kPa).
D Depositi di terreni granulari da sciolti a poco addensati oppure coesivi da poco a mediamente
consistenti, caratterizzati da valori di VS30 < 180 m/s (NSPT < 15, cu < 70 kPa).
23
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
CATEGORIE DI SUOLO DI FONDAZIONE
E
Profili di terreno costituiti da strati superficiali alluvionali, con valori di VS30 simili a
quelli dei tipi C o D e spessore compreso tra 5 e 20 m, giacenti su di un substrato di materiale
più rigido con VS30 > 800 m/s.
In aggiunta a queste categorie, per le quali vengono definite le azioni sismiche da considerare nella
progettazione, se ne definiscono altre due, per le quali sono richiesti studi speciali per la definizione
dell’azione sismica da considerare:
S1 Depositi costituiti da, o che includono, uno strato spesso almeno 10 m di argille/limi
di bassa consistenza, con elevato indice di plasticità (PI > 40) e contenuto di acqua, caratterizzati
da valori di VS30 < 100 m/s (10 < cu < 20 kPa).
S2 Depositi di terreni soggetti a liquefazione, di argille sensitive, o qualsiasi altra categoria
di terreno non classificabile nei tipi precedenti.
24
12
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
CATEGORIE DI SUOLO DI FONDAZIONE
Nelle definizioni precedenti VS30 è la velocità media di propagazione entro 30 m di profondità
delle onde di taglio e viene calcolata con la seguente espressione:
dove hi e V i indicano lo spessore (in m) e la velocità delle onde di taglio (per deformazioni
di taglio ? < 10-6) dello strato i-esimo, per un totale di N strati presenti nei 30 m superiori.
Il sito verrà classificato sulla base del valore di V S30, se disponibile, altrimenti sulla base del
valore di NSPT.
25
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
CALCOLO DELL’AZIONE SISMICA
Zone sismiche
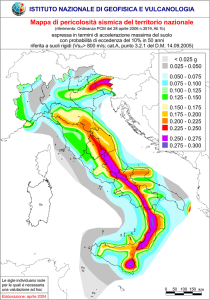
Ai fini dell’applicazione di queste norme, il territorio nazionale viene suddiviso in zone sismiche,
ciascuna contrassegnata da un diverso valore del parametro ag =accelerazione orizzontale massima su
suolo di categoria A. I valori di ag espressi come frazione dell’accelerazione di gravità g, da adottare
in ciascuna delle zone sismiche del territorio nazionale sono, salvo più accurate determinazioni, che
possono portare a differenze comunque non superiori al 20%:
26
13
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
CALCOLO DELL’AZIONE SISMICA
Zone sismiche
Zonazione D.G.P.
n. 2813 d.d. 23-102003
27
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Il modello di riferimento per la descrizione del moto sismico in un punto della superficie del
suolo è costituito dallo spettro di risposta elastico.
Per applicazioni particolari, il moto del suolo può essere descritto mediante accelerogrammi.
Il moto orizzontale è considerato composto da due componenti ortogonali indipendenti,
caratterizzate dallo stesso spettro di risposta.
In mancanza di documentata informazione specifica, la componente verticale del moto sismico
si considera rappresentata da uno spettro di risposta elastico diverso da quello delle componenti
orizzontali.
28
14
Lo spettro di risposta
Modellazione dell’azione sismica
Rappresentazione del moto mediante spettro di risposta
Lo spettro di risposta rappresenta la curva interpolante i valori di
risposta (in termini di accelerazione, velocità o spostamento)
massimi di un sistema ad 1 grado di libertà in funzione del periodo
fondamentale del sistema stesso.
In altre parole immaginiamo di avere un sistema ad un grado di
libertà, nel quale possiamo far variare la rigidezza. Su questo sistema
risolviamo per integrazione l'equazione di moto, ottenendo la
risposta del sistema sottoposto ad una storia di accelerazioni. Della
risposta viene preso il valore massimo per ogni stato di rigidezza del
sistema.
Poiché la rigidezza di un sistema è strettamente correlata con il
periodo fondamentale, lo spettro in termini di accelerazione e'
quindi la curva che inviluppa i massimi di risposta, sempre in
termini di accelerazioni, in funzione del periodo fondamentale del
nostro sistema. L’ordinate dello spettro dipendono ovviamente dal
valore del rapporto di smorzamento ζ.
29
Lo spettro di risposta
Modellazione dell’azione sismica
Rappresentazione del moto mediante spettro di risposta
• Studiando la variazione del valore dell’accelerazione in funzione
del periodo T, si può notare come per T = 0, struttura rigida,
l’accelerazione massima della struttura coincide con la massima
accelerazione del moto del terreno.
• Al crescere del periodo l’accelerazione assoluta del sistema Sa
cresce, raggiungendo per T = Tprevail il suo valore massimo pari
solitamente a 2-6 volte l’accelerazione massima del suolo.
• Il valore massimo si raggiunge quando il sistema ad un grado di
libertà è caratterizzata da periodo naturale prossimo al valore T
prevail, per cui si trova in condizioni di risonanza.
• I terremoti crostali (intraplate), più frequenti sono caratterizzati da
frequenze dominanti intorno ai 0.2-0.4 s, che corrispondono in
genere al periodo naturale di edifici bassi (2-4 piani).
• I terremoti profondi (interplate), invece, hanno frequenze
dominanti intorno ad 1.0-2.0 s, che corrispondono al periodo
fondamentale di edifici alti (10-20 piani).
30
15
Lo spettro di risposta
Modellazione dell’azione sismica
Rappresentazione del moto mediante spettro di risposta
Lo spettro delle accelerazioni, oltre a permettere una raffigurazione
globale della risposta strutturale, consente alcune considerazioni di
natura statica sull’azione sismica, che è essenzialmente un fenomeno
dinamico.
Infatti, ricordando la relazione tra forze d’inerzia e forze di reazione:
V = k (x − x0 ) = k u = - (c u& + M &x& )
è possibile ricavare il valore massimo del taglio alla base Vmax che si
realizza quando lo spostamento relativo raggiunge il suo valore
massimo, e quindi la velocità nulla:
Vmax = k umax ≅ M &x& max
Vmax = k S d = M Sa
Ponendo Vmax in funzione del peso della struttura, si ottiene la
seguente espressione:
Vmax
M Sa M Sa Sa
=C =
=
=
W
W
Mg
g
31
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettro di risposta elastico (componente orizzontale)
Lo spettro di risposta elastico è costituito da una forma spettrale (spettro normalizzato), considerata
indipendente dal livello di sismicità, moltiplicata per il valore della accelerazione massima (ag S) del
terreno che caratterizza il sito.
Lo spettro di risposta elastico della componente orizzontale è definito dalle espressioni seguenti:
32
16
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettro di risposta elastico (componente orizzontale)
S
η
fattore che tiene conto del profilo stratigrafico del suolo di fondazione;
fattore che tiene conto di un coefficiente di smorzamento viscoso equivalente ?, espresso in
punti percentuali, diverso da 5 (? = 1 per ? = 5):
T
periodo di vibrazione dell’oscillatore semplice;
TB , TC, TD periodi che separano i diversi rami dello spettro, dipendenti dal profilo stratigrafico
del suolo di fondazione.
33
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettro di risposta elastico (componente verticale)
34
17
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettro di risposta elastico
Se / ag
4,0
3,5
D
3,0
B-C-E
A
Verticale
2,5
2,0
1,5
1,0
0,5
0,0
0
1
2
T (s)
3
4
35
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettro di risposta elastico (spostamento)
Lo spettro di risposta elastico dello spostamento potrà ottenersi per trasformazione diretta
dello spettro di risposta elastico delle accelerazioni, usando la seguente espressione:
Gli spettri sopra definiti potranno essere applicati per
periodi di vibrazione che non eccedono 4,0 s. Per periodi
superiori lo spettro dovrà essere definito da appositi
Spettro di risposta elastico dello spostamento
0,16
studi.
D
0,14
Sde / ag
Nei casi in cui non si possa valutare adeguatamente
l’appartenenza del profilo stratigrafico del suolo di
fondazione ad una delle categorie di cui al punto 3.1, ed
escludendo comunque i profili di tipo S1 e S2, si adotterà
in generale la categoria D o, in caso di incertezza di
attribuzione tra due categorie, la condizione più
cautelativa.
B-C-E
0,12
A
0,10
Verticale
0,08
0,06
0,04
0,02
0,00
0
1
2
T (s)
3
4
36
18
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spostamento e velocità del terreno
I valori dello spostamento e della velocità orizzontali massimi del suolo (dg) e (ν g) sono dati
dalle seguenti espressioni:
dg = 0,025 · S · TC · TD · ag
ν g = 0,16 S · TC · ag
Spettri di progetto per lo stato limite ultimo
Ai fini del progetto, le capacità dissipative delle strutture possono essere messe in conto attraverso
un fattore riduttivo delle forze elastiche, denominato fattore di struttura q. L’azione sismica
di progetto Sd(T) è in tal caso data dallo spettro di risposta elastico, con le
ordinate ridotte utilizzando il fattore q.
I valori numerici del fattore q vengono definiti in funzione dei materiali e delle tipologie strutturali.
37
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettri di progetto per lo stato limite ultimo
Lo spettro di progetto per le componenti orizzontali è definito dalle seguenti espressioni:
Si assumerà comunque Sd(T) = 0,2 ag .
38
19
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettri di progetto per lo stato limite ultimo
A meno di adeguate analisi giustificative, lo spettro di progetto della componente verticale dell’azione
sismica è dato dalle seguenti espressioni, assumendo q = 1,5 per qualunque tipologia strutturale e di
materiale:
39
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettri SLU - qh=4,5 - qv=1,5
2,0
D
B-C-E
A
Verticale
Se / ag
1,6
1,2
0,8
0,4
0,0
0
1
2
T (s)
3
4
40
20
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Spettro di progetto per lo stato limite di danno
Lo spettro di progetto da adottare per la limitazione dei danni può essere ottenuto riducendo lo
spettro elastico secondo un fattore pari a 2,5.
Impiego di accelerogrammi
Entrambi gli stati limite di collasso e di danno potranno essere verificati mediante l’uso di
accelerogrammi artificiali o simulati o naturali. Quando è necessario utilizzare un modello spaziale,
l’azione sismica deve essere rappresentata da gruppi di tre accelerogrammi diversi agenti
contemporaneamente nelle tre direzioni principali della struttura.
Gli accelerogrammi dovranno avere uno spettro di risposta coerente con lo spettro di risposta
elastico. La durata degli accelerogrammi dovrà essere stabilita sulla base della magnitudo e degli altri
parametri fisici che determinano la scelta del valore di ag e S. In assenza di studi specifici la durata
della parte pseudo-stazionaria degli accelerogrammi sarà almeno pari a 10 s.
Il numero di accelerogrammi o, per analisi spaziali, di gruppi di accelerogrammi deve essere almeno
pari a 3.
41
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Combinazione dell’azione sismica con altre azioni
La verifica allo stato limite ultimo (SLU) o di danno (SLD) deve essere effettuata per la seguente
combinazione degli effetti della azione sismica con le altre azioni:
dove:
?i
GK
PK
? ji(? 2i)
? 0i
Qki
E azione sismica per lo stato limite in esame;
carichi permanenti al loro valore caratteristico;
valore caratteristico dell’azione di precompressione, a cadute di tensione avvenute;
coefficiente di combinazione che fornisce il valore quasi-permanente della azione
variabile Qi;
coefficiente di combinazione che fornisce il valore raro dell’azione variabile Qi;
valore caratteristico della azione variabile Qi.
42
21
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Combinazione dell’azione sismica con altre azioni
Gli effetti dell’azione sismica saranno valutati tenendo conto delle masse associate ai seguenti
carichi gravitazionali:
dove:
? Ei
coefficiente di combinazione dell’azione variabile Qi, che tiene conto della probabilità che
tutti i carichi ? 2iQKi siano presenti sulla intera struttura in occasione del sisma, e si ottiene
moltiplicando ? 2i per ϕ.
I valori dei coefficienti ? 2i e ϕ sono riportati nelle successive tabelle.
43
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Fattori di importanza
Gli edifici sono suddivisi in tre categorie, cui corrispondono le definizioni ed i fattori
di importanza indicati nella tabella seguente:
44
22
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Azione sismica
DESCRIZIONE DELL’AZIONE SISMICA
Combinazione dell’azione sismica con altre azioni
COEFFICIENTI ψ2i PER VARIE DESTINAZIONI D’USO
Destinazione d’uso
? 2i
Abitazioni, Uffici
0,30
Uffici aperti al pubblico, Scuole, Negozi,
Autorimesse
0,60
Tetti e coperture con neve
0,20
Magazzini, Archivi, Scale
0,80
Vento
0,00
45
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Confronto con la precedente normativa sismica
NORMATIVA SISMICA alle Tensioni Ammissibili (T.A.)
• Verifica convenzionale e prescrittiva;
• Assunzione della normativa è che una struttura in grado di sopportare in regime elastico le forze
corrispondenti all’accelerazione di progetto (definita per un tempo di ritorno di 50-100 anni, pari
alla vita utile della struttura) dovrebbe essere in grado di resistere, senza crollare, ai terremoti più
severi con tempi di ritorno di alcuni secoli;
• Massima accelerazione al suolo CR = 0.1 g.
ORDINANZA 3274 (20 Marzo 2003 e successive modifiche)
• Verifica prestazionale esplicita;
• La struttura deve essere progettata per resistere ad un sisma con periodo di ritorno di 475 anni
(S.L.U.) e per non danneggiarsi per un sisma con periodo di ritorno di 95 anni (S.L.D.);
• Massima accelerazione al suolo 0.35 g.
46
23
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Confronto con la precedente normativa sismica
NORMATIVA SISMICA alle Tensioni Ammissibili (T.A.)
Calcolo della forza sismica: Fh,DM96 =γ E
S−2
⋅ R ⋅ I ⋅ε ⋅β ⋅Wt
100
Valutazione dei pesi sismici (masse oscillanti): Wt = Gi + sQi
con:
• S grado di sismicità (S = 6÷12);
• R coefficiente di risposta dipendente dal periodo di vibrazione T0
• I coefficiente di protezione sismica
• ε coefficiente di fondazione (normalmente pari a 1)
• β coefficiente di struttura (normalmente pari a 1)
• s coefficiente dipendente dalla destinazione d’uso (s = 0.33÷1)
47
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Confronto con la precedente normativa sismica
ORDINANZA 3274 (20 Marzo 2003 e successive modifiche)
Calcolo della forza sismica: Fh,OPCM03 =γ I
λ ⋅ α ⋅ S ⋅ 2,5
Wt
q
Valutazione dei pesi sismici (masse oscillanti): Wt = Gk + ψ EQk
con:
• λ coefficiente dipendente dalla struttura (pari a 0.85 ÷ 1)
• α ag/g rapporto tra accelerazione di progetto e accelerazione di gravità
• S fattore dipendente dal profilo stratigrafico del terreno
• q coefficiente di struttura
• ψ E coefficiente di combinazione dipendente dalla destinazione d’uso
48
24
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Confronto con la precedente normativa sismica
Confrontando le due formule analizzate ed eliminando i coefficiente di valore uguale o significato
simile si ottiene:
qDM96 =
α ⋅ 2.5
S −2 
γE 

 100 
Coefficiente di comportamento implicito!!!
DM 12/01/96
OPCM 25/03/03
categoria
S
C
γeC
Zona
α = ag/g
α2.5
III
II
I
6
9
12
0.04
0.07
0.1
0.06
0.105
0.15
3
2
1
0.15
0.25
0.35
0.375
0.625
0.875
q
implicito
6.3
6.0
5.8
⇒ Risulta evidente che l'uso del DM 12/01/96 implica sempre l’ uso di un fattore di struttura
prossimo a 6, senza fornire chiari dettagli costruttivi e verifiche appropriate per gli elementi
strutturali.
⇒ E’ questa la differenza tra verifica convenzionale e prestazionale esplicita!
49
La progettazione sismica delle strutture
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
50
25
Definizione dei criteri di progetto
Regolarità strutturale
Le strutture sono definite “regolari” quando:
• possiedono una distribuzione uniforme della resistenza, della
rigidezza, della massa e delle dimensioni di piano lungo la loro
altezza;
• sono caratterizzate da una distribuzione simmetrica di massa
e della rigidezza in pianta.
L’irregolarità verticale può essere dovuta da:
• una non uniforme distribuzione della rigidezza o resistenza;
• presenza di elementi di diversa rigidezza
• presenza di piani deboli (soft storey);
• improvvisa variazione della massa di piani adiacenti
• presenza di rientranze o sporgenze della struttura;
• irregolarità nella topografia del terreno.
51
Definizione dei criteri di progetto
Regolarità strutturale
La regolarità di un edificio condiziona la capacità dell’ingegnere di prevedere il comportamento
strutturale, la qualità di tale comportamento ed il costo necessario per renderlo accettabile. Il termine
regolarità racchiude in sé due concetti distinti:
• semplicità strutturale: esistenza di percorsi chiari e diretti per la trasmissione delle azioni dal punto
in cui esse sono applicate fino alle fondazioni. Essa consente una facilità di dimensionamento, di
modellazione, di analisi della struttura e di definizione dei dettagli costruttivi.
• uniformità: si intende contemporaneamente distribuzione uniforme dei carichi (verticali o sismici)
e una uniforme distribuzione degli elementi resistenti. In particolare, durante la progettazione
sismica occorre curare:
ü l’uniformità delle masse, perché l’azione sismica è proporzionale alla distribuzione delle masse
presenti;
ü l’uniformità delle rigidezze , perché in fase elastica l’azione sismica si distribuisce tra gli elementi
in proporzione alle loro rigidezze (S.L.D.);
ü l’uniformità delle resistenze e delle duttilità, perché queste condizionano il comportamento quando
si supera la fase elastica (S.L.U.).
52
26
Definizione dei criteri di progetto
53
Definizione dei criteri di progetto
Configurazione della struttura
Per un corretta configurazione della struttura devono essere esaminati due aspetti
fondamentali:
• l’interazione di tutte le componenti strutturali durante l’azione sismica;
• la corrispondenza tra il comportamento reale della struttura e quello supposto durante
il progetto in termini di rigidezza, resistenza e duttilità.
Una corretta progettazione sismica deve prevedere soluzioni adeguate per tre
componenti fondamentali:
1.
2.
3.
fondazioni;
solai;
sistema strutturale.
54
27
Definizione dei criteri di progetto
Configurazione della struttura
Fondazioni
Superficiali e profonde
Dal punto di vista sismico occorre
interconnettere tutti gli elementi in
modo da ridurre i movimenti relativi e
progettare gli elementi di fondazioni
sovraresistenti rispetto al resto della
struttura.
55
Definizione dei criteri di progetto
Configurazione della struttura
Solai
Devono essere sufficientemente rigidi
da garantire un’efficace ed uniforme
distribuzione dell’azione sismica fra gli
elementi verticali resistenti.
I solai devono rimanere in fase elastica
durante il terremoto in modo da
garantire un’adeguata distribuzione
dell’azione sismica.
Le aperture orizzontali nei solai
devono
essere
adeguatamente
controllate in modo da non provocare
riduzioni di rigidezza o rotture lungo
linee di minor resistenza.
56
28
Definizione dei criteri di progetto
Sistema strutturale
La scelta della tipologia gioca un ruolo
fondamentale nelle progettazione strutturale.
1. telaio tipo “shear type”
2. sistemi a parete
3. Sistemi a telaio con controventi
4. Sistemi a telaio “moment reisisting”
57
Definizione dei criteri di progetto
Sistema strutturale
Telai con controventi concentrici
a)
b)
c)
a)Controventi ad X
b) Controventi a V rovescia
c) Controvento a V
d) Controvento con diagonali
d)
e) Controvento a K
e)
58
29
Definizione dei criteri di progetto
Sistema strutturale
Telai con controventi concentrici
- elevata rigidezza alle azioni;
- instabilità degli elementi compressi;
- regime non-lineare fortemente influenzato
dal comportamento post-critico dell’asta
instabilizzata;
- rigidezza e capacità isteretiche decrescono
rapidamente all’aumentare delle escursioni
cicliche in campo plastico.
H
H
Tipico comportamento isteretico di un controvento concentrico
59
Definizione dei criteri di progetto
Sistema strutturale
Telai con controventi eccentrici
La lunghezza e geometria del collegamento eccentrico governano il comportamento post-elastico
del sistema e modalità di collasso;
1. se la zona “e” è grande, l’energia è dissipata sviluppando deformazioni plastiche flessionali;
2. se la zona “e” è piccola, l’energia è dissipata sviluppando deformazioni plastiche a taglio.
stiffening plates
e
I meccanismi plastici dissipativi
sono efficienti nell’assorbire le
azioni prodotte dai terremoti
caratterizzati da un grande periodo
di ritorno, ma richiedono eccessive
deformazioni
nelle
travi
d’impalcato
Configurazione tipica di un collegamento eccentrico sollecitato a taglio
60
30
Definizione dei criteri di progetto
Sistema strutturale
Plastic hinges
Telai privi di controventi
- La rigidezza alle azioni orizzontali è
governata dalla deformabilità flessionale
delle travi, delle colonne e, nel caso di
collegamenti semi-rigidi, anche dalla
deformabilità del nodo trave-colonna.
- Tale tipologia possiede grande flessibilità
architettonica ed una regolarità strutturale
verticale; essa è divenuta molto popolare
nelle regioni a forte sismicità, innanzitutto
per la sua elevata duttilità e per la stabilità
dimostrata per azioni cicliche .
- Disponibilità di un gran numero di
potenziali zone plastiche, che possono
formarsi nel nodo trave-colonna oppure
nelle
travi,
aumentando
così
la
predisposizione
della
struttura
alla
dissipazione energetica.
Struttura a telaio priva di controventi
con localizzazione ottimale delle zone plastiche
61
Definizione dei criteri di progetto
Errori di progettazione:
[Fonte: NISEE, National Information Service for Earthquake
Engineering, University of California, Berkeley]
mancanza di un adeguato ancoraggio in fondazione
62
31
Definizione dei criteri di progetto
Errori di progettazione:
mancanza di un adeguato ancoraggio delle barre di armatura
63
Definizione dei criteri di progetto
Errori di progettazione:
irregolarità nella rigidezza e resistenza delle colonne
64
32
Definizione dei criteri di progetto
Errori di progettazione:
influenza degli elementi non strutturali
65
Definizione dei criteri di progetto
Errori di progettazione:
meccanismo “soft storey”
66
33
Definizione dei criteri di progetto
Errori di progettazione:
irregolarità strutturale
67
Definizione dei criteri di progetto
Errori di progettazione:
irregolarità strutturale
68
34
Definizione dei criteri di progetto
Errori di progettazione:
irregolarità strutturale
69
Definizione dei criteri di progetto
Errori di progettazione:
irregolarità strutturale
70
35
Definizione dei criteri di progetto
Errori di progettazione:
irregolarità strutturale
71
Definizione dei criteri di progetto
Errori di progettazione:
effetti torsionali non previsti
72
36
Definizione dei criteri di progetto
Errori di progettazione:
progettazione inadeguata in termini
di resistenza, rigidezza o duttilità
73
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: i sistemi costruttivi
l Sistema costruttivo
Sotto - sistema strutturale
Edifici
con struttura in cemento
a telaio; armato a pareti; misto a telai e pareti; a nucleo; a ossatura
pendolare in acciaio; con pareti o nuclei che costituiscono il sistema
resistente principale per le azioni orizzontali; prefabbricato.
Edifici
con struttura in acciaio
a telaio; a telaio con controventi concentrici; a telaio con controventi
eccentrici; a mensola; intelaiato controventato.
Edifici con struttura mista
in acciaio e calcestruzzo
a telaio; a telaio con controventi concentrici; a telaio con controventi
eccentrici; a mensola; intelaiato controventato.
Edifici
con struttura in muratura
a pareti in muratura ordinaria; a pareti in muratura armata.
Edifici con struttura in legno
Edifici isolati
Edifici esistenti
74
37
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: distanze ed altezze
L’altezza massima (H) degli edifici di nuova costruzione è specificata nella tabella seguente, in
funzione del sistema costruttivo e della zona sismica.
Zona sismica
4
Sistema costruttivo
3
1
Altezza massima consentita (in m)
Edifici con struttura in
calcestruzzo
Edifici con struttura in acciaio
2
nessuna limitazione
nessuna
limitazione
nessuna limitazione
Edifici con struttura mista in
acciaio e calcestruzzo
nessuna limitazione
Edifici con struttura
in muratura ordinaria
16
11
7.5
Edifici con struttura in
muratura armata
25
19
13
Edifici con struttura in legno
10
7
7
75
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: distanze ed altezze
L’altezza di nuovi edifici in zona 1 e 2, prospicienti su strade, non può comunque superare i
seguenti limiti:
- per strade L < 11 m H = L
- per strade con L > 11 m H = 11 + 3 (L - 11)
La larghezza L si intende calcolata tra il contorno dell’edificio ed il ciglio opposto della strada
compresa la carreggiata.
L’altezza H dell’edificio è la massima differenza di livello tra il piano di copertura più elevato
ed il terreno, nelle immediate vicinanze dell’edificio.
Il contorno dell’edificio è la proiezione in pianta del fronte dell’edificio stesso, escluse le
sporgenze di cornici e balconi aperti.
La strada è l’area di uso pubblico aperta alla circolazione dei pedoni e dei veicoli, nonché
lo spazio identificabile non cintato aperto alla circolazione pedonale.
Il ciglio è la linea limite della sede stradale o dello spazio aperto alla circolazione pedonale.
76
38
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: distanze ed altezze
Nel caso di edifici costruiti su terreni in pendio, le altezze indicate possono essere incrementate di 1.5
m, a condizione che la media delle altezze di tutti i fronti rientri nei limiti indicati.
Due edifici possono essere costruiti a contatto solo nel caso in cui sia realizzata una
completa solidarietà strutturale.
La distanza tra due edifici contigui non può essere inferiore alla somma degli spostamenti massimi a
collasso calcolati per ciascuno degli edifici, secondo le modalità indicate per ciascun tipo strutturale.
In ogni caso la distanza tra due punti degli edifici posti alla medesima altezza non potrà essere
inferiore ad 1/100 della quota dei punti considerati misurata dallo spiccato delle strutture in
elevazione.
77
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: caratteristiche generali degli edifici. Regolarità
Gli edifici devono avere quanto più possibile caratteristiche di:
•
•
•
•
semplicità;
simmetria;
iperstaticità;
regolarità.
Quest’ultima definita in base ai criteri di seguito indicati.
N.B: In funzione della regolarità di un edificio saranno richieste scelte diverse in relazione al
metodo di analisi e ad altri parametri di progetto.
Si definisce regolare un edificio che rispetti sia i criteri di regolarità in pianta sia i criteri di regolarità
in altezza.
78
39
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: caratteristiche generali degli edifici. Regolarità
Un edificio è regolare in pianta se tutte le seguenti condizioni sono rispettate:
a) la configurazione in pianta è compatta e approssimativamente simmetrica rispetto a due
direzioni ortogonali, in relazione alla distribuzione di masse e rigidezze;
La primaria fonte di irregolarità in pianta è la non coincidenza tra baricentro delle masse e baricentro
delle rigidezze. Questa è dovuta principalmente alla mancanza di simmetria della pianta
architettonica, anche se un corretto dimensionamento delle sezioni degli elementi strutturali
dovrebbe mirare a rendere lo schema bilanciato, cioè far coincidere i due centri anche in assenza di
simmetria.
A causa dell’eccentricità tra centro di massa e centro delle rigidezze (ex ed ey, rispettivamente in
direzione y e direzione x), il comportamento dinamico della struttura presenta un notevole
contributo rotazionale che non viene colto correttamente da analisi semplificate, anche se si utilizza
uno schema tridimensionale. La rotazione indotta dinamicamente può essere infatti ben diversa da
quella provocata da forze statiche, specialmente nel caso di strutture deformabili torsionalmente.
b) il rapporto tra i lati di un rettangolo in cui l’edificio risulta inscritto è inferiore a 4;
79
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: caratteristiche generali degli edifici. Regolarità
c)
eventuali rientri o sporgenze non superano il 25% della dimensione totale dell’edificio
nella direzione del rientro o della sporgenza;
d) i solai possono essere considerati infinitamente rigidi nel loro piano rispetto agli elementi
verticali.
È prassi comune considerare il solaio come un elemento infinitamente rigido nel suo piano e quindi
utilizzare un vincolo mutuo tra i nodi trave-colonna del telaio spaziale. Per fare questo, però, è
necessario verificare la rigidezza e la resistenza del solaio. Tale verifica richiede di analizzare
l’impalcato estratto dalla struttura e soggetto ad un insieme di forze equilibrato, calcolarne la
deformazione (con uno schema di lastra-piastra) ed infine confrontare le deformazioni relative tra
impalcati adiacenti con gli spostamenti relativi forniti dalla risoluzione del telaio spaziale (da EC8: tali
spostamenti non devono eccedere per più del 10% quelli calcolati con lo schema del telaio spaziale).
Sono causa principale di irregolarità nel comportamento del solaio:
• grosse rientranze o parti mancanti, che riducono localmente la resistenza e rendono quindi
possibili elevate deformazioni;
• presenza di un numero molto basso di elementi verticali (colonne, pareti o nuclei irrigidenti);
• brusca variazione di rigidezza degli elementi resistenti verticali tra un piano e ’laltro, che
comporta la necessità di trasferire azioni rilevanti nell’impalcato.
80
40
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: caratteristiche generali degli edifici. Regolarità
Un edificio è regolare in altezza se tutte le seguenti condizioni sono rispettate:
e)
tutti i sistemi resistenti verticali dell’edificio (quali telai e pareti) si estendono per tutta l’ altezza
dell’edificio;
f)
massa e rigidezza rimangono costanti o si riducono gradualmente, senza bruschi cambiamenti,
dalla base alla cima dell’edificio (le variazioni da un piano all’altro non superano il 20%);
g)
il rapporto tra resistenza effettiva e resistenza richiesta dal calcolo non è significativamente
diverso per piani diversi (il rapporto fra la resistenza effettiva e quella richiesta calcolata ad un
generico piano non deve differire più del 20% dall’analogo rapporto determinato per un altro
piano);
h) eventuali restringimenti della sezione dell’edificio avvengono in modo graduale, rispettando i
seguenti limiti: ad ogni piano il rientro non supera il 30% della dimensione corrispondente al
primo piano, né il 10% della dimensione corrispondente al piano immediatamente sottostante.
81
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: caratteristiche generali degli edifici. Regolarità
82
41
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Definizione dei criteri di progetto: elementi strutturali secondari
Alcuni elementi strutturali dell’edificio possono venire definiti «secondari».
Sia la rigidezza che la resistenza di tali elementi viene ignorata nell’analisi della risposta.
Tali elementi tuttavia devono essere in grado di assorbire le deformazioni della struttura soggetta
all’azione sismica di progetto mantenendo la capacità portante nei confronti dei carichi verticali.
Regole di dettaglio idonee a soddisfare il requisito di cui sopra sono contenute nei capitoli relativi alle
diverse tipologie strutturali.
La scelta degli elementi da considerare secondari può essere cambiata a seguito di analisi preliminari,
ma in nessun caso tale scelta può determinare il passaggio da struttura «irregolare» a struttura
«regolare».
83
La progettazione sismica delle strutture
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
84
42
Scelta del modello strutturale
Una corretta progettazione strutturale presuppone un adeguato modello della struttura su cui
si esegue l’analisi strutturale, in cui sono considerati:
- comportamento dei materiali;
- comportamento degli elementi strutturali;
- comportamento dei collegamenti strutturali;
- la struttura nel suo complesso;
- l’interazione tra la struttura ed il terreno;
- comportamento spaziale della struttura;
- gli elementi non-strutturali.
85
Scelta del modello strutturale
Materiale
Modelli costitutivi
(a) I legami costitutivi devono
considerare
il
comportamento
incrudente del materiale, poiché
durante i terremoti violenti le
deformazioni raggiungono tali valori.
(b) Nelle leggi costitutive cicliche è
molto importante rappresentare i
fenomeni legati all’isteresi del
materiale.
(a)
(b)
86
43
Scelta del modello strutturale
Elementi strutturali
In accordo al concetto di struttura dissipativa,
alcune zone critiche degli elementi strutturali
possono essere scelte per l’ eventuale sviluppo
delle cerniere plastiche.
Queste zone devono essere appropriatamente
progettate per fornire sufficiente capacità
rotazionale, valutata usando delle leggi
momento-rotazione per carichi monotoni o
ciclici.
87
Scelta del modello strutturale
Collegamenti strutturali
Il modello del comportamento dei nodi
trave-colonna è realizzato tramite una curva
momento-rotazione, che rappresenta il reale
comportamento del nodo.
Per le strutture in acciaio:
- rigido
- semi-rigido
- incernierato
88
44
Scelta del modello strutturale
La struttura
Il comportamento dell’intera struttura può essere modellato come:
(a) sistema ad N gradi di libertà;
(b) un sistema equivalente ad un grado di libertà;
(c) un sistema a trave equivalente di sezione costante deformabile a taglio.
Modelli strutturali
(a)
(b)
(c)
89
Scelta del modello strutturale
Interazione terreno-struttura
L’interazione tra la struttura ed il
terreno deve tenere in conto:
(a) la possibilità di avere spostamenti
verticali ed orizzontali differenti tra i
vincoli della struttura;
(b) modifiche del periodo proprio della
struttura dovute all’interazione;
(c) cambiamento del moto del terreno
alla base rispetto al moto in campo
libero.
90
45
Scelta del modello strutturale
Comportamento spaziale
Eccentricità “statiche” tra il centro
di massa ed il centro di rigidezza, ed
eccentricità accidentali, causate da
moti asincroni del terreno, causano
fenomeni torsionali che conducono
ad un incremento delle forze
interne.
Il comportamento post-elastico
della struttura causa lo spostamento
del
centro
di
rigidezza,
incrementando
gli
eventuali
fenomeni torsionali.
91
Scelta del modello strutturale
Gli elementi non strutturali
(a) Tamponature in lamiera
(b) Tamponature in muratura
incrementano notevolmente la rigidezza
laterale della struttura e dovrebbero essere
tenute in conto durante il progetto.
Il modello più utilizzato è quello di
sostituire agli elementi di tamponamento dei
controventi equivalenti (c).
Il tamponamento è schematizzato, quindi,
come
un elemento che lavora
esclusivamente in compressione, la cui
rigidezza può essere determinata con la
seguente espressione:
K w = 0.6
Ew ⋅ w ⋅ t ⋅ cos 2 θ
d
92
46
La progettazione sismica delle strutture
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
93
Analisi strutturale
Richiami di dinamica strutturale: sistemi a più gradi di libertà
Le strutture tipiche dell’ingegneria civile non sono sempre schematizzabili come semplici sistemi
ad un grado di libertà (SDoF). Bisogna fare spesso ricorso a modelli più complessi, con molteplici
gradi di libertà (MDoF). Nel caso frequente di edifici multipiano con solai rigidi nel piano, è
possibile schematizzare la struttura considerando le masse concentrate nei piani e assumendo
come gradi di libertà il minimo numero di spostamenti e rotazioni indipendenti delle masse
concentrate.
Se si ipotizza, quindi, un edificio di n piani con diaframmi orizzontali infinitamente rigidi nel loro
piano e colonne infinitamente rigide assialmente, il suo comportamento nello spazio sarà descritto
da 3 ´ n gradi di libertà (due spostamenti orizzontali secondo direzioni ortogonali e una
rotazione attorno all’asse verticale per piano); se ci si limita allo studio nel piano, questi si
ridurranno a n gradi di libertà, pari ai soli spostamenti orizzontali dei piani.
94
47
Analisi strutturale
Richiami di dinamica strutturale: sistemi a più gradi di libertà
Edificio a 5 piani con solai rigidi nel piano (5 G.d.L.)
(a) modello piano;
(b) modello con masse concentrate;
(c) modi propri di vibrare normalizzati rispetto al massimo spostamento.
95
Analisi strutturale
Richiami di dinamica strutturale: sistemi a più gradi di libertà
Elemento fondamentale nell’analisi dinamica di sistemi MDoF è l’individuazione dei modi propri
di vibrare: essi, in numero pari al numero di gradi di libertà della struttura, costituiscono le
oscillazioni periodiche libere del sistema elastico non smorzato.
La loro combinazione lineare definisce la posizione del sistema ad ogni istante.
In ciascun modo tutte le masse del sistema oscillano con la medesima pulsazione ed in fase,
mantenendo immutati i rapporti tra le ampiezze.
Ciò implica che per ogni oscillazione le masse passano attraverso il punto di massimo
spostamento allo stesso istante.
Per calcolare i modi propri di vibrare si utilizzano gli strumenti dell’analisi modale.
96
48
Analisi strutturale
Nei sistemi schematizzabili con modelli piani, il modo proprio con periodo più lungo è
definito il modo fondamentale o primo modo; nel caso di modelli spaziali si considerano i
tre periodi più lunghi associati rispettivamente ai due modi traslazionali e a quello rotazionale.
97
Analisi strutturale
Per ottenere la risposta del sistema
si
utilizzano
delle
tecniche
di
combinazione dei modi derivanti
dall’analisi
probabilistica.
Ricordando inoltre che le masse
modali
dei
generalmente
primi
modi
sono
preponderanti,
si
deduce che per un’analisi modale
con spettro di risposta può essere
sufficiente considerare solo i primi
modi.
98
49
Analisi strutturale
Metodi di analisi strutturale
99
Analisi strutturale
Metodo (elastico) della forza laterale equivalente
E’ il primo e più semplice metodo di analisi sismica delle strutture. E’ basato sull’assunzione che il
comportamento della struttura è governato dal suo periodo fondamentale di vibrazione e della
relativa forma modale. L’analisi strutturale risulta conservativa per edifici di piccola e media altezza
con caratteristiche di regolarità strutturale. La distribuzione delle forze laterali segue la forma del
primo modo .
Le caratteristiche del moto sono descritte
tramite lo spettro di risposta elastico, che
definisce l’ accelerazione che deve essere
sostenta dall’edificio se progettato in
modo da rimanere in campo elastico. Per
far ricorso anche alle risorse inelastiche
della struttura, è possibile ridurre le
ordinate dello spettro in ragione del
fattore di struttura q.
100
50
Analisi strutturale
Metodo (elastico) della forza laterale equivalente
Questo tipo di analisi trova il suo fondamento nel fatto che in molte strutture la massa efficace
% risulta essere preponderante (fino all’80-90% della massa totale) rispetto
relativa al primo modo W
i
alle altre e la corrispondente ordinata spettrale è maggiore o uguale a quella degli altri modi. Infatti
sotto queste ipotesi essendo la forza di taglio alla base dovuta all’i-esimo modo pari a:
% ⋅ S ( T ,ξ )
Fbi = g ⋅ W
i
a
i i
e quindi il taglio alla base può essere approssimato con la somma dei contributi modali:
in cui il contributo del primo modo alla forza totale sarà preponderante e sostituendo la massa
relativa al primo modo con la massa totale del sistema M si otterrà un’approssimazione per eccesso
della forza di taglio alla base Fb.
Questa approssimazione non è più valida qualora risulti Sa1<Sa2, Sa3 … cioè se il periodo
fondamentale del sistema è alto.
101
Analisi strutturale
Metodo (elastico) della forza laterale equivalente
Si veda ad esempio il caso rappresentato nella seguente figura:
Analisi con spettro di risposta di una struttura flessibile, caratterizzata da un modo fondamentale
elevato. La massa partecipante del primo modo risulta essere pari al 70% contro il 13% del secondo
modo ed il 6% del terzo.
102
51
Analisi strutturale
Metodo (elastico) della forza laterale equivalente
Come accade nella maggior parte dei casi, lo spettro di risposta utilizzato presenta per periodi
superiori ad un secondo(T1=1.5s) bassi valori dell’ordinata spettrale; in particolare Sa1=0.026s,
mentre le ordinate degli altri modi risultano pari a Sa2=0.32s e Sa3=0.36.
E’ immediato verificare che il contributo elastico del modo fondamentale
Fb1=0.026´0.7=0.018 risulta inferiore a quello del secondo e del terzo modo, rispettivamente
Fb2=0.32´0.13=0.04 e Fb3=0.36 ´ 0.06=0.022; approssimare il comportamento della struttura con
quello del primo modo provoca errori sia nel valore che nella distribuzione delle forze statiche
equivalenti e, ovviamente, nei risultati dell’analisi.
In questi casi, allora, il metodo della forza laterale equivalente non può essere applicato; si devono
utilizzare metodi più accurati, quali il metodo della sovrapposizione modale.
103
Analisi strutturale
Metodo (elastico) di sovrapposizione modale
La risposta del sistema a molti G.d.L. è espressa come la sovrapposizione di singole risposte modali,
determinate dallo spettro di risposta per il sistema ad 1 G.d.L.
Lo spettro di progetto è scalato per un fattore di struttura q costante per tutti i modi di vibrare
considerati. Gli effetti di ogni modo sono combinati in modo da ottenere una stima della risposta
strutturale complessiva.
104
52
Analisi strutturale
Metodo (elastico) di sovrapposizione modale
Questo tipo di analisi è considerato il metodo normale per la definizione delle sollecitazioni di
progetto. Deve essere applicato usando un modello tridimensionale della struttura a meno che non
siano rispettati i criteri di regolarità in pianta: in questo caso è sufficiente studiare due modelli piani
separati.
La maggior differenza con l’analisi statica equivalente consiste nel fatto che nel calcolo dei parametri
di risposta del sistema si tiene conto delle caratteristiche dinamiche della struttura tramite l’ utilizzo
dei modi propri di vibrare.
L’analisi modale, così come è solitamente applicata, prevede di calcolare, tramite ’lutilizzo dello
spettro di risposta di pseudo-accelerazione, i valori massimi di sollecitazioni e spostamenti associati
a ciascun modo proprio di vibrare della struttura supposta elastica lineare, e quindi di combinarli in
modo opportuno.
105
Analisi strutturale
Modellazione della risposta non-lineare
La capacità di una struttura di resistere all’evento sismico dipende fortemente dalle sue capacità
deformative e dalla sua duttilità.
I metodi di analisi elastici (statico e dinamico) tengono conto del comportamento non lineare della
struttura tramite il fattore di struttura che permette di ridurre lo spettro di risposta elastico.
Questi metodi non possono però cogliere cambiamenti nella risposta caratteristica della struttura
che si verificano man mano che singoli elementi si comportano in modo duttile.
Inoltre non si ha nessuna informazione sulla distribuzione della domanda di anaelasticità nella
struttura.
I metodi di analisi non lineare, invece, permettono di cogliere questi aspetti dimostrandosi un utile
strumento in particolare in fase di verifica, laddove è necessario valutare la coerenza fra fattori di
struttura assunti e reale capacità di duttilità della struttura.
106
53
Analisi strutturale
Modellazione della risposta non-lineare
Non linearità geometrica
Nella modellazione di strutture che subiscono elevati spostamenti e deformazioni, è necessario
tenere in conto la non linearità geometrica della risposta strutturale che causa una variazione degli
spostamenti non proporzionale ai carichi.
Infatti, quando un corpo elastico si deforma in modo significativo non è più valida l’ipotesi della
teoria dell’elasticità lineare secondo la quale è possibile, in un processo deformativo, confondere
configurazione iniziale (indeformata) e finale (deformata).
E’ possibile individuare tre principali cause di non linearità geometrica:
- Grandi spostamenti e rotazioni;
- Effetti del secondo ordine;
- Effetti trave-colonna.
[Rif. Bibl. Petrini, Pinho, Calvi, 2004. Criteri di progettazione
antisismica degli edifici. IUSS Press, Pavia]
107
Analisi strutturale
Modellazione della risposta non-lineare
Grandi spostamenti/Rotazioni
Per comprendere in che modo la presenza di grandi
spostamenti/rotazioni nella risposta della struttura
elastica renda non soddisfatte le ipotesi della teoria
della elasticità lineare, si consideri una mensola
caricata con una forza inizialmente in direzione
ortogonale all’asse.
Supporre che configurazione iniziale e finale coincidano, corrisponde a considerare il carico sempre
ortogonale all’asse della trave: il taglio crescerà linearmente con lo spostamento verticale dell’estremo
libero.
Se invece, come è anche intuibile fisicamente, si considera che, man mano che il carico cresce,
l’elemento cambia configurazione rispetto a quella iniziale, assunto solidale con il corpo un sistema di
riferimento locale, quest’ultimo risulterà ruotato rispetto alla direzione del carico agente in modo tale
che:
-a) la componente del carico ortogonale all’asse non crescerà più linearmente con lo spostamento;
-b) anche il momento di conseguenza crescerà non linearmente in quanto una quota del carico
diventerà azioni assiale.
108
54
Analisi strutturale
Modellazione della risposta non-lineare
Effetti del secondo ordine
Per comprendere in che modo la presenza di effetti del secondo
ordine nella risposta di una struttura elastica renda non soddisfatte le
ipotesi della teoria dell’elasticità lineare, si consideri un elemento
verticale soggetto ad un carico verticale V e ad un carico orizzontale
H tale da imporre uno spostamento δ.
Supporre che configurazione indeformata e deformata coincidano,
corrisponde a considerare il sistema di riferimento dell’elemento fisso
e, quindi, il carico verticale sempre parallelo all’asse della colonna: la
struttura sarà soggetta ad una azione assiale pari a V e ad un
momento flettente alla base pari ad H´h.
Se invece si considera che, a causa dello spostamento δ, l’elemento ha cambiato configurazione
rispetto a quella iniziale inflettendosi, assunto solidale con il corpo un sistema di riferimento locale,
quest’ultimo risulterà ruotato rispetto alla direzione dei carichi agenti in modo che il carico V
contribuirà anche al taglio ed incrementerà il momento flettente di V´δ.
109
Analisi strutturale
Modellazione della risposta non-lineare
Effetto trave-colonna
Per comprendere in che modo l’effetto travecolonna nella risposta di un elemento
strutturale elastico renda non soddisfatte le
ipotesi della teoria dell’elasticità lineare, si consideri un generico elemento soggetto contemporaneamente all’azione assiale ed al momento flettente.
Supporre che configurazione indeformata e deformata coincidano, corrisponde a considerare
completamente disaccoppiate le due azioni: azione assiale e momento produrranno sforzi e
deformazioni costanti lungo l’asse dell’elemento e, rispettivamente, uniformi e lineari sulla sezione.
Se invece si considera che, a causa dell’inflessione indotta dal momento, l’ elemento ha cambiato
configurazione rispetto a quella iniziale, risulterà una interazione tra la deformazione trasversale ed
azione assiale: in particolare un’azione assiale di compressione riduce la rigidezza flessionale, mentre
un’azione di trazione ha l’effetto opposto.
Questo si traduce in termini di modellazione, nell’avere una matrice di rigidezza dell’elemento in cui i
diversi contributi, assiale, flessionale e tagliante sono fra loro accoppiati.
110
55
Analisi strutturale
Modellazione della risposta non-lineare
Non linearità del materiale
L’importanza e la necessità di considerare la risposta in campo anelastico del materiale richiedono
l’utilizzo di programmi di calcolo in grado di descrivere la non linearità del materiale. I programmi
attualmente disponibili sono in grado di fare questo utilizzando due diversi approcci:
-
modellazione tramite cerniere plastiche (“a plasticità concentrata”): è stata la prima tecnica di
modellazione implementata in programmi di analisi strutturale per descrivere il comportamento
anaelastico di una struttura sotto l’azione ciclica del sisma. Essa prevede che tutti gli elementi
costituenti la struttura (generalmente elementi di tipo trave) rimangano sempre in campo
elastico e che vengano introdotti, alle estremità di questi, elementi cerniera con comportamento
anaelastico laddove si prevede la formazione della cerniera plastica.
-
modellazione tramite fibre (“a plasticità diffusa”).
111
Analisi strutturale
Modellazione della risposta non-lineare
Modellazione “a plasticità diffusa”
In questo caso si considerano elementi tipo trave con comportamento anaelastico: il
comportamento non lineare è diffuso in tutto ’lelemento strutturale, sia longitudinalmente che
trasversalmente, attraverso l’ utilizzo di elementi a fibre. Essi prevedono che lo stato di sforzodeformazione di una sezione del generico elemento sia ottenuto tramite integrazione della risposta
sforzo-deformazione uniassiale non lineare di ciascuna fibra in cui la sezione è stata suddivisa.
Una sezione in cemento armato può essere discretizzata tramite le “fibre”.
112
56
Analisi strutturale
Modellazione della risposta non-lineare
Metodi di analisi non-lineari
Questi metodi considerano la ri-distribuzione plastica delle sollecitazioni che avviene nelle strutture
iperstatiche per valori superiori al limite elastico.
Tali metodi consentono di ottenere il meccanismo di collasso della struttura sottoposta ad una
determinata distribuzione di azioni sismiche e di comprendere il comportamento della struttura in
prossimità del collasso.
Per lo studio del comportamento di una
struttura sottoposta a sollecitazioni
sismiche si possono applicare:
- analisi statica non lineare di tipo
“push-over”;
- analisi dinamica non lineare di tipo
incrementale.
113
Analisi strutturale
Modellazione della risposta non-lineare
Analisi statica non lineare “push-over”
Il metodo consiste in un’analisi statica incrementale non-lineare, con forze laterali di modulo
crescente distribuite lungo l’altezza. Il risultato è una curva che mette in relazione il moltiplicatore
dei carichi α con lo spostamento δ dell’ultimo piano della struttura.
Il metodo fornisce informazioni sulla resistenza, rigidezza e duttilità dell’intera struttura ed è
applicabile in modo efficace solo a strutture il cui moto è governato dal primo modo di vibrazione.
La capacità della struttura (definita Curva
di
Capacità)
è confrontata
con
la
domanda, rappresentata da punti sulla
curva stessa individuati in corrispondenza
di valori di spostamento corrispondenti
alle massime domande di spostamento
che la struttura subirebbe quando
soggetta ai diversi terremoti di progetto.
114
57
Analisi strutturale
Modellazione della risposta non-lineare
Analisi statica non lineare “push-over”
Al variare del tipo di distribuzioni e della modalità di applicazione delle forze laterali, della modalità
con cui si valuta lo spostamento prefissato e dei parametri di controllo utilizzati durante l’analisi, si
distinguono diversi tipi di analisi statica non lineare.
In particolare le norme, nel caso di struttura regolare e quindi descrivibile con due modelli piani
scelti secondo due direzioni ortogonali, suggeriscono, per la valutazione del legame taglio alla basespostamento di un punto di controllo, di applicare a ciascun modello piano considerato due diverse
distribuzioni di forze orizzontali applicate ai baricentri delle masse dei vari piani.
In particolare si possono considerare:
- una distribuzione di forze proporzionali alle masse;
-
una distribuzione di forze proporzionali alla prodotto delle masse per la deformata individuata
dal primo modo di vibrare del sistema considerato elastico.
115
Analisi strutturale
Modellazione della risposta non-lineare
Analisi statica non lineare “push-over”
Tale scelta nasce dalla considerazione che la distribuzione delle forze laterali dovrebbe approssimare
la distribuzione delle forze di inerzia presenti sulla struttura durante il sisma.
1.40
1.80g
2.00g
1.40g
2,0 g
1,8 g
1,4 g
1.20
1.00
0.80
V/W
0.60
0,25 g
0.40
0.25g
0,10 g
0.10g
0.20
0.00
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
4.00
4.50
5.00
δ /H
116
58
Analisi strutturale
Analisi tipo “Push-over” (statica non lineare)
La risposta caratteristica che può essere ottenuta con un’analisi statica non lineare comprende:
1. valutazione dei rapporti di sovraresistenza;
2. individuazione di una richiesta di resistenza su elementi fragili;
3. individuazione di una realistica richiesta di deformazione su elementi che devono avere un
comportamento duttile al fine di dissipare energia;
4. la possibilità di verificare l’effettiva distribuzione della domanda inelastica negli edifici
progettati con il fattore di riduzione q;
5. la possibilità di verificare le conseguenze della perdita di resistenza di un elemento sulla stabilità
dell’intera struttura;
6. individuazione delle zone critiche dove maggiore è la richiesta di duttilità;
7. individuazione di irregolarità in pianta o in altezza in termini di resistenza che modificano la
risposta dinamica in campo non lineare;
8. valutazione degli spostamenti relativi fra i piani tenendo conto delle discontinuità di resistenza
e rigidezza fra i piani.
117
Analisi strutturale
Analisi dinamica non-lineare
Il metodo analizza la risposta dinamica del modello strutturale per un moto alla base tramite
l’integrazione delle equazioni del moto.
Il comportamento elasto-plastico degli elementi strutturali è tenuto in conto. Tale metodo è l’unico
in grado di descrivere, se il modello è sufficientemente accurato, il reale comportamento della
struttura. L’onere di calcolo è elevato e l’accelerogramma del sisma deve essere scelto accuratamente
(spettro-compatibili).
118
59
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Metodi di analisi strutturali
Nelle norme sono ammessi quattro metodi di analisi caratterizzati da complessità e precisione
crescenti. Essi sono:
a)
b)
c)
d)
statica lineare (Analisi tramite la forza laterale equivalente)
dinamica modale (Metodo di sovrapposizione modale)
statica non lineare (Analisi tipo “Push-over”)
dinamica non lineare (Analisi dinamica non-lineare)
La scelta tra un metodo e l’altro dipende dalle caratteristiche (regolarità, periodi propri caratteristici) e
dall’importanza della struttura che si sta studiando. In particolare, le norme definiscono “metodo
normale”, per la definizione delle sollecitazioni di progetto, l’ analisi modale associata allo spettro di
progetto ed applicata ad un modello tridimensionale dell’edificio.
119
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Metodi di analisi strutturali
Considerazioni sulla regolarità in pianta ed in altezza della struttura permettono di considerare al
posto di un modello tridimensionale due modelli piani separati e al posto dell’analisi modale una
semplice analisi statica lineare, secondo quanto riassunto nella tabella:
Regolarità geometrica
Semplificazioni ammesse
Pianta
Altezza
Modello
Analisi
Sì
Sì
Piano
Statica lineare
Sì
No
Piano
Dinamica modale
No
Sì
Spaziale
Statica lineare
No
No
Spaziale
Dinamica modale
120
60
La progettazione sismica delle strutture
Un approccio progettuale esauriente deve prevedere i seguenti pa ssi:
- selezione dei livelli di prestazione richiesti;
- definizione dei livelli di verifica strutturale;
- determinazione dei livelli di azione sismica corrispondenti a ciascun
livello di verifica;
- definizione dei criteri di progetto;
- scelta del modello strutturale;
- selezione del tipo di analisi strutturale appropriato;
- definizione delle procedure di verifica.
[Rif. Bibl. Gioncu V., Mazzolani F.M., 2002. Ductility od
seismic resistant steel structures. Spon Press, New York]
121
La normativa italiana: l ’Ordinanza n. 3274 del 20/03/2003
Verifiche di sicurezza
Stato limite ultimo
Occorre verificare:
- le condizioni di resistenza;
- gli effetti dovuti ai fenomeni del secondo ordine;
- le condizioni di duttilità;
- le condizioni di equilibrio;
- la resistenza di eventuali diaframmi orizzontali;
- la resistenza delle fondazioni;
- le condizioni dei giunti sismici.
Stato limite di danno
Per evitare il collasso di elementi non strutturali per livelli di azione sismiche cui è associata
un’elevata probabilità di occorrenza, devono essere soddisfatte alcune limitazioni. Il cui parametro
di riferimento è solitamente lo spostamento relativo di inter-piano.
Misure specifiche
Per garantire un buon comportamento delle strutture per azioni sismiche anche più severe di quella
di riferimento, limitando allo stesso tempo le inevitabili incertezze legate alla progettazione, occorre
soddisfare ulteriori misure specifiche.
122
61