soluzioni

SOLUZIONI – SIMULAZIONE TEST GEOMETRIA
LA CIRCONFERENZA – I QUADRILATERI INSCRITTI E CIRCOSCRITTI – I PUNTI NOTEVOLI DEI TRIANGOLI
1.
A
2.
E
3.
A
4.
D
5.
B
6.
B
7.
8.
A
A
9.
A
10.
B
11.
D
A: Falsa - Ad ogni arco corrisponde una sola corda, ma ad ogni corda corrispondono due archi
B: Vera - Per tre punti allineati passano infinite circonferenza (quindi almeno una); per tre punti non
allineati passa una ed una sola circonferenza (quindi almeno una)
C: Vera – i due diametri, essendo congruenti e perpendicolari, sono le diagonali di un quadrato
D: Vera – il diametro è la corda di lunghezza massima
E: Vera – l’asse della corda è il luogo geometrico dei punti del piano equidistanti dagli estremi
Se allineati passa una ed una sola retta, se non allineati passa una ed una sola circonferenza
I) Vera: teorema
II) Vera: la proiezione del centro su una corda si ottiene tracciando la perpendicolare alla corda
passante per il centro; quindi per un teorema la proiezione del centro sulla corda è il punto medio
della corda
III) per il quinto postulato di Euclide
Le due circonferenze sono tangenti esternamente, quindi OO ' ≅ r + r '
I) Falsa: se l’angolo al centro è maggiore di 180°, l’angolo alla circonferenza corrispondente è ottuso
II) Falsa: ne esistono infiniti
III) Falsa: se l’angolo al centro è maggiore di 180°, l’angolo alla circonferenza corrispondente è
ottuso, quindi maggiore di un angolo retto
IV) Vera: perché la metà dell’angolo al centro di 180°
V) Vera: per definizione di angolo alla circonferenza
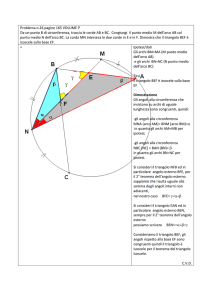
In riferimento alla figura si ha che OH < OP (in quanto OH è cateto di un
triangolo rettangolo di ipotenusa OP), quindi CD è una corda che ha distanza
dal centro minore della distanza di AB dal centro, quindi, per un teorema
dimostrato, CD > AB e quindi, per l’arbitrarietà della scelta di CD, AB è la
corda di lunghezza minima
Per definizione
In quanto è il centro della circonferenza inscritta
Un qualsiasi punto Q appartenete alla retta OP può essere preso come centro della circonferenza di
raggio QP e quindi risulta tangente internamente o esternamente alla circonferenza data. Viceversa se
Q è il centro di una circonferenza tangente alla circonferenza data, allora dovrà essere o
OQ ≅ OP + QP , se la tangenza è esterna, oppure OQ ≅ OP − QP , se la tangenza è interna; in ogni
caso O, P e Q risultano allineati
ˆ ≅ APB
ˆ .
Essendo AB ≅ AP , il triangolo PAB è isoscele, quindi ABP
ˆ sono angoli alla circonferenza che
ˆ e PAQ
D’altra parte, ABP
insistono sullo stesso arco AQ, e di conseguenza sono congruenti.
ˆ ≅ APQ
ˆ e quindi il triangolo APQ è isoscele.
Quindi in definitiva PAQ
Sapendo che l’arco PSQ è quattro volte l’arco PTQ , possiamo dedurre che
ˆ
ˆ
ˆ
POQ
PSQ ≅ 4 POQPTQ ⇒ POQPTQ ≅ 360° : 5 ≅ 72° ; quindi
ˆ − POQ
ˆ
ˆ ≅ 360° − OPR
ˆ − OQR
PRQ
≅ 360° − 90° − 90° − 72° ≅ 108°
PTQ
12.
B
A: Vera – Per definizione
B: Falsa – incentro punto di intersezione delle bisettrici
C: Vera – per definizione
D: Vera – lo’incentro esiste sicuramente
E: il circocentro esiste sempre
13.
D
14.
C
15.
E
16.
D
17.
C
18.
C
19.
E
20.
B
I) Falsa: solo se ha gli angoli opposti supplementari
II) Vera: teorema
III) Falsa: solo se il rettangolo è un quadrato
IV) Falsa: : solo se ha gli angoli opposti supplementari e la base maggiore congruente al diametro
A: Falsa – l’incentro è sempre interno, l’ortocentro è
sempre il vertice dell’angolo retto
B: Falsa – gli angoli opposti ai cateti sono angoli alla
circonferenza le cui bisettrici bisecano l’arco su cui
insistono solo se passano dal centro della circonferenza
C: Falsa – l’incentro no (v. figura)
D: Falsa – è sempre interno per tutti i triangoli
E: Vera – il circocentro è il punto medio dell’ipotenusa e
l’ortocentro è il vertice dell’angolo retto
A: Falsa – solo se non allineati
B: Falsa – sono infinite
C: Falsa – appartengono all’asse del segmento AB
D: Vera: essendo l’asse il luogo geometrico dei punti del piano equidistanti dagli estremi del
segmento
E: Falsa – per definizione
Deve avere gli angoli opposti sicuramente supplementari
A: Vera – raggi di una stessa circonferenza
B: Vera – teorema delle tangenti
C: Falsa – il quadrilatero ABCD è inscritto e questa è la proprietà di circoscrittibilità dei quadrilateri
D: Vera – teorema delle tangenti
E: Vera – teorema delle tangenti
Per dimostrare che il baricentro divide le mediane in due parti che sono una il doppia dell’altra
c)
ˆ = 90° + β e dunque ACB
ˆ = 90° − 2 β . Poichè il
ˆ = β , CAB
Prima soluzione: Per ipotesi sappiamo che CBA
ˆ ≅ OBC
ˆ . Poiché il triangolo OAB è isoscele si ha che
triangolo OCB è isoscele si ha che OCB
ˆ ≅ OBA
ˆ . Infine, poichè il triangolo OCA è isoscele si ha che
ˆ ≅ β + OBC
ˆ ≅ β + OCB
OAB
(
)
ˆ ≅ OAC
ˆ ≅ CAB
ˆ − OAB
ˆ ≅ ( 90° + β ) − β + OCB
ˆ ≅ 90° − OCB
ˆ . D'altra parte
OCA
ˆ ≅ OCB
ˆ + ACB
ˆ ≅ OCB
ˆ + 90° − 2 β . Dal confronto di queste ultime due formule segue che OCB
ˆ ≅β, e
OCA
quindi OC è parallelo ad HB (angoli alterni interni uguali rispetto alla trasversale CB). Inoltre essendo OAB
isoscele ed M il punto medio della base AB, OM è altezza e quindi perpendicolare ad AB e quindi parallelo a
CH. Quindi OCHM è un rettangolo e quindi i lati opposti HM e OC sono congruenti.
Seconda Soluzione: La retta per A normale a AB incontra la circonferenza circoscritta al triangolo ABC in un
ˆ ≅ ABC
ˆ , in quanto angoli alla circonferenza che insistono sulla stessa corda AC.
(altro) punto K per cui AKC
ˆ ≅ BAC
ˆ − KAB
ˆ ≅ BAC
ˆ − 90° ≅ ( per ipotesi ) ABC
ˆ ≅ ABC
ˆ + 90° − 90° ≅ ABC
ˆ . Quindi CAK
ˆ ≅ AKC
ˆ ,
Inoltre CAK
quindi il triangolo AKC è isoscele. Allora l'asse di AK è parallelo a AB, passa per C e per il centro O e dunque
HMOC è un rettangolo e HM ≅ OC.