Con la collaborazione dell’alunno Fabio D’Elia della classe IV sez. A
Indirizzo Informatica Sperimentazione ABACUS
Dell’Istituto Tecnico Industriale Statele A. Monaco di Cosenza
Anno scolastico 2009-2010
Prof. Giancarlo Fionda
Insegnante di Elettronica
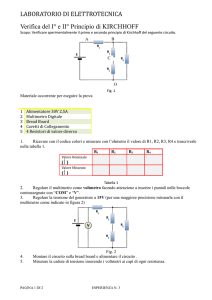
VERIFICA DEI PRINCIPI DI KIRCHHOFF, DEL TEOREMA DI MILLMAN , DEI
TEOREMI DI THÈVENIN E DI NORTON.
La verifica consiste nel misurare le tensioni e le correnti nel circuito; misurare la tensione VAB = V3,
misurare i parametri dei generatori equivalenti di tensione e di corrente.
Schema del circuito
Sigle e valori dei componenti
E1 = E2 = 6V ; R1 = 1,5kΩ ; R2 = 1,8kΩ ; R3 = 2,2kΩ
Apparecchiature e strumentazione
Due alimentatori stabilizzati a tensione variabile; un multimetro digitale 4 ½ digit.
Calcolo dei valori da misurare
Risoluzione del circuito applicando i due principi di Kirchhoff
E1 = E2 = 6V
R1 = 1,5kΩ ; R2 = 1,8kΩ ;
R3 = 2,2kΩ
1
Si scrive una equazione ai nodi e due equazioni alle maglie:
⎧I 3 = I 1 + I 2
⎪
⎨E 1 = R 1 I 1 + R 3 I 3
⎪E = R I + R I
3 2
3 3
⎩ 2
⎧I 3 = I 1 + I 2
⎪
⇒ ⎨R 1 I1 + R 3 (I1 + I 2 ) = E 1
⎪R I + R (I + I ) = E
3 1
2
2
⎩ 3 2
⎧(R 1 + R 3 )I1 + R 3 I 2 = E 1
⇒ ⎨
⎩R 3 I1 + (R 3 + R 3 )I 2 = E 2
⎧I 3 = I 1 + I 2
⎪
⇒ ⎨R 1 I 1 + R 3 I 1 + R 3 I 2 = E 1
⎪R I + R I + R I = E
3 1
3 2
2
⎩ 3 2
⇒
⎧⎪3,7 ⋅ 10 3 I1 + 2,2 ⋅ 10 3 I 2 = 6
⇒ ⎨
⎪⎩2,2 ⋅ 10 3 I1 + 4 ⋅ 10 3 I 2 = 6
Sottraendo membro a membro, si ha:
⎧⎪3,7 ⋅ 10 3 I1 + 2,2 ⋅ 10 3 I 2 = 6
⎨
3
3
⎪⎩2,2 ⋅ 10 I1 + 4 ⋅ 10 I 2 = 6
1,5 ⋅ 10 3 I1 − 1,8 ⋅ 10 3 I 2 = 0I1 =
1,8
⋅ I 2 = 1,2 ⋅ I 2
1,5
Si sostituisce nella seconda e si calcola I2 e, quindi, I1:
2,2 ⋅ 10 3 ⋅ 1,2I 2 + 4 ⋅ 10 3 I 2 = 6 ⇒ 6,64 ⋅ 10 3 I 2 = 6 ⇒ I 2 =
I1 = 1,2I 2 = 1,2 ⋅ 0,903 ⋅ 10 −3 = 1,084mA
I 3 = I1 + I 2 = 1,084 ⋅ 10 −3 + 0,903 ⋅ 10 −3 = 1,987mA
;
V1 = R 1 I1 = 1,5 ⋅ 10 3 ⋅ 1,084 ⋅ 10 −3 = 1,626V
6
= 0,903mA
6,64 ⋅ 10 3
V2 = R 2 I 2 = 1,8 ⋅ 10 3 ⋅ 0,903 ⋅ 10 −3 = 1,6254V
;
V3 = R 3 I 3 = 2,2 ⋅ 10 3 ⋅ 1,987 ⋅ 10 −3 = 4,3714V
Risoluzione del circuito applicando il teorema di Millman tra i nodi A e B
VAB
E1 E 2
6
6
+
+
3
R1 R 2
7,33
1,5 ⋅ 10 1,8 ⋅ 10 3
=
=
=
= 4,3734V
1
1
1
1
1
1
1,6767
+
+
+
+
R 1 R 2 R 3 1,5 ⋅ 10 3 1,8 ⋅ 10 3 2,2 ⋅ 10 3
2
Determinazione dei generatori equivalenti di Thevenin e di Norton
Calco di Eo
E1 E 2
6
6
+
+
3
R
R 2 1,5 ⋅ 10 1,8 ⋅ 10 3
Eo = 1
=
= 6V
1
1
1
1
+
+
R 1 R 2 1,5 ⋅ 10 3 1,8 ⋅ 10 3
Calcolo di Io
Io =
E1 E 2
6
6
+
=
+
= 7,33mA
3
R 1 R 2 1,5 ⋅ 10 1,8 ⋅ 10 3
Calcolo di Ro
R 1R 2
1,5 ⋅ 10 3 ⋅ 1,8 ⋅ 10 3
Ro =
=
= 0,82kΩ
R 1 + R 2 1,5 ⋅ 10 3 + 1,8 ⋅ 10 3
3
Procedimento
1.
2.
3.
4.
Si misurano le resistenze;
Si monta il circuito e si collegano i generatori regolati a 6V;
Si misurano le differenze di potenziale ai capi delle resistenze: V1, V2, V3;
Utilizzando i valori di tensione e di resistenza misurati, si calcolano, applicando la legge di Ohm
ai capi delle resistenze, i valori delle correnti: I1, I2, I3;
5. Si toglie dal circuito la resistenza R3 e si misura, utilizzando il multimetro una volta come
voltmetro e una volta come amperometro, la tensione a vuoto Eo e la corrente di corto circuito Io
tra i punti A e B;
6. Si scollegano i generatori e al loro posto si inseriscono due fili di collegamento e si misura,
utilizzando il multimetro come Ohmmetro, la resistenza Ro vista tra i punti A e B.
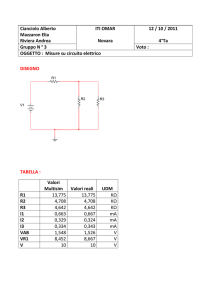
7. Si tabulano i valori misurati e quelli calcolati , per una migliore e più immediata interpretazione
dei dati.
Volt
kΩ
Volt
R3
V1
V2
mA
V3
I1
I2
I3
Volt
mA
kΩ
Eo
Io
Ro
E1 = E2
R1
R2
Valori misurati
6
1,49
1,76
2,18 1,626 1,626 4,395 1,089 0,922 2,014
6
7,4
0,806
Valori calcolati
6
1,5
1,8
2,2
6
7,33
0,82
1,626 1,625 4,371 1,084 0,903 1,987
Considerazioni
I valori misurati sono in ottimo accordo con quelli calcolati.
4