1
STATI DI AGGREGAZIONE DELLA MATERIA
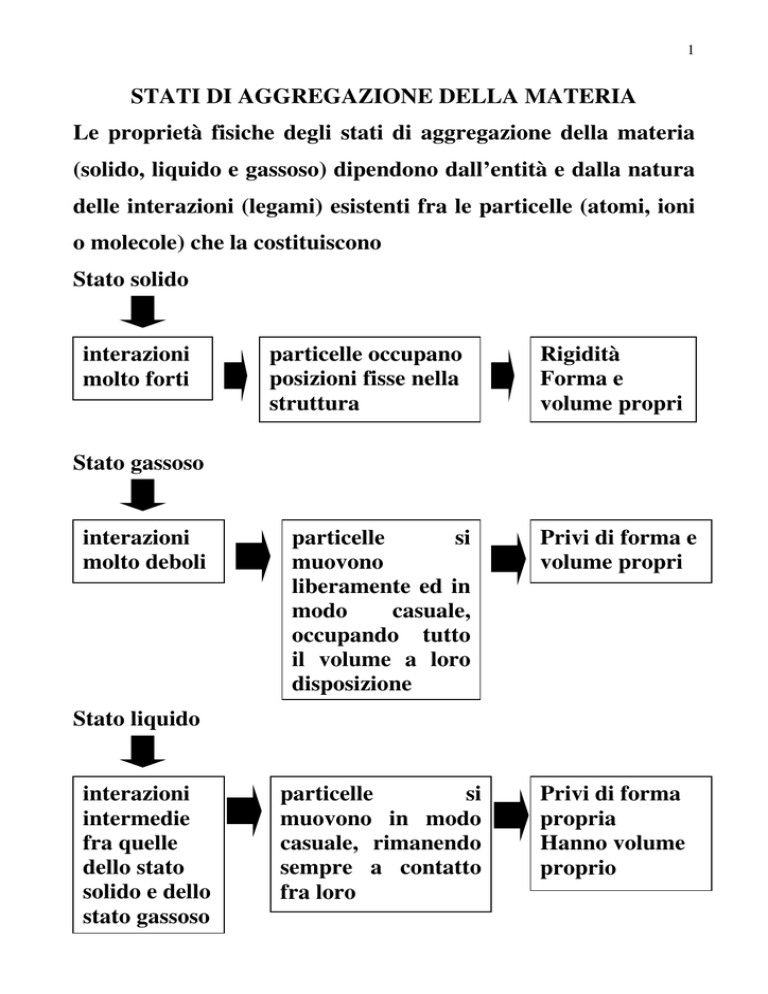
Le proprietà fisiche degli stati di aggregazione della materia
(solido, liquido e gassoso) dipendono dall’entità e dalla natura
delle interazioni (legami) esistenti fra le particelle (atomi, ioni
o molecole) che la costituiscono
Stato solido
interazioni
molto forti
particelle occupano
posizioni fisse nella
struttura
Rigidità
Forma e
volume propri
Stato gassoso
interazioni
molto deboli
particelle
si
muovono
liberamente ed in
modo
casuale,
occupando tutto
il volume a loro
disposizione
Privi di forma e
volume propri
particelle
si
muovono in modo
casuale, rimanendo
sempre a contatto
fra loro
Privi di forma
propria
Hanno volume
proprio
Stato liquido
interazioni
intermedie
fra quelle
dello stato
solido e dello
stato gassoso
2
I GAS
I gas sono i sistemi chimici più semplici e le loro condizioni
sono descritte sulla base di quattro grandezze:
numero di moli (quantità di materia)
grandezze estensive
volume
pressione
grandezze intensive
temperatura
Bassa pressione
Alta
temperatura
Gas ideale:
Interazioni
fra
le
particelle
trascurabili
Il comportamento è
uniforme,
indipendentemente
dalla natura del gas
considerato
modello di gas che permette di descrivere
efficacemente il comportamento dei gas ad alte
temperature e basse pressioni, utilizzando
alcune leggi semplici ed esatte
Il comportamento dei gas reali si allontana da quello del gas
ideale al crescere della pressione e al diminuire della
temperatura, cioè al crescere delle interazioni fra le particelle
gassose
3
Il comportamento del gas ideale è descritto da quattro leggi:
Legge di Boyle (isoterma)
(P⋅⋅V)T = cost
Legge di Charles (isobara)
(V/T)P = cost
Legge di gay-Lussac (isocora)
(P/T)V = cost
Legge di Avogadro
V ∝ n (P, T costanti)
4
Dalla combinazione delle leggi dei gas ideali si ottiene la Legge
di Stato dei Gas Ideali
P⋅⋅V = n⋅⋅R⋅⋅T
P = pressione
V = volume
n = numero di moli
T = temperatura assoluta (K)
R = costante universale dei gas
(8.31 J K-1 mol-1)
Questa equazione descrive il comportamento di un gas ideale
in qualsiasi condizione di temperatura e pressione
Quando il comportamento di un gas reale è descritto Legge di
Stato dei Gas Ideali, esso si comporta come un gas ideale
5
MISCELE DI GAS
La pressione totale esercitata da una miscela di due o più gas,
che si comportino idealmente e non reagiscano fra loro, è
determinata dal numero totale di molecole (di moli)
Gas 1
n1
Ptot = ntot ⋅
P1 = n1 ⋅
R ⋅T
V
Gas 2
n2
Gas 3
n3
R⋅T
R ⋅T
= (n1 + n2 + n3 ) ⋅
V
V
P2 = n2 ⋅
Ptot = P1 + P2 + P3 = ∑ Pi
R ⋅T
V
P3 = n3 ⋅
R ⋅T
V
Legge di Dalton
i
La pressione esercitata da una miscela di gas è pari alla
somma
delle
pressioni
che
ciascun
gas
componente
eserciterebbe se occupasse da solo tutto il volume, alla stessa
temperatura (pressioni parziali)
6
SOLUZIONI
Una soluzione è un sistema omogeneo costituito da almeno due
sostanze, le cui quantità relative possono variare con
continuità entro un certo intervallo, più o meno ampio
Solvente: sostanza presente in quantità maggiore
Soluto: sostanza presente in quantità minore
Una soluzione si ottiene dalla dissoluzione di uno o più soluti
in un solvente. In generale:
Solvente: sostanza allo stato liquido
Soluto: sostanza solida, liquida o gassosa
Per definire le proprietà di una soluzione è necessario
conoscere:
1)
la natura delle sostanze che la compongono
2)
le quantità relative delle sostanze che la compongono
La quantità relativa di un soluto disciolto in un solvente è
detta concentrazione del soluto nella soluzione e può essere
espressa in vari modi
7
CONCENTRAZIONE DELLE SOLUZIONI
Può essere espressa in vari modi
1) Percentuale in peso (% p/p): grammi di soluto presenti in
100 grammi di soluzione
2) Percentuale in peso su volume (% p/V): grammi di soluto
presenti in 100 cm3 di soluzione
3) Percentuale in volume (% V/V): cm3 di soluto presenti in
100 cm3 di soluzione
4) Parti per milione (ppm):
grammi di soluto in 1 tonnellata (106 gr) di soluzione
mg di soluto in 1 Kg di soluzione
5) Molarità (M): numero di moli di soluto disciolte in 1 dm3
di soluzione (mol/dm3)
6) Molalità (m): numero di moli di soluto disciolte in 1 Kg di
solvente (mol/Kg)
7) Normalità (N): numero di equivalenti di soluto disciolte in
1 dm3 di soluzione (eq/dm3)
8) Frazione Molare: rapporto fra il numero di moli di un
componente della soluzione ed il numero di moli totali
χ=
ni
n
= i
ntot ∑ ni
i
ni= numero di moli dell’iesimo
componente
∑ ni = numero di moli totali
i
8
PRORPRIETÀ COLLIGATIVE DELLE SOLUZIONI
Dipendono esclusivamente dal numero di particelle presenti e
non dalla loro natura
Gas
Soluzioni
Pressione
Volume
Abbassamento della tensione di vapore
Abbassamento crioscopico
Innalzamento ebullioscopio
Pressione osmotica
Le leggi che descrivono le proprietà colligative delle soluzioni
sono valide solamente per soluzioni molto diluite, che si
comportano in modo ideale
9
TENSIONE DI VAPORE
ve >> vc
ne >> nc
liq vap
ve > vc
ne > nc
liq vap
ve = vc
ne = nc
liq vap equilibrio
La pressione esercitata dal vapore in equilibrio col liquido è
detta tensione di vapore del liquido. Essa è indipendente dalla
quantità di sostanza considerata, dalla sua superficie e dal
volume del vapore. La tensione si vapore dipende dalla
temperatura e dalle proprietà chimiche della sostanza
considerata. Un liquido si dice volatile quando è caratterizzato
da una elevata tensione di vapore
10
La tensione di vapore del solvente in una soluzione è data da
Psolv = χsolv ⋅Psolv (puro)
Poiché la frazione molare del solvente nella soluzione è
necessariamente minore di 1 (χsolv < 1), ne consegue che
la tensione di vapore del solvente in una soluzione è inferiore
rispetto alla tensione di vapore del solvente puro
L’abbassamento della tensione di vapore del solvente in una
soluzione rispetto al solvente puro dipende solamente dal
numero relativo di particelle nella soluzione e non dalla loro
natura chimica
11
INNALZAMENTO EBULLIOSCOPICO
La temperatura di ebollizione di un liquido corrisponde alla
temperatura alla quale la sua tensione di vapore è pari alla
pressione esterna. La temperatura di ebollizione del solvente
in una soluzione è sempre superiore a quella del solvente puro.
L’innalzamento
ebullioscopico
è
la
differenza
fra
le
temperature di ebollizione del solvente nella soluzione e del
solvente puro (∆Teb)
∆Teb = Keb⋅m
Keb costante ebullioscopica del solvente
m molalità della soluzione
ABBASSAMENTO CRIOSCOPICO
La temperatura di solidificazione di un liquido corrisponde
alla temperatura alla quale la tensione di vapore del liquido e
del solido coincidono.
La temperatura di solidificazione del solvente in una soluzione
è sempre inferiore a quella del solvente puro. L’abbassamento
crioscopico è la differenza fra le temperature di solidificazione
del solvente nella soluzione e del solvente puro (∆Tcr)
∆Tcr = Kcr⋅m
Kcr costante crioscopica del solvente
m molalità della soluzione
L’innalzamento ebullioscopio e l’abbassamento crioscopico
dipendono solamente dal numero di particelle di soluto
presenti in soluzione e non dalla loro natura chimica
12
PRESSIONE OSMOTICA
A: solvente puro
B: soluzione
Membrana
semipermeabile
Si verifica il passaggio di molecole di solvente dal solvente
puro (A) alla soluzione (B), fino a quando la pressione
esercitata dalla colonna di liquido di altezza h è tale da opporsi
all’ulteriore passaggio di molecole di solvente da A a B.
Lo stesso fenomeno si verifica anche quando si mettono a
contatto due soluzioni a differente concentrazione. In questo
caso, il solvente passa dalla soluzione più concentrata a quella
più diluita.
13
La pressione che deve essere esercitata sulla superficie della
soluzione per impedire il passaggio di molecole di solvente
nella soluzione è detta pressione osmotica
Π⋅V = n⋅R⋅T
Π = pressione osmotica
V = volume
n = numero di moli
T = temperatura assoluta (K)
R = costante universale dei gas
(8.31 J K-1 mol-1)
La pressione osmotica di una soluzione dipende solamente dal
numero di particelle di soluto presenti in soluzione e non dalla
loro natura chimica
14
REAZIONI CHIMICHE E STECHIOMETRIA
Reazione chimica: trasformazione nel corso della quale alcune
sostanze (reagenti) si trasformano in altre
(prodotti), in seguito alla rottura e alla
formazione di legami chimici
Nel corso di una reazione chimica non si formano e non si
distruggono atomi, cambiano solamente i legami che li tengono
uniti
Le razioni chimiche sono rappresentate simbolicamente e
sinteticamente per mezzo di equazioni chimiche del tipo
reagenti → prodotti
→ : reagiscono per dare, formano
Reagenti e prodotti sono rappresentati mediante le rispettive
formula chimiche, le quali hanno il significato quantitativo di
1
molecola
o
aggregato
di
atomi
(ragionando
microscopicamente, di 1 mole di sostanza)
Nell’equazione, reagenti e prodotti sono preceduti da un
numero, detto coefficiente stechiometrico, che specifica il
numero di molecole (o di moli) di sostanza che partecipano
alla reazione, definendo i rapporti quantitativi secondo cui i
reagenti si combinano e i prodotti si formano
15
a)
(1) C + (1) O2 → (1) CO2
combustione di C
A livello microscopico:
- 1 atomo di C reagisce con 1 molecola di O2 per dare 1
molecola di CO2
A livello macroscopico:
- 1 mole di (atomi di) C reagisce con 1 mole di (molecole
di) O2 per dare 1 mole di (molecole di) CO2
Ricordando le masse molari di reagenti e prodotti si ha che:
12.01 g di C reagiscono con 32 g di O2 per dare 44.01 g di CO2
NB:
Per convenzione, il coefficiente stechiometrico 1 va
omesso
C + O2 → CO2
b)
H2 + Cl2 → 2 HCl
A livello microscopico:
- 1 molecola di H2 reagisce con 1 molecola di Cl2 per dare 2
molecole di HCl
A livello macroscopico:
- 1 mole di (molecole di) H2 reagisce con 1 mole di (molecole
di) Cl2 per dare 2 moli di (molecole di) HCl
16
c)
2 Na + Cl2 → 2 NaCl
A livello microscopico:
- 2 atomi di Na reagiscono con 1 molecola di Cl2 per dare 2
unità formula di NaCl
A livello macroscopico:
- 2 mole di (atomi di) Na reagiscono con 1 mole di
(molecole di) Cl2 per dare 2 moli di NaCl
Poiché nel corso di una reazione avviene una ricombinazione
degli atomi dei reagenti per formare i prodotti, tutti gli atomi
che costituiscono i reagenti devono ritrovarsi nei prodotti,
anche se combinati diversamente
Principio di conservazione della materia: la massa di ciascun
elemento all’inizio della reazione è uguale a quella della fine
della reazione stessa
Per bilanciamento di una reazione si intende la correzione dei
coefficienti stechiometrici allo scopo di soddisfare al principio
di conservazione della materia
Una reazione è bilanciata quando il numero di atomi di
ciascun elemento nei reagenti e nei prodotti è lo stesso
17
Un’equazione chimica deve descrivere fedelmente il processo
chimico reale. La correttezza di una equazione chimica non
deve perciò essere valutata esclusivamente su basi puramente
algebriche, ma anche facendo riferimento a criteri chimici che
permettano di prevedere correttamente i prodotti finali
Zn° + 2 HCl → Zn(Cl)2 + H2
Equazione formalmente
corretta
Reazione reale
Cu° + 2 HCl → Cu(Cl)2 + H2
Equazione formalmente
corretta
La reazione non avviene
perché è chimicamente
impossibile
18
Nell’equazione chimica devono comparire solamente le specie
chimiche che prendono parte effettiva alla reazione. Perciò:
1)
si trascurano tutte le specie chimiche che, pur essendo
presenti nell’ambiente di reazione, non vi prendono parte
attiva
Gli altri componenti dell’aria
(ad es. N2) sono omessi, perché
non partecipano alla reazione
C + O2 → CO2
Quando le reazioni avvengono in soluzione, il solvente viene
omesso, tranne nel caso in cui venga in parte formato o
consumato nel corso della reazione stessa
2)
Per reazioni in soluzione, è necessario considerare le
eventuali trasformazioni cui le sostanze vanno incontro,
in seguito al processo di solubilizzazione
Sostanze pure insolubili nel solvente considerato sono indicate
con la loro formula chimica
P4
N2
AgCl
CaCO3
Sostanze solubili nel solvente considerato sono indicate con le
specie effettivamente presenti in soluzione, le quali prendono
parte diretta alla reazione, trascurando le altre
19
Ad esempio, mescolando due soluzioni acquose di AgNO3 e
NaCl si ha che
Na+(aq) + Cl-(aq) + Ag+(aq) + NO3-(aq) → Na+(aq) + NO3-(aq)+ AgCl(s)↓↓
Ag+(aq) + Cl-(aq) → AgCl(s)↓↓
La reazione è indipendente
dal tipo di sali solubili di
Ag e Cl utilizzati
Il pedice
aq
indica che gli ioni sono idratati
Il pedice
s
indica che AgCl è presente come solido
(insolubile)
I composti solubili sono rappresentati con le loro formule
chimiche solamente quando essi prendono parte alla reazione
come sostanze pure allo stato solido, cioè come corpo di fondo
della soluzione
Se un composto chimico è presente in soluzione sotto forma di
più specie, esso è rappresentato con la formula di quella
prevalente.
20
BILANCIAMENTO DI UNA REAZIONE
Per bilanciare una reazione è possibile operare solamente sui
coefficienti stechiometrici, senza alterare le formule dei
reagenti e dei prodotti, né introdurre specie chimiche estranee
alla reazione
In generale:
1)
Bilanciare per primo l’elemento che compare nel minor
numero di composti nelle due parti dell’equazione
2)
Bilanciare per ultimo l’elemento che compare come
elemento puro nei reagenti e nei prodotti (qualora sia
presente)
NB: Il bilanciamento è il risultato di un processo razionale e
non la conclusione di tentativi più o meno casuali
21
Na(s) + Cl2(g) → NaCl(s)
la reazione non è bilanciata
Vi sono due possibilità per il bilanciamento
a) da 1 molecola di Cl2
si formano
2 NaCl
e quindi
sono necessari
2 Na
2 Na(s) + Cl2(g) → 2 NaCl(s)
b) da 1 atomo di cloro
½ molecola di
cloro
si forma
1 NaCl
e quindi
è necessario
1 Na
Na(s) + ½ Cl2(g) → NaCl(s)
È possibile usare coefficienti stechiometrici non interi, anche
se, in generale, è preferibile evitarli, dal momento che hanno
significato solo a livello macroscopico (è possibile parlare di
1/2 mole, ma non di ½ molecola). Nel presente caso, abbiamo
che
1 mole di Na(s) reagisce con ½ mole di Cl2(g) per dare 1 mole di
NaCl(s)
22
Na(s) + H2O → Na+(aq) + OH-(aq) + H2(g)
a) 2 molecole
di H2O
non bilanciata
elettroneutralità
1 molecola di H2
2 ioni OH-
2 ioni Na+
2 atomi di Na
2 Na(s) + 2 H2O → 2 Na+(aq) + 2 OH-(aq) + H2(g)
b) 1 mole
di H2O
1/2 mole di H2
1 mole di OH-
elettroneutralità
1 mole di Na
1 mole di Na
Na(s) + H2O → Na+(aq) + OH-(aq) + ½ H2(g)
CH4(g) + O2 (g) → CO2 (g) + H2O (g)
combustione di CH4
non bilanciata
- 4 atomi di idrogeno a sx (CH4) → 4 atomi di idrogeno a dx
2 H 2O
- 1 atomo di C a sx (CH4) → 1 atomo di C a dx (CO2) → OK
CH4(g) + O2 (g) → CO2 (g) + 2 H2O (g)
- 4 atomi di ossigeno a dx → 4 atomi di ossigeno a sx → 2 O2
(CO2+H2O)
CH4(g) + 2 O2 (g) → CO2 (g) + 2 H2O (g)
bilanciata
23
REAZIONI DI EQUILIBRIO
Le reazioni possono essere divise in due grandi gruppi
a) reazioni in cui la conversione dei reagenti nei prodotti è
praticamente totale (reazioni irreversibili)
CH4(g) + 2 O2 (g) → CO2 (g) + 2 H2O (g)
b) reazioni in cui la conversione dei reagenti nei prodotti è
incompleta. In questo caso, i reagenti non scompaiono,
poiché i prodotti reagiscono significativamente fra loro
riformandoli.
In questo caso, si instaura un equilibrio dinamico, nel quale
reagenti e prodotti coesistono in un rapporto quantitativo fisso
nel tempo, caratterizzato dal fatto che il numero di moli di
reagenti che si trasformano nell’unità di tempo nei prodotti è
esattamente uguale a quello delle moli di reagenti che si
formano per reazione dei prodotti
vf
reagenti prodotti
vr
All’equilibrio la velocità della reazione diretta è esattamente
uguale a quella della reazione inversa
24
3 H2(g) + N2 (g) 2 NH3 (g)
Una volta raggiunto l’equilibrio, il
numero di moli di NH3 che si formano
nell’unità di tempo coincide con quello
delle moli che dissociano per dare di
N2 e H2. A causa di ciò, all’equilibrio il
numero di moli di reagenti e prodotti
presenti nell’ambiente di reazione è
costante
2 NH3 (g) 3 H2(g) + N2 (g)
Una volta raggiunto l’equilibrio, il
numero di moli di N2 e H2 che si
formano nell’unità di tempo coincide
con quello delle moli che reagiscono per
dare di NH3. A causa di ciò,
all’equilibrio il numero di moli di
reagenti
e
prodotti
presenti
nell’ambiente di reazione è costante
25
Per una generica reazione di equilibrio
aA+bBcC+dD
le condizioni di equilibrio dipendono dal valore della costante
di equilibrio K
c
d
aC
⋅ aD
K= a b
a A ⋅ aB
a = attività delle specie chimiche
[
C]c ⋅ [D]d
Kc =
[A]a ⋅ [B]b
3 H2(g) + N2 (g) 2 NH3 (g)
[
NH 3 ]2
Kc =
[H 2 ]3 ⋅ [N 2 ]
H2(g) + I2 (g) 2 HI (g)
Kc =
CO(g) + H2O(g) H2 (g) + CO2(g)
Kc =
[HI ]2
[H 2 ]⋅ [I 2 ]
[H 2 ]⋅ [CO 2 ]
[CO]⋅ [H 2O]
26
La quantità di reagenti e prodotti presenti all’equilibrio
dipende dal valore assunto dalla costante di equilibrio K
K>1
l’equilibrio è spostato
[C]c⋅[D]d > [A]a⋅[B]b
verso i prodotti
K<1
l’equilibrio è spostato
[C]c⋅[D]d < [A]a⋅[B]b
verso i reagenti
Per qualsiasi reazione, il valore di K dipende solamente dalla
temperatura
K = f (T)
27
Principio di Le Chatelier-Brown o Legge dell’Equilibrio
Mobile
Qualora si alterino le condizioni di un sistema all’equilibrio
(variando uno qualsiasi dei fattori che ne determinano la
posizione), l’equilibrio si sposta nella direzione che tende a
ripristinare le condizioni iniziali (cioè il sistema reagisce in
modo da minimizzare gli effetti dovuti a tale variazione)
Questo principio vale per qualsiasi equilibrio sia di tipo
chimico, che fisico (ad es. i passaggi di stato) e implica che
a) se aggiungiamo uno dei componenti (reagenti o prodotti) ad
un sistema all’equilibrio, questo tende a consumarli. Se
invece sottraiamo una certa quantità di un componente dal
sistema, questo tende a ripristinarla
28
Consideriamo la seguente reazione
3 H2(g) + N2 (g) 2 NH3 (g)
T = cost
[
NH 3 ]2
K=
[H 2 ]3 ⋅ [N 2 ]
K è costante
Sottraiamo una certa
Numeratore diminuisce
quantità di NH3
Poiché K è costante,
deve
diminuire
il
denominatore, cioè il
sistema consuma H2 e
N2
denominatore diminuisce
L’equilibrio si sposta
numeratore aumenta
verso destra
Lo stesso comportamento si nota qualora si aggiunga una
certa quantità di reagenti nell’ambiente di reazione
29
Consideriamo la seguente reazione
3 H2(g) + N2 (g) 2 NH3 (g)
T = cost
K è costante
aggiungiamo
una
[
NH 3 ]2
K=
[H 2 ]3 ⋅ [N 2 ]
Numeratore aumenta
certa quantità di NH3
Poiché K è costante,
deve
aumentare
il
denominatore, cioè il
sistema produce H2 e
N2, consumando NH3
denominatore aumenta
L’equilibrio si sposta
numeratore diminuisce
verso sinistra
Lo stesso comportamento si nota qualora si sottragga una
certa quantità di reagenti nell’ambiente di reazione
b) qualora reagenti e/o prodotti siano gassosi, anche la
pressione influisce sulla posizione di equilibrio
30
REAZIONI CHIMICHE
Esistono fondamentalmente 4 classi di reazioni chimiche:
a) reazioni acido-base (o di neutralizzazione)
b) reazioni di precipitazione
c) reazioni di ossidoriduzione
d) reazioni di complessazione
Reazioni acido-base
Per Broensted
-un acido è un composto chimico che dissocia liberando
ioni H+
HCl + H2O → H3O+ + Cl-una base è un composto chimico che agisce da accettore
di ioni H+
NH3 + H2O → NH4+ + OHLe reazioni fra un acido e una base sono dette reazioni acidobase (o di neutralizzazione) e portano alla formazione di un
sale
NaOH + HCl → NaCl + H2O
Na+(aq) + OH-(aq) + H+(aq) + Cl-(aq) → Na+(aq) + Cl-(aq) + H2O
Il bilanciamento di questo tipo di reazioni si basa sul fatto che
le cariche di reagenti e prodotti devono essere uguali
31
Acidi e basi forti: in soluzione sono totalmente dissociati
in
HNO3 + H2O → H3O+ + NO3-(aq)
soluzione
esistono
solamente ioni H3O+ e
NO3in
NaOH → Na+(aq) + OH-(aq)
soluzione
esistono
solamente ioni Na+ e OHAcidi e basi deboli: in soluzione sono dissociati in modo
parziale
CH3COOH + H2O H3O+ + CH3COO-(aq)
reazione
di
equilibrio
La posizione dell’equilibrio (cioè quanto prodotto si è
formato) dipende dalla costante di equilibrio K
Ka
[CH COO ]⋅ [H O ]
=
3
−
3
[CH 3COOH]
+
NB: la concentrazione di
H2O non compare, perché
è costante
Ka è detta costante di dissociazione acida o costante acida
La costante acida è una misura della forza di un acido
Equilibrio
totalmente
Acido forte
Ka>>>1
spostato verso i prodotti
Acido totalmente dissociato
Acido debole
Ka<<<1
Equilibrio
totalmente
spostato verso i reagenti
Acido pochissimo dissociato
32
NH3 + H2O NH4+ + OH-(aq)
reazione
di
equilibrio
La forza della base è espressa dal valore di Kb
Kb
[NH ]⋅ [OH ]
=
4
+
−
[NH 3 ]
Kb è detta costante di dissociazione basica o costante basica
Base forte
Ka>>>1
Equilibrio
totalmente
spostato verso i prodotti
base forte
Acido debole
Ka<<<1
Equilibrio
totalmente
spostato verso i reagenti
Base debole
SCALA DI ACIDITÀ DELLE SOLUZIONI
In H2O
+
2 H 2O H 3O
(aq)
-
+ OH (aq)
Reazione
di
autoprotolisi dell’acqua
Keq = [H3O+]⋅⋅[OH-]= Kw = 10-14 a 25°C
La concentrazione
di
H 2O
non
compare, perché è
costante
A 25 °C, il prodotto delle concentrazioni molari degli ioni
H3O+ e OH- in H2O è sempre pari a 10-14
33
Soluzione acida
HCl + H2O → H3O+ + ClPoiché la concentrazione molare di H3O+ ([H3O+]) cresce per
effetto della presenza dell’acido, quella di OH- ([OH-]) deve
diminuire, dato che il loro prodotto è costante
Soluzione basica
NaOH → Na+ + OHPoiché la concentrazione molare di OH- ([OH-]) cresce per
effetto della presenza della base, quella di H3O+ ([H3O+]) deve
diminuire, dato che il loro prodotto è costante
Soluzione neutra
[H3O+]= [OH-]= x
a 25 °C Kw = [H3O+]⋅⋅[OH-]= x⋅⋅x = x2= 10-14
x=[H3O+]= [OH-]= 10-7 mol/l
34
L’acidità e la basicità di una soluzione sono definite sulla base
di una scala logaritmica (pH)
Il pH di una soluzione è dato dal
pH = -log [H3O+]
logaritmo
in
base
10
della
concentrazione molare degli ioni
H3O+ cambiato di segno
Soluzione neutra
[H3O+] = 10-7 mol/l
pH = 7
Soluzione acida
[H3O+] > 10-7 mol/l
pH < 7
Soluzione basica
[H3O+] < 10-7 mol/l
pH > 7
Ricordando che Kw = [H3O+]⋅⋅[OH-]= 10-14
-log Kw = -log 10-14 = -log[H3O+] + (-log[OH-])
14 = pH + pOH
Soluzioni acide
0 < pH < 7
Soluzioni basiche
7 < pH < 14
NB: la variazione di un’unità di pH corrisponde ad una
variazione di [H3O+] pari a una potenza del 10
pH = 3
[H3O+] = 10-3 mol/l
pH = 2
[H3O+] = 10-2 mol/l
35
REAZIONI DI PRECIPITAZIONE
Prevedono la formazione di prodotti insolubili nel solvente di
reazione, i quali si separano come corpo di fondo nel
recipiente di reazione
H2S (g) + 2 Ag+(aq)→ Ag2S(s)↓↓ + 2 H+(aq)
Il bilanciamento è molto semplice e prevede che le cariche di
reagenti e prodotti siano le stesse
Per un sale insolubile, ad esempio Ag2S
Ag2S(s) 2 Ag+(aq) + S2-(aq)
K = [Ag+]2⋅[S2-] = Kps
Prodotto di
solubilità
[Ag2S(s)] = 1, per
convenzione
Qualora il prodotto [Ag+]2⋅[S2-] superi il prodotto di solubilità
(Kps), si verifica la precipitazione di Ag2S, che si separa come
corpo di fondo
Kps >>>> 1
il sale è solubile
Kps <<<< 1
il sale è poco (o pochissimo) solubile
36
REAZIONI DI OSSIDORIDUZIONE
Implicano uno scambio di elettroni fra i reagenti per dare i
prodotti.
Ossidazione: cessione di elettroni
Riduzione: acquisto di elettroni
4 Fe(s) + 3 O2(g)→ 2 Fe2O3
Fe passa da numero di
ossidazione 0 a +3, cedendo
3 elettroni, quindi si ossida
O passa da numero di
ossidazione
0
a
-2,
acquistando 2 elettroni,
quindi si riduce
Fe(s) + S(s)→ FeS(s)
Fe passa da numero di
ossidazione 0 a +2, cedendo
2 elettroni, quindi si ossida
S passa da numero di
ossidazione
0
a
-2,
acquistando 2 elettroni,
quindi si riduce
Fe → Fe2+ + 2 e-
ossidazione
S + 2 e-→ S2-
riduzione
Fe + S→ FeS
ossidoriduzione
37
Dagli esempi visti è evidente che le reazioni di ossidazione e
riduzione devono procedere parallelamente, in quanto la
prima fornisce gli elettroni necessari alla seconda
Il numero di elettroni ceduti dalla specie che si ossida è uguale
a quello degli elettroni acquistati dalla specie che si riduce
(relazione chiave per il bilanciamento delle reazioni di
ossidoriduzione)
È evidente che
1)
la specie che si ossida cede elettroni a quella che si riduce,
perciò agisce da riducente
2)
la specie che si riduce acquista elettroni da quella che si
ossida, perciò agisce da ossidante
Fe(s) + O2(g)→ Fe2O3
Fe → Fe3+ + 3 eO2 + 4 e-→ 2 O2-
Poiché il n° di elettroni ceduti dal
ferro deve coincidere con quello degli
elettroni acquistati dall’ossigeno
(Fe → Fe3+ + 3 e-) x 4
(O2 + 4 e-→ 2 O2-) x 3
4 Fe + 3 O2 + 12 e-→ 2 Fe2O3 + 12 e-
38
Il bilanciamento di reazioni più complesse prevede tre fasi
1)
bilanciamento del n° degli elettroni scambiati
2)
bilanciamento delle cariche di reagenti e prodotti
3)
bilanciamento del n° di atomi di reagenti e prodotti
MnO4-(aq) + Fe2+(aq) + H+(aq)→ Mn2+(aq) + Fe3+(aq) + H2O
1) MnO4- + 5 e- → Mn2+
il Mn passa da +7 a +2, assumendo
5 e- e si riduce
Fe2+ → Fe3++ 1 e-
il Fe passa da +2 a +3, cedendo 1 ee si ossida
MnO4- + 5 e- → Mn2+
(Fe2+ → Fe3++ 1 e-) x 5
MnO4- + 5 Fe2++ 5 e-→Mn2+ + 5 Fe3++ 5 e- bilanciamento di eMnO4-(aq) + 5 Fe2+(aq) + H+(aq)→ Mn2+(aq) + 5 Fe3+(aq) + H2O
2)
reagenti
5⋅⋅(+2) + (-1) + (+1) = +10
prodotti
1⋅⋅(+2) + 5⋅⋅(+3) = +17
Nei reagenti vi è un difetto di cariche rispetto ai prodotti. Per
equilibrare le cariche sono necessari 8 ioni H+
39
MnO4-(aq) + 5 Fe2+(aq) + 8 H+(aq)→ Mn2+(aq) + 5 Fe3+(aq) + H2O
In questo modo
reagenti
5⋅⋅(+2) + (-1) + 8⋅⋅(+1) = +17
prodotti
1⋅⋅(+2) + 5⋅⋅(+3) = +17
3) reagenti: 1 atomo di Mn
prodotti: 1 atomo di Mn
5 atomi di Fe
5 atomi di Fe
4 atomi di O
1 atomi di O
8 atomi di H
2 atomi di H
Nei prodotti vi è un difetto di atomi di ossigeno e idrogeno
rispetto ai reagenti. Tale difetto può essere corretto
aggiungendo il coefficiente stechiometrico 4 davanti ad H2O,
dato che
8 H+ + 4 O2- → 4 H2O
bilanciamento degli atomi
MnO4-(aq) + 5 Fe2+(aq) + 8 H+(aq)→ Mn2+(aq) + 5 Fe3+(aq) + 4 H2O
40
Le proprietà ossidoriduttive di una specie chimica dipendono
dal valore del suo potenziale di riduzione (E), il quale è
direttamente proporzionale alla sua tendenza a ridursi. Ne
consegue che in una reazione di ossidoriduzione, la specie con
E più grande si riduce, mentre quella con E più piccolo si
ossida.
Ogni specie chimica riduce tutte quelle che hanno potenziale
di riduzione superiore al suo (ossidandosi), mentre ossida tutte
quelle
che
hanno
potenziale
di
riduzione
inferiore
(riducendosi)
a) Cu2+(aq)+ 2 e- → Cu°(s)
E
b) 2 H+(aq)+ 2 e- → H2(g)
E
c) Zn2+(aq)+ 2 e- → Zn°(s)
Poiché E
H+
> E
H2
Zn 2 +
E
Cu 2 +
H+
Cu °
H2
Zn 2 +
Zn °
, H+ ha una tendenza a ridursi
Zn °
superiore rispetto a Zn2+, perciò
Zn°(s)+ 2 H+(aq)→ Zn2+(aq) + H2(g)
41
Poiché E
H+
< E
H2
Cu 2 +
, H+ ha una tendenza a ridursi
Cu °
inferiore rispetto a Cu2+, perciò
Cu°(s)+ 2 H+(aq) →
Il potenziale di riduzione è definito dall’equazione di Nernst
E ox
red
= E° ox
red
−
R ⋅ T [red]
ln
[ox]
n⋅F
E°red/ox = potenziale di riduzione in condizioni standard
(298 K, [red] = [ox] = 1 mol dm-3)
[red] = concentrazione molare della forma ridotta
[ox] = concentrazione molare della forma ossidata
n = numero di e- scambiati
T = temperatura assoluta (K)
R = costante universale dei gas
(8.31 J K-1 mol-1)
Il potenziale di riduzione non è una grandezza assoluta, ma
relativa. Per convenzione, si pone uguale a 0 V (Volt) il
potenziale di riduzione standard della coppia
2 H+(aq)+ 2 e- → H2(g)
E °H +
= 0V
H2
Ne consegue che
se E ox
>> 0 V , la specie ox ha un’elevata tendenza a ridursi
red
se E ox
<< 0 V , la specie ox ha una scarsissima tendenza a
red
ridursi
42
4 Fe(s) + 3 O2(g)→ 2 Fe2O3
Fe → Fe3+ + 3 e-
O2 + 4 e → 2 O
E
Fe 3 +
2-
Fe 2 +
si ossida
< EO2
O 2−
si riduce
Fe + S→ FeS
E
Fe → Fe2+ + 2 eS + 2 e-→ S2-
Fe 3 +
< ES
Fe 2 +
si ossida
S2−
si riduce
43
REAZIONI DI COMPLESSAZIONE
Aggiungendo a soluzioni contenti ioni metallici (di transizione)
opportuni reagenti (detti leganti), in grado di cedere ai primi
una coppia elettronica (formando un legame covalente dativo),
si ottengono nuove specie molecolari, detti composti (o
complessi) di coordinazione
Ni2+(aq) + 6 NH3(aq) [Ni(NH3)6]2+(aq)
K=
[Ni(NH 3 )6 ]
[Ni ] ⋅ [NH 3 ]6
2+ 3
Ogni molecola di NH3
cede una coppia di
elettroni allo ione
metallico
costante di equilibrio della
reazione di formazione del
complesso, costante di stabilità
del complesso
HgI2(s) + 2 I-(aq) [HgI4]2-(aq)
K=
[(HgI ) ]
[I ]
4
- 2
2−
costante di equilibrio della
reazione di formazione del
complesso, costante di stabilità
del complesso










