Facoltà di Ingegneria
Prova Scritta di Fisica I - 14 Febbraio 2008
Compito A versione preliminare
Quesito n. 1
A
R
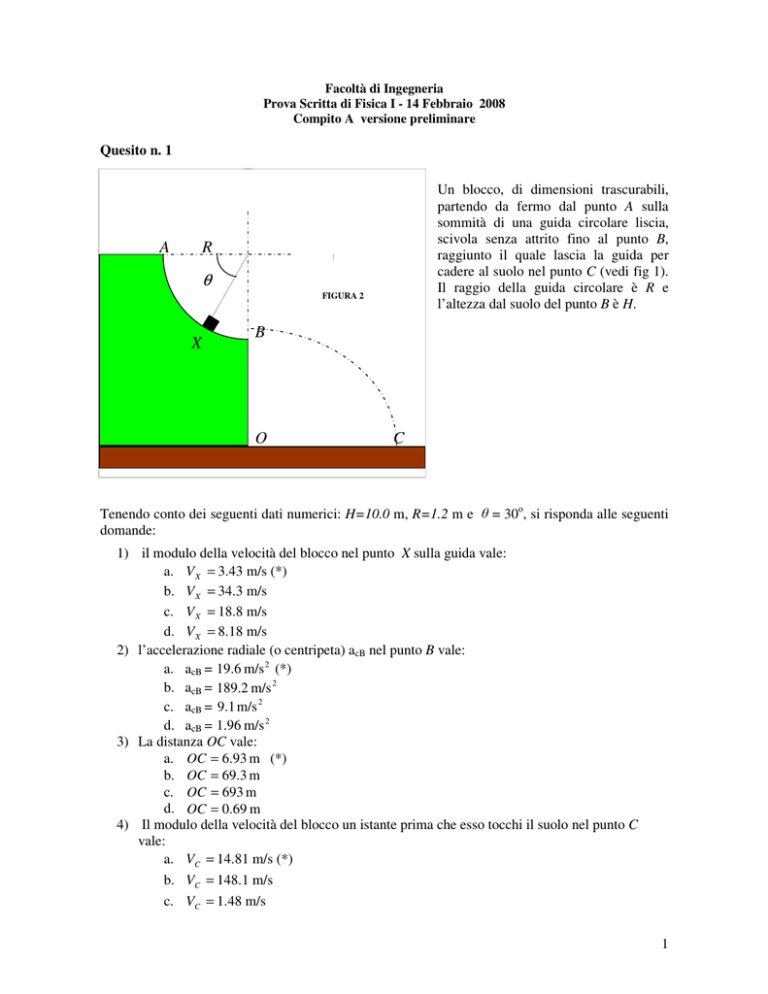
Un blocco, di dimensioni trascurabili,
partendo da fermo dal punto A sulla
sommità di una guida circolare liscia,
scivola senza attrito fino al punto B,
raggiunto il quale lascia la guida per
cadere al suolo nel punto C (vedi fig 1).
Il raggio della guida circolare è R e
l’altezza dal suolo del punto B è H.
D
θ
FIGURA 2
X
B
O
C
Tenendo conto dei seguenti dati numerici: H=10.0 m, R=1.2 m e
domande:
θ
= 30o, si risponda alle seguenti
1) il modulo della velocità del blocco nel punto X sulla guida vale:
a. V X = 3.43 m/s (*)
b. V X = 34.3 m/s
c. V X = 18.8 m/s
d. V X = 8.18 m/s
2) l’accelerazione radiale (o centripeta) acB nel punto B vale:
a. acB = 19.6 m/s 2 (*)
b. acB = 189.2 m/s 2
c. acB = 9.1 m/s 2
d. acB = 1.96 m/s 2
3) La distanza OC vale:
a. OC = 6.93 m (*)
b. OC = 69.3 m
c. OC = 693 m
d. OC = 0.69 m
4) Il modulo della velocità del blocco un istante prima che esso tocchi il suolo nel punto C
vale:
a. VC = 14.81 m/s (*)
b. VC = 148.1 m/s
c. VC = 1.48 m/s
1
5)
d. VC = 0.15 m/s
La componente orizzontale della velocità del blocco nel punto C vale:
a. VC ,orizz = 4.85 m/s (*)
b. VC ,orizz = 48.5 m/s
c. VC ,orizz = 485 m/s
d. VC ,orizz = 0.48 m/s
Quesito n .2
In figura è rappresentata una guida priva di attrito. Al blocchetto di massa m = 1 kg, inizialmente
fermo nel punto A, viene data una spinta tale da farlo partire con velocità appena sufficiente a fargli
percorrere il giro all’interno del tratto circolare della guida, senza perdere il contatto con essa. Il
tratto di guida circolare ha raggio R = 2 m. Il blocchetto prosegue poi il suo moto lungo la guida
fino a fermarsi nel punto C alla quota H. Calcolare il valore di H e rispondere alle seguenti
domande:
6) Nel punto B, sommità del tratto di guida circolare,
C
se il blocco non si stacca dalla guida, il modulo
B
r
della reazione normale N della guida è
H
a. ≥ 0 (*)
b. ≥ mg
c. ≥ 2 mg
d. ≤ 0
(g è l’accelerazione di gravità)
7) Nel punto B, sommità del tratto di guida circolare, il blocco, per non staccarsi dalla guida,
deve avere velocità
a. ≥ Rg (*)
b. ≥ R / g
c. ≥ 3Rg
d. ≥ 2 g / R
8) La velocità che deve essere impressa al blocco in A per fargli percorrere il tratto circolare
della guida, senza staccarsi da essa, è
a. ≥ 1.2 m/s
b. ≥ 5.8 m/s
c. ≥ 8.1 m/s
d. ≥ 9.9 m/s (*)
9) L’energia cinetica Ek(B) del blocco nel punto B, e l’energia potenziale Ep(C) del blocco nel
punto C (rispetto al punto A), sono tali che
a. Ek(B) = Ep(C)
b. Ek(B) ≥ Ep(C)
c. Ek(B) ≤ Ep(C) (*)
d. Ek(B) = Ep(C) / 2
10) Il valore di H, altezza del punto C, vale
a. 3 m
b. 4 m
c. 5 m (*)
2
A
d. 6 m
Quesito n. 3
Una palla di massa m = 0.37 kg viene lanciata verticalmente verso l’alto con velocità iniziale v0 =
14 m/s e raggiunge l’altezza massima H = 8.4 m. Qual è il lavoro compiuto dalla resistenza
dell’aria sulla palla? Supponendo che la resistenza dell’aria compia il medesimo lavoro durante la
discesa , si calcoli la velocità della palla quando ritorna al punto di partenza.
Si risponda quindi alle seguenti domande
11) Il lavoro fatto dall’attrito dell’aria sulla palla nella fase di salita vale
a. – 3.1 J
b. -5.8 J (*)
c. -9.4 J
d. -11.3 J
12) La palla torna a terra con velocità di modulo
a. 1.2 m/s
b. 3.6 m/s
c. 9.1 m/s
d. 11.5 m/s (*)
Quesito n. 4
Nel sistema riportato in figura, si consideri inizialmente la molla non presente:
in tal caso la massa M scende lungo la verticale e trascina un cilindro di massa m e raggio R
lungo il piano inclinato, facendolo rotolare senza strisciare (si consideri il punto O come
punto di contatto tra la massa m e il piano inclinato) . Sapendo che: M = 3 Kg , R = 0.1 m ,
m =1 Kg , β = 30° , H = 80 cm , K =10 N m .
Calcolare:
13) Il modulo dell’accelerazione con cui cade la massa M vale:
m
M − sin β g
2
a. a =
Io
M+
2R 2
(M − m sin β )g
b. a =
M +m
(
M − m cos β )g
c. a =
M + 2m
m
M − sin β g
2
(*)
d. a =
Io
M+
(2 R )2
14) L’accelerazione angolare del cilindro vale:
a. α = 10,90 rad / s 2
M
m
K
O
H
β
b. α = 7 ,42 rad / s 2
c. α = 26 ,61 rad / s 2
d. α = 39,93 rad / s 2 (*)
15) La tensione della fune:
3
Mg
m
a. T = g sin β +
I
2
M + o2
2R
2
Mg 2 R
b. T =
I0
m
M − sin β g
2
(*)
c. T = M g −
Io
M+
2
(2 R )
( M − m sin β ) gR 2
d. T =
3I 0
16) Assumendo che il sistema parta da fermo nella configurazione in cui la massa M dista H dal
suolo, calcolare la velocità angolare del cilindro quando la massa M tocca terra:
a. ω = 17,87 rad s (*)
b. ω = 2 ,12 rad s
c. ω = 4 ,08 rad s
d. ω = 15,16 rad s
Successivamente si consideri nel sistema la molla così come disegnata in figura e si calcoli:
17) L’equazione del moto:
K
(M − m sin β )g
x+
a. a = −
M +m
M +m
m
M − sin β g
K
2
(*)
b. a = −
x+
I
I
M+ o2
2 M + o 2
(2 R )
(2 R )
(M − m cos β )g
K
c. a = −
x+
I
Io
−K
M + o −K
M+
(2 R )
(2 R )
(M − m sin β )g
MK
x+
d. a = −
I
I
M + o2
M + o2
2R
2R
18) la frequenza di oscillazione del sistema:
a. f = 0 ,59 Hz
b. f = 8,15 Hz
c. f = 23,42 Hz
d. f = 0,19 Hz (*)
4
Altre domande
19) Se la risultante di due vettori è nulla, i due vettori
a. sono uguali, ma hanno punto di applicazione diverso
b. hanno modulo e verso uguali, ma direzione diversa
c. hanno modulo e direzione uguali, ma verso opposto (*)
d. hanno verso e direzione uguali, ma modulo diverso
20) L’asse z intorno a cui ruota un corpo rigido è un asse principale di inerzia del corpo. Con
r
r
ovvio significato dei simboli vale la relazione ( P =quantità di moto, L =momento angolare,
r
r
r
M =momento della forza, E c =energia cinetica , ω =velocità angolare, α =accelerazione
angolare)
a.
r
r dL
P=
dt
M = Izω
b.
c. E C = I z α 2
r
r
d. L = I z ω (*)
21) Due ruote uguali A e B hanno la stessa energia cinetica; A sta ruotando intorno ad un asse
fisso passante per il suo CM, B sta invece rotolando (puro rotolamento) su un piano
a. la ruota A ha velocità angolare maggiore di B
b. la ruota B ha velocità angolare maggiore di A
c. le due ruote hanno velocità angolari uguali
d. le due ruote hanno velocità angolari nulle
22) Un blocco scivola su un piano scabro. La forza di attrito compie
a. un lavoro nullo, se il piano è orizzontale
b. un lavoro positivo se il piano è inclinato e il blocco si muove verso il basso
c. un lavoro positivo se il piano è inclinato e il blocco si muove verso l’alto
d. un lavoro negativo, in tutti i casi
23) Dato un sistema di particelle, la variazione della sua energia cinetica è uguale
a. al lavoro delle forze interne
b. al lavoro delle forze esterne
c. al lavoro delle forze interne ed esterne
d. alla variazione dell’energia cinetica del centro di massa
24) In presenza di forze di attrito, l’energia meccanica di un sistema di particelle che evolve da
una configurazione iniziale A ad una configurazione finale B
a. rimane costante (E A = E B )
b. diminuisce (E A > E B ) (*)
c. aumenta (E A < E B )
d. raddoppia (E B = 2E A )
25) Una ruota omogenea ha massa M, raggio R e momento d’inerzia I rispetto all’asse passante
per il suo CM. Se la ruota compie un moto di puro rotolamento, con il CM che si sposta con
velocità di modulo v CM , l’energia cinetica della ruota risulta
a.
b.
c.
d.
1
2
Mv CM
2
1 I 2
1
2
v CM
Mv CM
+
2 R2
2
1 I 2
v CM
2 R2
1
1 2
2
Mv CM
+ Iv CM
2
2
(*)
5
26) Il periodo di oscillazione di un pendolo semplice dipende
a. dall’ampiezza dell’oscillazione
b. dalla quantità di moto
c. dalla massa del pendolo
d. dall’accelerazione di gravità (*)
27) Su due corpi diversi agiscono forze uguali. Si può affermare che le accelerazioni prodotte
sono
a. uguali
b. direttamente proporzionali alle masse
c. direttamente proporzionali al quadrato delle masse
d. inversamente proporzionali alle masse (*)
28) La figura rappresenta due carrucole di raggi r1 ed r2 collegate da una cinghia che non scivola
su di esse. Se la carrucola di raggio r1 ha accelerazione angolare α 1 , l’accelerazione angolare
dell’altra carrucola vale
a. α 2 =
b.
r2
α1
r1
r
α 2 = 1 α1
r2
(*)
c. α 2 =
r1
α1
r1 + r2
d. α 2 =
r1 + r2
α1
r2
r1
r2
r
29) Un disco orizzontale gira intorno al proprio asse con velocità angolare costante ω . Ad un
certo istante un piccolo frammento di massa m cade verticalmente sul disco e si attacca alla
superficie di esso. Il modulo della velocità angolare del disco:
a. raddoppia
b. rimane invariato
c. diminuisce (*)
d. aumenta
30) Un punto materiale si muove di moto rettilineo lungo l’asse x con velocità v = kt con
k=2
m
e t in secondi. Al tempo t = 0 s, il punto materiale si trova nella posizione
s2
x o = x (t = 0 ) = 10m ;
a.
b.
c.
e.
al tempo t =2s il punto materiale si trova nella posizione
x = 8m
x = 10m
x = 12m
x = 14m
Domande di Acustica per Ing. Edile-Architettura
31) Quale e’ sbagliato ?
a. L w = 10 Log( W/ Wo )
b. L I = 10 Log( I / Io )
c. L p = 10 Log( P / Po )
(*)
d. nessuno
32) Al fattore di direttivita’ Q=8 corrisponde una emissione in:
a. un semispazio
b. un quadrante
6
c. un sestante
d. un ottante (*)
33) La formula L p = LW + 10 Log (Q) − 20 Log (r ) − 11 dB e’ valida:
a. in ambiente esterno (*)
b. in ambiente anecoico
c. in ambiente interno
d. e’ sbagliata
34) Nell’acustica architettonica si usa prevalentemente la curva di ponderazione:
a. A
(*)
b. B
c. C
d. D
35) Il tempo di riverbero, secondo Sabine, e’ pari a:
a. T=0.16 Vol / Assorb (*)
b. T=0.16 Assorb / Vol
c. T=0.16 Vol^2 / Riflessione
d. nessuna delle precedenti
4
Q
36) La formula L p = LW + 10 Log (
) e’ valida:
+
2
RL
4π r
a. in ambiente esterno
b. in ambiente anecoico
c. in ambiente interno (*)
d. e’ sbagliata
37) L’intensita’ sonora e’ proporzionale a:
a. pressione
b. quadrato della pressione (*)
c. campo elettrostatico
d. cubo della potenza
38) Per la presenza di componenti tonali in una emissione sonora la normativa prevede una
penalizzazione del livello di pressione di:
a. - 3 dBC
b. +3 dBA (*)
c. +5 dB
d. 0 dBA
39) Le curve isofoniche evidenziano una maggiore sensibilita’ dell’orecchio umano
nell’intervallo:
A. 2-20 Hz
B. 100-500 Hz
C. 2- 5 KHz (*)
D. 15- 20 KHz
40) Ricordando che i valori di riferimento sono: p0 = 20 µPa = 2 × 10-5 Pa, I0 = 10-12 W/m2 ,
quanto vale il livello di intensita’ sonora corrispondente ad una intensita’ di 1 W/m2 ?.
a. 10 dB
b. 100 dB
c. 120 dB (*)
d. 12 dB
Soluzione
Esercizio n. 2
7
r
Nel percorrere la guida il blocco è soggetto alla forza peso mg , sempre diretta verticalmente verso
r
il basso, ed alla reazione vincolare della guida N , diretta radialmente. Nel punto B le due forze
hanno la stessa direzione e lo stesso verso. Affinché il blocco percorra un giro completo senza
perdere il contatto con la guida, occorre dunque che nel punto B l’accelerazione centripeta sia
almeno uguale all’accelerazione di gravità (in tale ipotesi la reazione vincolare della guida nel punto
B risulta nulla), cioè:
v2
m B = mg → v B = gR
R
Applicando il principio di conservazione dell’energia, la velocità che il blocco deve avere in A per
arrivare nel punto B e non staccarsi dalla guida, vale
1 2 1 2
mv = mv B + mg 2 R → v = v B2 + g 4 R = 5 gR = 9.9 m / s
2
2
Dopo aver compiuto il giro nella guida il blocco sale lungo la guida fermandosi nel punto C alla
quota H. Applicando il principio di conservazione dell’energia tra i punti B e C si ha:
v 2 / 2 + 2 gR R
1 2
5
= + 2R = R = 5 m
mv B + mg 2 R = mgH → H = B
2
g
2
2
Esercizio n. 3
Utilizzando il bilancio energetico si ha
1
1
mv 20 + W = mgH quindi Waria = mgH − mv 20 =2
2
4
W
=11.5 m/s
v f = v 02 +
m
5.8 J e, analogamente,
1
1
mv 2C + 2 W = mv f2
2
2
da cui
8