C.d.L. in Ingegneria Meccanica
A.A. 2004-05
Fisica Generale
Prova del 28-09-05
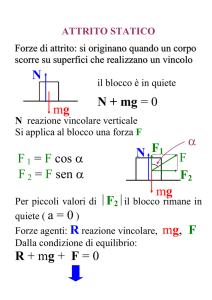
1. Un blocco di massa m = 10.0 kg è lasciato libero
A
in un punto A di una pista ABCD. La guida è
priva di attrito, fatta eccezione per il tratto BC,
6.0m
3.0m
lungo l = 6.0 m . Il blocco scende lungo la guida,
colpisce una molla di costante elastica
D
B
C
k = 2250 N m −1 ,
determinandone
una
compressione ∆x = 0.3 m rispetto alla lunghezza di equilibrio, prima del momentaneo arresto.
Calcolare il coefficiente di attrito dinamico tra blocco e guida nel tratto BC.
Soluzione
Si può calcolare il lavoro della forza di attrito dalla relazione:
LA = ∆E
con ∆E pari alla differenza di energia meccanica tra lo stato finale e.lo stato iniziale.
Nello stato iniziale l’energia è potenziale dovuta alla gravità, mentre nello stato finale è
potenziale elastica. Si ha quindi:
1
1
2
2
LA = k ( ∆x ) − m g h = ( 2250 N m −1 ) ( 0.3 m ) − (10.0 kg ) ( 9.8 m s −2 ) ( 3.0 m ) = −192.75 J
2
2
Il lavoro dell’attrito si calcola da:
G G
LA = FA ⋅ l = − µd m g l
da cui si può calcolare il coefficiente di attrito dinamico:
( −192.75 J )
L
= 0.33
µd = − A = −
mgl
(10.0 kg ) ( 9.8 m s −2 ) ( 6.0 m )
2. Una giostra orizzontale, assimilabile a un cilindro, di massa m = 80 kg e di raggio r = 1.50 m
viene messa in moto, partendo da fermo, da una forza orizzontale costante F = 50 N applicata
tangenzialmente al bordo.
Calcolare l’energia cinetica della giostra dopo un intervallo di tempo ∆t = 3.0 s .
Soluzione
Il momento d’inerzia della giostra è:
1
1
2
I = m r 2 = ( 80 kg )(1.5 m ) = 90 kg m 2
2
2
La forza applicata genera un momento di modulo:
M = F r = ( 50.0 N )(1.5 m ) = 75 N m
a cui compete una accelerazione angolare:
M
75 N m
α=
=
= 0.83 rad s −2
2
I
90 kg m
Dopo il tempo ∆t la velocità angolare è:
ω = α ∆t = ( 0.82 rad s −2 ) ( 3.0 s ) = 2.5 rad s −1
e la corrispondente energia cinetica è:
2
1
1
EK = I ω 2 = ( 90 kg m 2 )( 2.5 rad s −1 ) = 281 J
2
2