UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 05/12/2008
1.
Un proiettile di massa M=10 kg, nel vertice della sua traiettoria
parabolica esplode in due frammenti di massa m1 e m2 che vengono
proiettati nella direzione della tangente alla traiettoria. Sapendo che
nell’esplosione viene liberata una energia E=300J, che la velocità del
proiettile prima dell’esplosione è v=200 m/s, e che il rapporto tra le
masse è m1/m2=3/7, determinare le velocità v1 e v2 dei frammenti.
2.
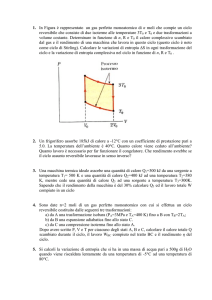
Una mole di un gas ideale avente γ=cp/cv=5/3 partendo dallo stato (pA,
VA, TA) esegue il seguente ciclo reversibile:
(I) una espansione isobara fino al volume VB=5VA,
(II) una trasformazione isocora fino alla pressione pC=(1/3)pA,
(III) una compressione isobara fino al volume VD=VA,
(IV) una trasformazione isocora che riporta il sistema allo stato A.
Si rappresenti il ciclo nel piano pV e si calcoli:
(a) il rendimento del ciclo;
(b) la variazione di entropia del gas e dell’ambiente circostante per
ciascuna delle quattro trasformazioni.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
costante universale dei gas R = 8.314 J/(mole K)
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 28/01/2009
1.
Un blocco di massa m = 200 g viene lasciato libero dalla condizione di
quiete alla quota di h = 0.25 cm su un piano inclinato di un angolo θ =
30° e privo di attrito. Il blocco scende strisciando lungo il piano inclinato,
poi si muove strisciando lungo una superficie orizzontale priva di attrito
finché non urta elasticamente contro un blocco di massa M = 800 g in
quiete ad una distanza di d = 1.4 m dalla base del piano inclinato.
Calcolare:
(a) le velocità dei due blocchi dopo l’urto;
(b) dopo quanto tempo i due blocchi si urtano di nuovo.
p
m
C
A
B
M
h
θ
D
d
2.
V
Una mole di gas perfetto monoatomico esegue il ciclo indicato in figura,
dove AB è una trasformazione isobara, CD isocora, DA e BC
adiabatiche. La temperatura dello stato B è TB = 800 K e il rendimento
del ciclo è del 20%. Sapendo che la variazione di entropia del gas nella
espansione isobara è ∆SAB = 14.6 J/K e che il gas scambia calore solo
con due serbatoi alle temperature TB e TD = 300 K, calcolare:
(c) il lavoro compiuto in un ciclo;
(d) la variazione di entropia totale.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
accelerazione di gravità g = 9.80 m/s2
costante universale dei gas R = 8.314 J/(mole K)
gas monoatomico: calore specifico a volume costante 3 2 R
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 24/02/2009
1.
Un disco di massa 10 kg·e raggio 50 cm ruota con la velocità angolare di
800 giri/min accoppiata al proprio asse (di momento di inerzia
trascurabile). Al medesimo asse viene improvvisamente accoppiato un
secondo disco di pari massa e raggio doppio, inizialmente fermo.
Calcolare:
(a) La velocità angolare del sistema costituito dall’asse e dai due dischi;
(b) La frazione dell’energia cinetica originaria andata perduta.
2.
Una mole di gas perfetto monoatomico, inizialmente alla pressione pA =
1.00 atm e temperatura TA = 500 K, subisce le seguenti trasformazioni:
i)
isoterma reversibile dallo stato iniziale A allo stato B
caratterizzato da VB = 2 VA;
ii)
adiabatica irreversibile dallo stato B allo stato C tale che VC =
3 VB e TC = TA/2;
iii)
isoterma reversibile fino ad un certo stato D caratterizzato da
pD = pA;
iv)
isobara reversibile dallo stato D allo stato iniziale A.
(a) fare un grafico accurato della trasformazione ciclica;
(b) calcolare il rendimento del ciclo realizzato;
(c) calcolare la variazione di entropia del gas nella trasformazione
adiabatica irreversibile.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
Momento di inerzia di un disco rispetto al proprio asse I=½mr2
costante universale dei gas R = 8.314 J/(mole K)
gas monoatomico: calore specifico a volume costante 3 2 R
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 24/04/2009
1.
Un’asta sottile rigida e omogenea di massa m e lunghezza ℓ è vincolata
a ruotare in un piano verticale attorno ad un asse orizzontale passante
per un punto O che dista d = ℓ/3 da un suo estremo; gli attriti sono
trascurabili. L’asta, inizialmente in quiete in posizione orizzontale, viene
lasciata libera di ruotare sotto l’azione della forza peso. Passando per la
posizione verticale essa urta con l’estremo inferiore una massa
puntiforme m1 = m/10 (in quiete e non soggetta a vincoli) che rimane
attaccata all’asta. Calcolare, assumendo ℓ = 1.0 m:
(a) il modulo ω1 della velocità angolare dell’asta immediatamente prima
dell’urto;
(b) il modulo ω2 della velocità angolare dell’asta immediatamente dopo
l’urto;
(c) L’angolo θmax di cui ruota l’asta dopo l’urto prima di invertire il verso
del moto.
2.
Un recipiente contenente del gas perfetto biatomico è diviso da un setto
fisso rigido in due parti A e B di volumi VA e VB = 2 VA. Inizialmente
pressione e temperatura del gas sono tali che pA = 2 pB e TB = 2 TA. Le
pareti esterne del recipiente sono adiabatiche mentre il setto separatore
è permeabile al calore. Si calcoli:
(a) la temperatura TF del gas quando l’equilibrio termico è stato
raggiunto, sapendo che TA = 273 K;
(b) le pressioni p’A e p’B del gas in A e B all’equilibrio, sapendo che
pA = 6.00 atm;
(c) la variazione di entropia dell’universo in corrispondenza al processo
considerato, sapendo che VA = 22.4 ℓ.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
accelerazione di gravità g = 9.80 m/s2
momento di inerzia dell’asta rispetto all’asse ortogonale passante per il centro I=(1/12)mℓ2
costante universale dei gas R = 8.314 J/(mole K)
gas biatomico: calore specifico a volume costante (5/2) R
1 atm = 1.013×105 Pa
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 19/06/2009
1.
Un’asta sottile di massa m1 = 5.0 kg e lunghezza L = 1.0 m, fissa nel suo
estremo A, viene abbandonata da una posizione formante con la
verticale un angolo θ0 = π/3 rad. Essa urta anelasticamente una pallina
puntiforme di massa m2 = 2.0 kg, inizialmente ferma e
tenuta in posizione verticale da un filo inestensibile e di
massa trascurabile, della stessa lunghezza dell’asta,
fissato anch’esso in A. Sapendo che dopo l’urto la
massima elongazione del filo e della pallina è θ2 = 1.0
rad, determinare:
(a) La variazione di energia durante l’urto;
(b) La massima elongazione dell’asta.
2.
Una mole di gas perfetto monoatomico, inizialmente alla pressione p1 =
1.50 atm e temperatura T1 = 300 K, subisce in successione le seguenti
trasformazioni in modo da formare un ciclo reversibile:
i)
una isocora fino alla pressione p2 = 3 p1;
ii)
una isoterma fino alla pressione p3 = 2 p1;
iii)
una adiabatica fino alla pressione p4 = p1;
iv)
una isobara alla pressione p1 fino allo stato iniziale 1.
(a) Determinare tutti i parametri di stato al termine di ciascuna
trasformazione e rappresentare il ciclo su un diagramma pV;
(b) calcolare il rendimento del ciclo e confrontarlo con quello di un ciclo
di Carnot operante tra la massima e la minima temperatura toccata
dal gas;
(c) calcolare la variazione di entropia del gas in ogni trasformazione.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
accelerazione di gravità g = 9.80 m/s2
momento di inerzia di un’asta sottile rispetto all’asse ortogonale passante per il
centro ICM=(1/12)mℓ2
costante universale dei gas R = 8.314 J/(mole K)
gas monoatomico: calore specifico a volume costante = (3/2)R
1 atm = 1.013×105 Pa
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 04/07/2009
1.
Un’asta sottile di massa m1 = 2.0 kg e lunghezza L = 1.0 m, può ruotare
intorno ad un asse orizzontale passante per un punto O distante L/4 da
un estremo dell’asta e sospeso ad un’altezza ¾L da un tavolo
orizzontale. L’asta inizialmente ferma in una posizione formante un
angolo θ0 = π/3 rad con la verticale passante per il centro di sospensione
O, viene lasciata andare e urta elasticamente una massa puntiforme m2
= 0.5 kg, inizialmente ferma poggiata sul tavolo nella posizione
corrispondente alla verticale passante
per il centro di sospensione O e distante
d = 2 m dal bordo del tavolo.
(a) Determinare le velocità di m1 e m2
dopo l’urto.
(b) Sapendo che il coefficiente di attrito
dinamico tra m2 e il tavolo è µd =
0.4 e che il tavolo ha un’altezza h =
0.70 m, determinare la distanza dal
bordo del tavolo alla quale m2 tocca
il suolo.
2.
Una mole di gas perfetto biatomico descrive un ciclo termico costituito
dalle seguenti trasformazioni, tutte reversibili:
i)
una isobara dalla temperatura iniziale T1 = 300 K fino alla
temperatura T2 = 350 K,
ii)
una adiabatica fino alla temperatura T3 = 250 K;
iii)
una isoterma alla temperatura T3 fino al volume iniziale;
iv)
una isocora fino allo stato iniziale.
(a) Rappresentare il ciclo su un diagramma pV.
(b) Calcolare il rendimento del ciclo e confrontarlo con quello di una
macchina di Carnot operante tra la massima e la minima
temperatura toccata dal gas.
(c) Calcolare la variazione di entropia del gas in ogni trasformazione.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
accelerazione di gravità g = 9.80 m/s2
momento di inerzia di un’asta sottile rispetto al centro ICM=(1/12)mℓ2
costante universale dei gas R = 8.314 J/(mole K)
gas biatomico: calore specifico a volume costante = (5/2)R
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 17/07/2009
1.
Su un piano orizzontale liscio, ad una altezza h = 2.0 m dal suolo, sono
poggiati due corpi puntiformi di massa m = 100 g e M = 3 m. Il corpo m
comprime una molla ideale di costante elastica k = 400 N/m, mentre il
corpo M si trova sul bordo del piano (vedi figura). Entrambi i corpi sono
inizialmente fermi. Viene lasciato libero
m che urta elasticamente M facendolo
cadere al suolo nel punto P che dista 50
cm da punto O (vedi figura). Calcolare
(a) la compressione iniziale della
molla;
(b) la distanza da O del punto D in cui
cadrà la massa dopo la ricompressione della molla dopo
l’urto e la successiva ri-espansione.
2.
Una macchina termica, che adopera come sostanza due moli di gas
perfetto biatomico, lavora tra due soli serbatoi T1 e T3 = 3T1. Il gas
esegue un ciclo termico costituito dalle seguenti trasformazioni,:
i)
una compressione isoterma reversibile (1→2) alla temperatura
T1 fino al volume V2 = ½V1;
ii)
una isocora irreversibile (2→3) fino alla temperatura T3;
iii)
una espansione reversibile (3→1), in cui la pressione
diminuisce linearmente all’aumentare del volume, fino allo
stato iniziale.
(a) Rappresentare il ciclo su un diagramma pV e calcolarne il
rendimento.
(b) Calcolare la variazione di entropia del gas nella trasformazione
(3→1).
(c) Calcolare la variazione di entropia dell’universo durante il ciclo.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
accelerazione di gravità g = 9.80 m/s2
costante universale dei gas R = 8.314 J/(mole K)
gas biatomico: calore specifico a volume costante = (5/2)R
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 03/09/2009
1.
Un’asta sottile, di lunghezza L = 1.0 m e massa trascurabile, ha una
estremità incernierata senza attrito ad un sostegno fisso e pende
liberamente nel vuoto. All’estremità libera e nel punto di mezzo dell’asta
ci sono due corpi P1 e P2 (approssimabili a punti materiali) di uguale
massa M1 = M2 = M. Un proiettile di massa m = M/2 urta
perpendicolarmente l’asta nel suo punto di mezzo, con modulo della
velocità v = 10 m/s, e si incastra in P2. Calcolare
(a) la velocità angolare ω0 dell’asta subito dopo l’urto;
(b) di quanto ruota l’asta, rispetto alla posizione iniziale, prima di
fermarsi.
2.
Una macchina termica opera con una mole di gas perfetto monoatomico,
eseguendo un ciclo termico costituito dalle seguenti trasformazioni:
i)
una compressione adiabatica reversibile (A→B),
ii)
una espansione isobara reversibile (B→C),
iii)
una espansione adiabatica irreversibile (C→D),
iv)
una isocora reversibile (D→A).
Sapendo che TA = 300 K, VA = 10.0 ℓ, pB = 10.0 atm, VC = 7.00 ℓ e TD =
750 K:
(a) valutare le coordinate termodinamiche degli stati A, B, C, D e
rappresentare il ciclo su un diagramma pV ;
(b) calcolare il rendimento del ciclo;
(c) calcolare la variazione di entropia dell’universo durante il ciclo.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
accelerazione di gravità g = 9.80 m/s2
costante universale dei gas R = 8.314 J/(mole K)
gas monoatomico: calore specifico a volume costante = (3/2)R
1 atm = 1.013×105 Pa
UNIVERSITÀ DI CATANIA - FACOLTÀ DI INGEGNERIA
D.M.F.C.I.
C.L. INGEGNERIA ELETTRONICA (A-Z)
A.A. 2008/2009
COMPITO DI FISICA SPERIMENTALE I DEL 24/09/2009
1.
Due masse puntiformi, m1 = 180 g e m2 = 20 g, sono fissate agli estremi
di un’asta rigida di massa trascurabile lunga 30 cm. L’asta può ruotare
liberamente in un piano verticale intorno ad un asse orizzzontale di
sospensione che dista 20 cm dalla massa m2 e 10 cm dalla massa m1.
Calcolare:
(a) il periodo delle piccole oscillazioni specificando la posizione di
equilibrio stabile;
(b) la velocità angolare del sistema quando passa per la verticale,
supponendo che esso sia abbandonato con velocità iniziale nulla e
con elongazione angolare iniziale θ0 = 0.1 rad.
2.
Un gas perfetto biatomico, inizialmente alla temperatura T1 = 200 K,
pressione p1 e volume V1, compie una espansione libera fino ad un certo
volume V2. Il gas viene quindi compresso adiabaticamente e
reversibilmente fino ad uno stato (3), in cui la pressione è uguale a
quella iniziale e la temperatura è T3 = 630 K, e infine viene riportato allo
stato iniziale mediante una trasformazione isobara reversibile. Sapendo
che il numero di moli è n = 8, calcolare il lavoro compiuto, il calore
scambiato, la variazione di energia interna e la variazione di entropia in
ciascuna delle trasformazioni e rappresentare schematicamente il ciclo
in un diagramma pV.
⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯⎯≈⎯
Considerare:
accelerazione di gravità g = 9.80 m/s2
costante universale dei gas R = 8.314 J/(mole K)
gas biatomico: calore specifico a volume costante = (5/2)R