LAB

CAMPI DI FORZE CONSERVATIVI
•
PREMESSA
Forza: qualsiasi “causa” in grado di modificare, nella direzione-verso e/o nell'intensità, la velocità di un corpo. La seconda legge della dinamica, o legge di Newton, esprime questa definizione:
F =ma
o meglio:
a=
R
m
dove i simboli a, R, F rappresentano vettori
Questa seconda forma esprime il fatto che
l'accelerazione è l'effetto, mentre R, risultante di tutte le forze applicate, è la causa.
Massa: o inerzia o massa inerziale, è la
tendenza di qualsiasi corpo ad opporsi con
maggiore o minore intensità al cambiamento di velocità.
Campo di forza: si tratta di una “deformazione”, non visibile, dello spazio tridimensionale causata dalla presenza di una
massa (campo gravitazionale) e/o di una carica elettrica (campo elettrico). Il termine
“forza” nel senso di “azione diretta” è obsoleto, superato dalla teoria della relatività.
Una carica “agisce” deformando
lo spazio e qualsiasi altra carica presente in questo spazio modifica la sua
velocità in quanto “segue” la curvatura di questo spazio.
•
Lavoro: si dice lavoro di una forza (costante) che agisce su un corpo durante uno
spostamento il prodotto dello spostamento
per la componente (cioè la proiezione ortogonale) della forza lungo la direzione dello
spostamento. Il lavoro è positivo quando
tale componente è concorde con lo spostamento, negativo nel caso opposto. Se la forza è perpendicolare allo spostamento, il lavoro è nullo.
Se la forza non è costante o lo spostamento non è rettilineo, bisogna immaginare di suddividere la traiettoria
in moltissimi segmenti rettilinei (poligonale), detti “spostamenti infinitesimi”, in ciascuno dei quali si possa ritenere la forza costante. Per ciascuno
di essi si calcola il lavoro e infine si
sommano tutti i lavori. Questa operazione in matematica si chiama “integrale”.
Energia cinetica: l'importanza del lavoro
è espressa dal “teorema” o “legge dell'energia cinetica: il lavoro compiuto su un corpo
durante un certo intervallo di tempo è
uguale alla variazione dell'energia cinetica
del corpo nel medesimo intervallo”
1
1
L t t = m v 21− m v20
2
2
0, 1
CAMPO DI FORZA CONSERVATIVO
Generalmente il lavoro che le forze del campo compiono per spostare una massa (c. gravitazionale) o una carica (c. elettrico) dal punto A al punto B dipende non solo dai punti A e B,
ma anche dal percorso seguito. Questo non succede per tutti i campi di forza.
Il campo gravitazionale e il campo elettrico sono conservativi.
Un campo di forza si dice conservativo quando il lavoro della forza del campo dipende solo dai punti di partenza A e di arrivo B, e non dal percorso seguito:
L AB , = L AB , 
cioè il lavoro da A a B lungo due percorsi qualsiasi, α e β, è uguale.
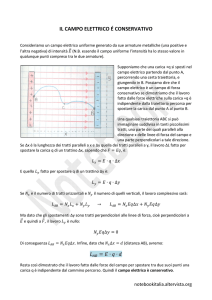
Osservazione 1
Il lavoro di una forza “esterna” per spostare una carica all'interno di un campo elettrico, in
opposizione istante per istante alla forza “interna”, cioè quella del campo stesso, è uguale ed
opposto al lavoro della forza “interna”:
L AB ,est =− L AB ,int
Per esempio, se la gravità compie un lavoro di 100 J per spostare un corpo da una
posizione A ad una posizione B, per effettuare lo stesso spostamento una forza
esterna (potrebbe essere la nostra mano)
compie il lavoro opposto -100 J
Se una carica positiva viene spostata da
un punto lontano ad un punto vicino ad
un'altra carica positiva, la forza elettrica
“interna”, che è di repulsione e quindi opposta allo spostamento, compie un lavoro
NEGATIVO, mentre la forza “esterna” che
noi usiamo per spostare la carica, che è
concorde con lo spostamento, compie lo
stesso lavoro ma POSITIVO.
Osservazione 2
In un campo conservativo, qualunque sia il percorso seguito il lavoro del campo per ritornare dal punto B al punto A è esattamente opposto al lavoro compiuto da A a B.
L BA , =−L AB ,
ritorno lungo lo stesso percorso
L BA , =−L AB , 
ritorno lungo percorso diverso
Questo è evidente se il percorso è lo
stesso al contrario, in quanto punto per
punto la forza è uguale mentre gli spostamenti sono opposti. Ma anche al contrario qualunque percorso da B ad A è
equivalente in termini di lavoro. Pertanto
ritornando da B ad A il lavoro è sempre
opposto a quello compiuto da A a B.
Si ribadisce che il percorso non influenza il lavoro di un campo conservativo; solo i punti estremi sono importanti.
Osservazione 3 (conseguenza della precedente)
Se un percorso è chiuso, cioè parte da A e arriva in A, allora il lavoro (esterno o interno) in
un campo conservativo è nullo.
Immaginiamo un qualsiasi punto intermedio B: il lavoro su tutto il percorso è la
somma del lavoro da A a B più quello da B ad A. Per quanto detto precedentemente questi lavori sono uguali ed opposti e quindi la somma è zero.
L  , chiuso =L AA= L AB L BA= L AB−L AB =0