Document

Statica
!!
Fisica Generale A
!!
!!
5. Statica
http://campus.cib.unibo.it/2425/
Domenico Galli
!!
Digitally signed by Domenico Galli
DN: c=IT, o=INFN, ou=Personal Certificate, l=Bologna,
cn=Domenico Galli
Date: 2009.06.17 15:19:33 +02'00'
June 17, 2009
!!
!!
La retta su cui si dispone la cordicella rappresenta la direzione della
forza, il dinamometro ne misura il modulo.
Il dinamometro è costituito da una molla a elica cilindrica e da una
scala graduata che consente di misurarne l’allungamento.
Cordicella ideale: infinitamente sottile, perfettamente flessibile e
inestensibile.
!!
Molla ideale: massa nulla, segue precisamente la legge di Hooke:
!!
dove k è una costante.
!!
!!
!!
Concetto di forza: nasce dallo “sforzo”
muscolare.
Fisica Generale A. 5. Statica. 3
Domenico Galli
!
F
Forza peso: dovuta all’attrazione gravitazionale, diretta
lungo la verticale, con verso diretto in basso.
Forza elastica: esercitata dalla molla, proporzionale
all’allungamento della molla.
Equilibrio di un sistema di forze applicate a un punto
materiale: risultante nulla.
"!
" !
!
! !
!
Fp + Fe = 0 ! Fp " k #l = 0
"!
"
!
F = !k "l
dinamometro
Equilibrio: si ha quando un corpo soggetto a
forze, inizialmente in quiete rispetto a un
prestabilito SdR, rimane nello stato di quiete.
Dinamometro e forza peso
Definizione operativa (specificazione del procedimento con cui si
effettua la misura): cordicella + dinamometro.
!!
Statica: studio delle forze (che sono causa dei
cambiamenti dello stato di moto) nelle
configurazioni di equilibrio.
Fisica Generale A. 5. Statica. 2
Domenico Galli
Forza
!!
Cinematica: descrizione del moto,
trascurandone le cause.
!!
Raddoppiando il peso (appendendo
due pesetti uguali) raddoppia pure
l’allungamento della molla.
Fisica Generale A. 5. Statica. 4
Domenico Galli
!
Fe
!
Fp
Natura vettoriale delle forze
!!
Si trova sperimentalmente che le forze si sommano
vettorialmente.
!!
Forze interne e forze esterne
!!
In un sistema di punti materiali si definiscono:
!!
Per 3 forze applicate a un punto materiale si ha l’equilibrio se:
!
! !
F3 = ! F1 + F2
(
)
!
F3
! !
! !
" F1 + F2 + F3 = 0
!
F1
!
F2
!!
!!
Forze interne: le forze esercitate da una parte del sistema
su un’altra parte dello stesso sistema.
Forze esterne: le forze esercitate su di una parte del
sistema da parte di corpi non appartenenti al sistema.
Es.:
!!
! !
!
F1 + F2 = ! F3
!!
Per il sistema costituito dalla sola Terra, l’attrazione
gravitazionale esercitata del Sole sulla Terra è una forza
esterna.
Per il sistema costituito da Terra + Sole l’attrazione
gravitazionale esercitata del Sole sulla Terra è una forza
interna.
Fisica Generale A. 5. Statica. 5
Domenico Galli
Equazioni cardinali della statica
!!
Condizione necessaria e sufficiente per l’equilibrio di
un punto materiale è che si annulli la risultante delle
forze ad esso applicate (NB: questo non significa che
non siano presenti forze!).
! !
R =0
!!
Condizione necessaria e sufficiente per l’equilibrio di
un corpo rigido è che si annullino sia la risultante sia il
momento risultante delle forze esterne ad esso
applicate (NB: le forze interne di coesione del corpo
rigido, che mantengono invariate le distanze tra i
punti, non hanno effetto)
!e !
!e !
R ( ) = 0, M ( ) = 0
Fisica Generale A. 5. Statica. 6
Domenico Galli
Baricentro
!!
!!
!!
!!
Corpo rigido: si può idealmente suddividerlo in n parti
sufficientemente piccole rispetto al contesto
considerato, da poter essere considerate puntiformi.
! !
Se il corpo non è troppo esteso (rispetto alla
dimensione della Terra) tali forze sono parallele tra
loro.
L’insieme delle forze peso
è riducibile a una sola
!
forza, la risultante R , detta peso totale del corpo,
applicata nel centro dei vettori paralleli, che in
questo caso prende il nome di baricentro G.
(equazioni cardinali della statica)
Fisica Generale A. 5. Statica. 7
Domenico Galli
!
Ogni parte è soggetta alla forza peso: F1 , F2 ,..., Fn .
Fisica Generale A. 5. Statica. 8
Domenico Galli
!
R
Baricentro (II)
!!
Baricentro (III)
Il baricentro (essendo il centro dei vettori paralleli) è
definito da:
1 n
G!O=
"F P !O
R i=1 i i
Proiettando sugli assi e prendendo O come origine si
hanno le componenti cartesiane:
(
!!
"
1
$ xG =
R
$
1
$
# yG =
R
$
$z = 1
$ G R
%
!!
)
!!
n
!Fx
!!
i i
i=1
n
!F y
i
i
!!
i=1
n
!Fz
i i
i=1
Per un sistema costituito da 2 soli punti materiali, il
baricentro si trova sul segmento che congiunge i 2
punti, a distanza da essi inversamente proporzionale al
loro peso.
Per un sistema di n punti materiali che giacciono su di
una retta, il baricentro si trova sulla medesima retta.
Per un sistema di n punti materiali che giacciono su di
un piano, il baricentro si trova sul medesimo piano.
Se un sistema può essere diviso in più parti, il suo
baricentro coincide col baricentro dei baricentri
parziali.
!
R
Fisica Generale A. 5. Statica. 9
Domenico Galli
Baricentro (IV)
!!
Baricentro (V)
Per un corpo omogeneo (porzioni di ugual volume hanno
ugual peso), suddividendolo in n parti di ugual volume,
sufficientemente piccole rispetto al contesto
considerato, da poter essere considerate puntiformi,
si ha:
n
"
1 n
1 n
1
1 n
x
=
F
x
=
F
x
=
F
x
=
! i i nF ! i nF ! i n ! xi
$ G
R
i=1
i=1
i=1
i=1
$
1 n
$
# yG = ! yi
n i=1
$
n
$z = 1 z
!
$ G n i=1 i
%
1 n
G ! O = " Pi ! O
n i=1
(
Fisica Generale A. 5. Statica. 10
Domenico Galli
)
Fisica Generale A. 5. Statica. 11
Domenico Galli
!!
!!
Se chiamiamo ps il peso specifico, si può scrivere:
p n
1 n
1 n
G!O=
Vi ps Pi ! O = s "Vi Pi ! O = "Vi Pi ! O
"
R i=1
R i=1
V i=1
Se si fa tendere n!", la sommatoria viene sostituita
da un integrale. Per un corpo omogeneo:
1
G ! O = """ P ! O dV
V V
(
(
"
1
$ xG =
V
$
1
$
# yG =
V
$
$z = 1
$ G V
%
)
(
)
!!! x d x d y d z
V
!!! y d x d y d z
V
!!! z d x d y d z
V
Fisica Generale A. 5. Statica. 12
Domenico Galli
)
(
)
Forze vincolari
!!
!!
Forze vincolari (II)
Ogni vincolo impedisce certi movimenti del corpo
considerato e ne consente altri (es.: rotaia treno,
cardine porta, piano su cui è appoggiato un oggetto,
ecc.).
!
Per impedire i movimenti vietati dei corpi, i vincoli
debbono esercitare sui corpi delle forze, dette
forze vincolari o reazioni vincolari.
!!
Se un corpo, appoggiato su un tavolo, rimane in quiete,
allora la risultante e il momento risultante delle forze che
agiscono su di esso sono entrambi nulli. Il corpo è
sicuramente soggetto alla forza peso diretta lungo la
verticale verso il basso. Affinché sia nulla la risultante,
deve essere presente una forza, diretta lungo la
! verticale
!
verso l’alto. Tale forza è la reazione vincolare Rn = ! Fp
!!
!!
Rn
Le forze non vincolari sono dette forze attive.
Le forze vincolari sono a priori sconosciute, in quanto
debbono adeguarsi alle circostanze per neutralizzare
le forze attive che potrebbero causare movimenti
vietati.
!
Fp
!!
!
Rn1
!
Fp1
Fisica Generale A. 5. Statica. 13
Domenico Galli
Le forze di attrito sono forze che si sviluppano sulla
superfici dei corpi, tangenzialmente ad esse,
ostacolandone il movimento.
!!
!!
!!
!!
Attrito interno: si esplica tra i vari strati di un fluido, dovuto alla
viscosità (es.: differente comportamento tra acqua e miele).
Attrito del mezzo: resistenza viscosa (F # v) o resistenza
idraulica (F # v2) a cui è soggetto un corpo in moto entro un fluido
viscoso.
Attrito radente: quando due corpi solidi sono sollecitati a
strisciare l’uno sull’altro, sulle superfici di contatto si sviluppano
forze tangenziali dovute alle asperità e alle forze di adesione
che si esercitano tra le 2 superfici.
Attrito volvente: si osserva in un cilindro che rotola senza
strisciare su di una superficie. Dovuto alle asperità e alla non
perfetta elasticità dei corpi a contatto.
Fisica Generale A. 5. Statica. 15
Domenico Galli
!
Rn2
!
Fp2
!
!
Rn1 > Rn2
Fisica Generale A. 5. Statica. 14
Domenico Galli
Forze di attrito
!!
Lo stesso tavolo esercita reazioni vincolari diverse su due
oggetti di peso diverso appoggiati su di esso.
Attrito radente
!!
!!
Si manifesta allo strisciare di due corpi l’uno
sull’altro.
È causato dalle asperità delle superfici
striscianti (per cui le irregolarità della superficie
più dura scavano solchi sulla superficie più
tenera) e dall’adesione tra le due superfici che
può produrre delle vere micro-saldature nei
punti di contatto.
!!
Particolarmente intensa è l’adesione tra rame e rame e
tra alluminio e alluminio, che tendono facilmente a
“ingranarsi” o “gripparsi”.
Fisica Generale A. 5. Statica. 16
Domenico Galli
!
Rt
!
F
Attrito radente (II)
!!
!!
!!
Attrito radente (III)
Per diminuire l’attrito radente si utilizzano lubrificanti, ovvero
sostanze (olio, grafite, talco, paraffina) che si interpongono tra
le due superfici che strisciano.
!!
Per minimizzare l’attrito, allo scopo di eseguire esperimenti
precisi di dinamica, si utilizza il “cuscino d’aria”, ovvero si
interpone uno strato di aria tra le superfici.
La tecnica del “cuscino d’aria” viene utilizzata
anche in particolari veicoli anfibi per
trasporto passeggeri denominati hovercraft.
Il ghiaccio secco a temperatura
ambiente sublima in anidride
carbonica gassosa che fuoriesce dal
foro inferiore creando una pellicola
di aria che si interpone tra il disco
e la superficie su cui esso appoggia.
Fisica Generale A. 5. Statica. 17
Domenico Galli
Fisica Generale A. 5. Statica. 18
Domenico Galli
Attrito radente (IV)
!!
!!
!!
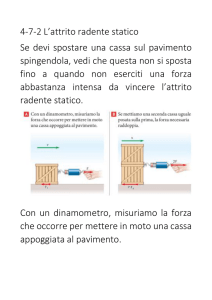
Attrito radente statico
Nello studio dell’attrito radente si distingue tra
attrito statico e attrito dinamico.
!!
!
F <!
Se un corpo pesante appoggia con una faccia su di! un
piano orizzontale e sia applica ad esso una forza F !
diretta orizzontalmente, se il modulo della forza F è
sufficientemente piccolo il corpo non si muove
(attrito statico).
!
Quando invece si aumenta F oltre una certa soglia, il
corpo comincia a muoversi, ma con accelerazione
inferiore a quella che avrebbe in assenza di attrito
(attrito dinamico)
Fisica Generale A. 5. Statica. 19
Domenico Galli
!
Rt
Si osserva sperimentalmente
che esiste un valore di
!
soglia $ del modulo F della forza: il corpo non si
muove se:
!!
Se il corpo non si muove, significa che si trova in
equilibrio statico, dunque la risultante deve essere
nulla:
!
!
! ! !
R = F + Rt(s) = 0 se F < !
!
!
!
Rt(s) = ! F se F < "
!!
!
F
La forza di attrito statico è uguale e opposta alla
forza attiva applicata finché l’intensità F della forza
! (s)
!
si mantiene entro certi limiti.
Fisica Generale A. 5. Statica. 20
Domenico Galli
Rt
F
Attrito radente statico (II)
!!
!!
Attrito radente dinamico
!
Si trova sperimentalmente che:
!
! = f Rn
!
dove Rnè la reazione vincolare della superficie! (forza
d’appoggio), uguale e opposta alla forza peso p. Il
!!
!!
coefficiente adimensionale f è detto coefficiente di
!
attrito statico. Dunque:
!
!
!
!
Rt(s) = ! F se F < f Rn
!
!
Rt(s) " f Rn
!!
!
Rt(s)
f dipende dai materiali di cui sono composte
le superfici e dalla loro scabrosità ed è
approssimativamente indipendente dalla
superficie di appoggio.
Rn
!!
!!
!
p
!
v
!
Rn
Rt
!
F
!
p
Attrito statico e attrito dinamico
!!
!
" ! = µ Rn
!
dove Rn è la reazione vincolare della superficie
! (forza
d’appoggio), uguale e opposta alla forza peso p . Il
!!
coefficiente adimensionale µ è detto coefficiente di
attrito dinamico. Dunque:
!!
!
!
Rt( d ) = µ Rn
Fisica Generale A. 5. Statica. 23
Domenico Galli
Se il corpo non si muove, significa che si
trova in equilibrio statico, dunque la
!(d )
risultante deve essere nulla:
Fisica Generale A. 5. Statica. 22
Domenico Galli
Sperimentalmente si trova inoltre che:
!
v
Si osserva sperimentalmente che il corpo rimane
! in
quiete soltanto per un determinato valore di F :
!
!
! ! !
R = F + Rt( d ) = 0 se F = " !
!
!
!
Rt( d ) = ! F se F = # "
Attrito radente dinamico (II)
!!
Si può studiare staticamente il problema, muovendo il
piano di appoggio e tenendo
fermo il corpo con un
!
opportuno valore di F .
!
F = "!
!
F
Fisica Generale A. 5. Statica. 21
Domenico Galli
!!
Se F ! " il corpo inizia a muoversi.
!
Rt( d )
!
Rn
!
p
!
F
Sperimentalmente risulta sempre:
{
!
!
µ < f ! Rt( d ) < max Rt(s)
}
L’attrito dinamico è sempre minore del limite massimo
dell’attrito statico.
Una semplice esperienza mette in evidenza questa
proprietà: asta appoggiata sui diti indici di due mani. Le
due forze d’appoggio possono essere trovate dalle
equazioni cardinali della statica:
!
!
! ! !
#%R = p + RnA + RnB = 0
!
!
!
!
$ !
M
=
G
!
G
"
p
+
A
!
G
"
R
+
B
!
G
"
R
=
0
nA
nB
!
!
G
&% ( )
(
)
(
)
(
RnA
A
)
RnB
G
a0
Fisica Generale A. 5. Statica. 24
Domenico Galli
!
p
b0
B
Attrito statico e attrito dinamico (II)
!
!
! ! !
#%R = p + RnA + RnB = 0
!
!
$ !
%& M(G ) = A ! G " RnA + B ! G " RnB
!
a0
# RnB = RnA
#
b0
%
"
a
a +b
# p = RnA + 0 RnA = 0 0 RnA
b0
b0
#$
(
!!
!!
)
(
)
Attrito statico e attrito dinamico (III)
#% p = RnA + RnB
$
%& a0 RnA = b0 RnB
!
b0
p
# RnA =
#
a0 + b0
"
a0
# RnB =
p
a0 + b0
#$
!
=0
!!
'
!!
Avviciniamo le dita. Il dito A (forza d’appoggio minore
perché a0>b0) inizia a slittare.
Se fosse µ=f, quando diventa a=b0 (forza d’appoggio
uguale) le due dita inizierebbero
a muoversi insieme.
!
!
RnA
A
a0
Fisica Generale A. 5. Statica. 25
Domenico Galli
!
p
!
RnA
B
b0
Attrito statico e attrito dinamico (IV)
!!
A
a0
!!
A
Fisica Generale A. 5. Statica. 27
Domenico Galli
b0
a1
b1
b0
B
Fisica Generale A. 5. Statica. 26
Domenico Galli
B
Dunque si avrà la successione di punti:
µ
b
f 0
µ
µ2
b1 = a1 = 2 b0
f
f
µ
µ2
µ3
a2 = b1 = 2 a1 = 3 b0
f
f
f
.........................................
!!
!
RnB
a1
!
p
a1 =
}
!
RnA
b0
a1
}
Attrito statico e attrito dinamico (V)
A questo punto l’asta inizia a slittare sul dito B finché
l’attrito dinamico in B diventa uguale al massimo
possibile attrito statico in A.
!
!
!
!
a1
b1
RtB( d ) = max RtA(s) ! µ RnB = f RnA ! µ
= f
a1 + b1
a1 + b1
b1 µ
µ
= < 1 ! b1 = a1 < a1
a1 f
f
{
La distanza a1 in cui A si ferma rispetto all’asta
(mentre B inizia a muoversi) è quella per cui l’attrito
dinamico in A diventa uguale al massimo possibile
attrito
statico
!
! in B:
!
!
b0
a1
RtA( d ) = max RtB(s) ! µ RnA = f RnB ! µ
= f
a1 + b0
a1 + b0
a1 µ
µ
!
= < 1 ! a1 = b0 < b0
RnB
b0
f
f
{
RnB
G
Si osserva invece che il dito A prosegue oltre. Il
motivo è che, quando a=b0 (forze d’appoggio uguali),
l’attrito in A, essendo dinamico è inferiore all’attrito
in B, che è statico.
Si tratta di una progressione geometrica che tende ai
valori limite a = b = 0, corrispondenti al baricentro G.
!
RnA
G RnB
A
!B
p
Fisica Generale A. 5. Statica. 28
Domenico Galli
!
Attrito statico e attrito dinamico (VI)
!!
Attrito volvente
Evidenze pratiche del fatto che l’attrito dinamico è
sempre minore del limite massimo dell’attrito statico:
!!
!!
!!
Quando si sposta, strisciandolo, un mobile pesante, per
metterlo in movimento (cioè per vincere il massimo attrito
statico) occorre imprimergli una forza maggiore di quella
necessaria per mantenerlo in movimento (che serve per
vincere l’attrito dinamico).
!!
!!
Le automobili recenti sono dotate di un dispositivo antipatinamento (ABS). Se la ruota patina, ovvero striscia,
sull’asfalto, la forza di attrito diviene dinamica, e dunque
l’azione frenante risulta inferiore. Il dispositivo ABS, quando
la ruota patina rilascia un po’ il freno, in modo da ripristinare
le condizioni di attrito statico.
Fisica Generale A. 5. Statica. 29
Domenico Galli
!!
!!
!!
!!
!!
Quando il cilindro rotola su di una superficie, si crea
sulla superficie una avvallamento che procede insieme al
cilindro.
!!
Dove si forma l’avvallamento sono presenti forze che si
oppongono alla deformazione.
Fisica Generale A. 5. Statica. 31
Domenico Galli
Il rallentamento del moto di rotolamento (come
vedremo in dinamica) è dovuto a una coppia di forze.
Tale coppia è detta coppia di attrito volvente. Si
tratta di forze assolutamente diverse da quelle di
attrito radente statico.
!
Rt(s)
!
F
Attrito volvente (III)
L’attrito volvente ha origine in una asimmetria delle
forze elastiche vincolari.
Dove l’avvallamento scompare sono presenti forze di
ripristino.
Se le forze che si oppongono alla
deformazione non sono esattamente uguali
alle forze di ripristino, si ha un’asimmetria
che genera l’attrito volvente.
La forza di attrito radente statico non ostacola il
rotolamento del cilindro.
Fisica Generale A. 5. Statica. 30
Domenico Galli
Attrito volvente (II)
!!
Un cilindro che rotola senza strisciare su di un piano è
soggetto alla forza di attrito radente statico che
impedisce lo strisciamento.
!!
!
F
L’attrito volvente risulta molto inferiore all’attrito
radente (dalle 100 alle 1000 volte).
Per questo motivo, dove si debba minimizzare l’attrito
nella rotazione di un asse, si preferiscono i cuscinetti
a rotolamento (come il cuscinetto a sfere mostrato
in figura) ai cuscinetti a strisciamento (p.es.:
bronzine).
Tra le due superfici cilindriche
in figura sono poste 9 sfere
ingabbiate che rotolano quando
una superficie cilindrica si
muove rispetto all’altra.
Fisica Generale A. 5. Statica. 32
Domenico Galli
Forze di attrito (note)
!!
!!
!!
Un corpo che striscia su di una superficie è soggetto
alla forza di attrito radente dinamico.
Un corpo che rotola senza strisciare su di una
superficie è soggetto alla forza di attrito radente
statico e alla forza di attrito volvente.
In assenza di attrito radente l’uomo e gli animali
non riuscirebbero a camminare e gli autoveicoli non
riuscirebbero a muoversi.
!
Rt(s)
Fisica Generale A. 5. Statica. 33
Domenico Galli
!
Rt(s)