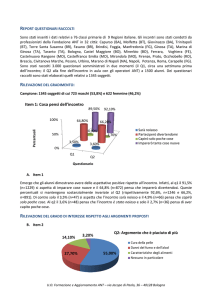
Approfondimento 4.6
La valutazione statistica della discriminatività di un item
1. Item di test di prestazione massima
Per valutare la discriminatività di un item di un test di prestazione massima occorre confrontare fra
loro le proporzioni di risposta corretta di ogni item fra i gruppi di soggetti definiti dal quantile massimo e dal quantile minimo della distribuzione dei punteggi totali al test. Nel manuale viene suggerito che la divisione può essere fatta in due parti tramite la mediana, oppure in tre, quattro o cinque
parti, e che all’aumentare delle parti in cui è suddivisa la distribuzione dei punteggi totali il test diventa più sensibile. In questo esempio la distribuzione verrà divisa in quartili, ma la procedura è identica per qualunque altro numero di parti si voglia dividere la distribuzione.
Nel seguente esempio utilizziamo il file “RASCH1.sav”, scaricabile dal sito online del manuale. Il file è composto da 13 colonne, corrispondenti alle 13 domande del file
“Test_pedagogia.doc”, e da 328 righe, corrispondenti ai soggetti. I valori 0 e 1 indicano, rispettivamente, risposta errata e corretta. I dati sono già correttamente codificati, per cui, utilizzando la funzione Compute descritta nell’Approfondimento 4.4, Sezione 4, calcoliamo il punteggio totale. Andiamo al menu Transform→Compute e nei campi appositi della finestra che si apre indichiamo il
nome della variabile che conterrà il punteggio totale (tot) e la somma degli item (Figura 4.6.1).
Figura 4.6.1 Calcolo del punteggio totale per i dati del file RASCH1.sav
Una volta clickato OK comparirà nel file di dati una nuova colonna chiamata tot.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
2
A questo punto abbiamo bisogno di suddividere in quartili questa distribuzione. Per farlo,
andiamo al menu Transform→Rank cases. Nella finestra che si aprirà inseriamo la variabile tot nel
campo Variable(s) e clickiamo su Rank Types. Nella nuova finestra (Figura 4.6.2) deselezioniamo
l’opzione di default Rank e selezioniamo invece Ntiles. Accanto all’opzione c’è un numero, che è
appunto il numero di parti in cui vogliamo dividere la distribuzione. Come è ovvio, se desiderate
dividere la distribuzione in terzili o quintili basta cambiare questo numero.
Figura 4.6.2 Finestre Rank Cases e Rank Cases: Types
Clickiamo su Continue e poi su OK. Si aprirà una finestra di output che riporterà la dicitura
Variables Created By RANK
tot into Ntot(NTILES of tot)
e nel file di dati comparirà un’altra colonna chiamata Ntot. Quello che vogliamo fare adesso è confrontare se le proporzioni di risposte corrette nel quarto quartile sono statisticamente maggiori di
quelle del primo quartile. Purtroppo non possiamo farlo direttamente con SPSS, ma possiamo utilizzare SPSS per calcolare i dati da incollare nel file DISCRIM.xls scaricabile dal sito del manuale.
Quello che facciamo, quindi, è utilizzare la procedura di SPSS che permette di realizzare un test per
campioni indipendenti, ma dell’outpur risultante consideremo solo le statistiche descrittive, ignorando il test di ipotesi.
Andiamo a Analyze→Compare Means→Independent Samples T Test e inseriamo tutti gli item nel campo Test Variable(s) e la variabile Ntot nel campo Grouping Variable. A questo punto
clickiamo su Define Groups e indichiamo che i due gruppi da confrontare sono l’1 e il 4 (Figura
4.6.3).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
3
Figura 4.6.3 Indicazione dei gruppi da confrontare in SPSS
Clickiamo su Continue e quindi su OK. A questo punto nella finestra di output comparirà la tabella
Group Statistics (Figura 4.6.4) e la tabella Independent Samples Test.
Group Statistics
d01
d02
d03
d04
d05
d06
d07
d08
d09
d10
d11
d12
d13
NTILES of tot
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
N
79
97
79
97
79
97
79
97
79
97
79
97
79
97
79
97
79
97
79
97
79
97
79
97
79
97
Mean
.15
.75
.18
.70
.49
.89
.44
.85
.44
.95
.15
.70
.76
.94
.19
.86
.03
.34
.53
.98
.06
.30
.38
.91
.20
.87
Std. Deviation
.361
.434
.384
.460
.503
.319
.500
.363
.500
.222
.361
.460
.430
.242
.395
.353
.158
.476
.502
.143
.245
.460
.488
.292
.404
.342
Std. Error
Mean
.041
.044
.043
.047
.057
.032
.056
.037
.056
.023
.041
.047
.048
.025
.044
.036
.018
.048
.057
.015
.028
.047
.055
.030
.046
.035
Figura 4.6.4 Tabella dei risultati Group Statistics per gli item del file RASCH1.sav
Se le risposte sono state codificate come 0=sbagliata e 1=corretta, la media dei valori corrisponderà
alla proporzione di risposte corrette. A questo punto apriamo il file DISCRIM.xls e selezioniamo il
foglio PROPORZIONI. Torniamo all’output di SPSS, selezioniamo la prima tabella, copiamo
(CTRL+C) 1, andiamo al file DISCRIM, foglio PROPORZIONI, selezioniamo la casella A1 e incol-
1
Oppure clickare col tasto destro del mouse e scegliere Copia.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
4
liamo (CTRL+V)2. Nelle celle di gialle compariranno i dati che abbiamo incollato, mentre le celle
bianche calcoleranno automaticamente gli indici citati nel testo (Figura 4.6.5).
Figura 4.6.5 File DISCRIM.xls, foglio PROPORZIONI
Per ogni item viene eseguito il test di significatività, da cui un valore di z e di p (colonne L e M),
viene calcolata la discriminatività D (colonna O), la dimensione dell’effetto h (colonna R) e l’indice
di difficoltà di Ebel (colonna U). I commenti accanto a questi tre indici sono quelli riportati, rispettivamente, nelle Tabelle 4.9, 4.10 e 4.7 del manuale.
Si noti come le ampie numerosità campionarie influenzino la significatività del test z (in cui
la logica è: se p < ,05 la discriminatività adeguata, altrimenti no) mentre gli altri indici forniscano
un quadro più attendibile della discriminatività di ogni item. Abbiamo quindi che l’item d07 non
sembra offrire un’adeguata discriminatività, mentre gli buona parte degli altri item presentano
un’ottima discriminatività, un indice di dimensione dell’effetto alto e un indice di difficoltà ottimale.
I dettagli statistici della verifica delle ipotesi per il confronto di due proporzioni indipendenti
possono essere trovati in Chiorri (2010), Capitolo 5, Sezione 5.1.1.
2. Item di test di prestazione tipica
Nel caso degli item di prestazione tipica, il procedimento è identico a quello appena illustrato per i
test di prestazione massima. Per riprodurre i risultati dell’esempio che segue occorre utilizzare il file
di dati TIPICA1.sav. In questo file sono contenute le risposte di 386 soggetti a 7 item di tipo Likert
a 5 punti.
Con lo stesso procedimento visto nella sezione 1 di questo approfondimento calcoliamo il
punteggio massimo tot e il rango quartile (Ntile) per ogni soggetto. Poi eseguiamo il medesimo procedimento per realizzare il test t per campioni indipendenti, e otteniamo la tabella Group Statistics
(Figura 4.6.6)
2
Oppure clickare col tasto destro del mouse e scegliere Incolla.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
5
Group Statistics
i01
i02
i03
i04
i05
i06
i07
NTILES of tot
1
4
1
4
1
4
1
4
1
4
1
4
1
4
N
93
113
93
113
93
113
93
113
93
113
93
113
93
113
Mean
1.97
4.76
2.16
4.83
1.87
4.88
2.14
5.00
1.68
3.54
2.59
4.93
2.01
4.98
Std. Deviation
1.047
.449
1.076
.441
.923
.357
1.315
.000
.810
.708
1.236
.258
1.433
.132
Std. Error
Mean
.109
.042
.112
.042
.096
.034
.136
.000
.084
.067
.128
.024
.149
.012
Figura 4.6.6 Tabella dei risultati Group Statistics per gli item del file TIPICA1.sav
Analogamente al caso precedente, copiamo e incolliamo la tabella nella cella A1 del file DISCRIM.xls, questa volta nel foglio MEDIE. I risultati sono riportati in Figura 4.6.7
Figura 4.6.7 File DISCRIM.xls, foglio MEDIE
In questo caso viene effettivamente realizzato un test t per campioni indipendenti, ma con la formula corretta per le varianze non omogenee (da cui il numero di gradi di libertà con la virgola). Questo
accorgimento si rende necessario in quanto non sempre le varianze dei due gruppi sono omogenee
fra di loro. Ad ogni modo, quello che ci interessa valutare è la dimensione dell’effetto d, il cui
commento segue le indicazioni: d < 0,20 trascurabile, 0,20 < d < 0,50 piccolo, 0,50 < d < 0,80 moderato e d > 0,80 grande.
In base ai risultati presentati in Figura 4.6.7 risulta evidente come tutti gli item presentino un
alto livello di discriminatività.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
6
I dettagli statistici della verifica delle ipotesi per il confronto di due medie di campioni indipendenti possono essere trovati in Chiorri (2010), Capitolo 5, Sezione 5.1.3.
3. Discriminatività fra gruppi precostituiti
Quando il test è orientato al criterio, l’item analysis si focalizza soprattutto sull’individuare quegli
item che meglio consentono la discriminazione fra i due gruppi. In questi casi la discriminatività di
ogni item viene valutata confrontando le proporzioni o le medie dei due gruppi di soggetti, senza ricorrere alla suddivisione dei soggetti in quartili in base al punteggio totale. In questi casi le analisi
di discriminatività vengono eseguite esattamente come nei casi che abbiamo visto nelle sezioni 1 e
2, solo che la variabile di raggruppamento da inserire nel campo Grouping Variable (vedi Figura
4.6.3) non sarà il rango quartile, ma il gruppo a cui i soggetti appartengono, che, a seconda dei casi,
sarà una variabile che contiene informazioni sul genere, sul fatto di appartenere al campione di popolazione generale o a quello della popolazione clinica, sul fatto di appartenere al gruppo sperimentale o a quello di controllo, e così via. In questi casi, per massimizzare la capacità discriminativa del
punteggio al test è consigliabile mantenere nel pool di item quegli item che abbiano un livello di discriminatività D almeno “Buono” e un indice di dimensione dell’effetto almeno “Moderato”.
Quando si lavora su gruppi precostituiti non è raro che i gruppi che si vogliono discriminare
fra loro siano più di due. In questi casi occorre utilizzare tecniche di analisi che tengano conto della
presenza di più di due gruppi e ci consentano di valutare se, in generale, almeno due gruppi differiscono significativamente fra di loro, e, se sì, quali. Il ricercatore, infatti, potrebbe essere interessato
a selezionare item che distinguano tutti i gruppi fra di loro, oppure solo alcuni specifici. Se la verifica dell’ipotesi nulla che tutti i gruppi facciano riferimento a popolazioni con proporzioni o medie
uguali viene realizzata mediante il cosiddetto test omnibus, la verifica dell’ipotesi nulla che alcune
coppie di gruppi non differiscano fra loro può essere eseguita mediante i test post-hoc.
3.2 Discriminatività fra gruppi precostituiti: caso delle proporzioni
Nel file RASCH2.sav sono riportati i dati di sei prove attentive (0 = non superata, 1 = superata) che possono essere utilizzati per discriminare fra tre gruppi di soggetti: lesione cerebrale specifica (codificato come 1 nella variabile gruppo), lesione cerebrale generica (codificato come 2 nella
variabile gruppo) e popolazione generale (codificato come 3 nella variabile gruppo). In questo caso
vogliamo verificare se le proporzioni di soggetti che superano ogni singola prova attentiva sono le
stesse per tutti e tre i gruppi. Per riuscirvi dobbiamo applicare il test per il confronto di k proporzioni indipendenti. Vediamo come procedere per l’item01.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
7
Innanzitutto abbiamo bisogno di realizzare una tavola di contingenza con la variabile gruppo
sulle righe e il risultato della prova sulle colonne. Per farlo con SPSS seguiamo Analyze→Descriptive Statistics→Crosstabs. Inseriamo la variabile gruppo nel campo Row(s) e la variabile d01 nel campo Column(s) (Figura 4.6.8).
Figura 4.6.8 Eseguire un’analisi per il confronto di k proporzioni indipendenti in SPSS
A questo punto clickiamo su Statistics e nella nuova finestra spuntiamo in alto a sinistra Chisquare, e poi Continue. Poi clickiamo su Cells, lasciamo selezionato Observed e spuntiamo nel Row
nel riquadro Percentages, quindi Continue (Figura 4.6.9).
Figura 4.6.9 Opzioni per il confronto di k proporzioni indipendenti in SPSS
A questo punto clickiamo OK. Nei risultati le tabelle che ci interessano sono quelle chiamate gruppo * d01 Crosstabulation e Chi-Square Tests (Figura 4.6.10).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
8
gruppo * d01 Crosstabulation
d01
gruppo
Lesione specifica
Lesione generica
Popolazione generale
Total
Count
% within gruppo
Count
% within gruppo
Count
% within gruppo
Count
% within gruppo
Non supera
l'item
43
67.2%
35
48.6%
18
28.1%
96
48.0%
Supera l'item
21
32.8%
37
51.4%
46
71.9%
104
52.0%
Total
64
100.0%
72
100.0%
64
100.0%
200
100.0%
Chi-Square Tests
Pearson Chi-Square
Likelihood Ratio
Linear-by-Linear
Association
N of Valid Cases
Value
19.579a
20.129
2
2
Asymp. Sig.
(2-sided)
.000
.000
1
.000
df
19.465
200
a. 0 cells (.0%) have expected count less than 5. The
minimum expected count is 30.72.
Figura 4.6.10 Tabelle di output di SPSS per il confronto di k proporzioni indipendenti
Innanzitutto dobbiamo verificare, per un livello di significatività del 5% (ossia, α = ,05) se possiamo rifiutare l’ipotesi nulla che i tre gruppi facciano riferimento a popolazioni con la stessa proporzione di individui che superano la prova. Nella tabella Chi-Square Tests valutiamo la significatività
del test Pearson Chi-Square [colonna Asymp. Sig. (2-sided)] che è inferiore a ,05. Questo significa
che possiamo rifiutare l’ipotesi nulla e accettare quella alternativa che almeno due proporzioni siano
diverse fra loro. A questo punto, però, calcoliamo la dimensione dell’effetto w, perché la significatività del test omnibus potrebbe essere dovuta semplicemente all’alto numero di soggetti. Per calcolarla applichiamo la formula:
w=
X2
19,579
=
=,31
n
200
Questo valore viene interpretato nel seguente modo: w < ,10 trascurabile, ,10 < w < ,30 piccolo, ,30
< w < ,50 moderato e w > ,50 grande. Poiché il w ottenuto è uguale a ,31, possiamo concludere che
la dimensione dell’effetto del test omnibus è moderata, e quindi adeguata.
Nondimeno, ora vogliamo sapere quali gruppi differiscono fra loro quanto a proporzione di
soggetti che superano la prova. Esiste una tecnica statistica (descritta in Chiorri, 2010, Approfondimento 6.1), ma a noi interesserà soprattutto la dimensione dell’effetto, per cui calcoliamo direttamente quella. La dimensione dell’effetto h per il confronto fra due proporzioni indipendenti si calcola come:
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
9
h = 2arcsen P1 − 2arcsen P2
In base ai dati della tavola di contingenza in Figura 4.6.10, colonna Supera l’item, calcoliamo le tre
dimensioni dell’effetto:
Confronto popolazione generale vs lesione specifica: h = 2arcsen ,719 − 2arcsen ,328 = 0,80
Confronto popolazione generale vs lesione generica: h = 2arcsen ,719 − 2arcsen ,514 = 0,43
Confronto lesione generica vs lesione specifica: h = 2arcsen ,514 − 2arcsen ,328 = 0,38
La dimensione dell’effetto h viene interpretata: h < 0,20 trascurabile, 0,20 < h < 0,50 piccolo, 0,50
< h < 0,80 moderato e h > 0,80 grande. In base ai risultati possiamo concludere che la discriminatività dell’item è grande per il confronto popolazione generale vs lesione specifica, ma piccola per il
confronto fra popolazione generale e lesione generica e fra lesione generica e lesione specifica. La
domanda che occorre porsi a questo punto è: tali livelli sono sufficienti? Se infatti l’item discrimina
bene fra popolazione generale e lesione specifica, la sua capacità di discriminare fra le altre coppie
possibili di gruppi non appare molto elevata, per cui, dopo aver valutato anche i risultati ottenuti
con gli altri item, occorrerà considerare con attenzione se mantenere l’item nel test oppure no.
3.3 Discriminatività fra gruppi precostituiti: caso delle medie
Il file TIPICA3.sav è di fatto identico al file RASCH2.sav che abbiamo appena utilizzato, con la
differenza che gli item contengono risposte su scala Likert da 1=per niente d’accordo a
6=completamente d’accordo di tre gruppi di soggetti: pazienti con disturbo di personalità (DP) narcisistico (codificato come 1 nella variabile gruppo), pazienti con DP generico (codificato come 2
nella variabile gruppo) e popolazione generale (codificato come 3 nella variabile gruppo). Lo scopo
dell’analisi è verificare se i pazienti con DP narcisistico ottengono punteggi più alti degli altri due
gruppi. La logica è esattamente la stessa del test sulle k proporzioni indipendenti, solo che stavolta
l’ipotesi nulla è che le medie delle tre popolazioni a cui fanno riferimento i tre gruppi siano uguali.
Per verificare l’ipotesi con SPSS utilizziamo l’analisi della varianza (ANOVA) ad una via.
Seguiamo Analyze→Compare Means→One-Way ANOVA, e inseriamo la variabile d01 nel campo
Dependent List e la variabile gruppo nel campo Factor (Figura 4.6.11).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
10
Figura 4.6.11 Procedura di SPSS per il realizzare un’ANOVA
Clickiamo su Post-Hoc, spuntiamo Games-Howell nel riquadro Equal Variances Not Assumed e poi
Continue. Questo ci consentirà di eseguire i test post-hoc per verificare, se il test omnibus è significativo, quali medie differiscono statisticamente fra di loro. Poi clickiamo su Options , spuntiamo
Descriptive e poi clickiamo Continue (Figura 4.6.12) Questo ci consentirà di ottenere nell’output le
statistiche descrittive dei tre gruppi
Figura 4.6.12 Opzioni di SPSS per l’ANOVA
Clickiamo OK e otteniamo l’output (Figura 4.6.13).
Descriptives
d01
N
DP narcisistico
DP generico
Popolazione generale
Total
59
69
72
200
Mean
4.49
3.58
2.31
3.39
Std. Deviation
1.023
1.168
1.194
1.442
Std. Error
.133
.141
.141
.102
95% Confidence Interval for
Mean
Lower Bound Upper Bound
4.22
4.76
3.30
3.86
2.02
2.59
3.19
3.59
Minimum
3
2
1
1
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Maximum
6
5
4
6
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
11
ANOVA
d01
Between Groups
Within Groups
Total
Sum of
Squares
158.745
254.835
413.580
df
2
197
199
Mean Square
79.372
1.294
F
61.359
Sig.
.000
Multiple Comparisons
Dependent Variable: d01
Games-Howell
(I) gruppo
DP narcisistico
DP generico
Popolazione generale
(J) gruppo
DP generico
Popolazione generale
DP narcisistico
Popolazione generale
DP narcisistico
DP generico
Mean
Difference
(I-J)
.912*
2.186*
-.912*
1.274*
-2.186*
-1.274*
Std. Error
.194
.194
.194
.199
.194
.199
Sig.
.000
.000
.000
.000
.000
.000
95% Confidence Interval
Lower Bound Upper Bound
.45
1.37
1.73
2.65
-1.37
-.45
.80
1.75
-2.65
-1.73
-1.75
-.80
*. The mean difference is significant at the .05 level.
Figura 4.6.13 Output di SPSS per l’ANOVA
Dalla prima tabella (Descriptives) osserviamo che le tre medie sono perlomeno nell’ordine atteso,
ossia con i pazienti di DP narcisistico che mostrano i punteggi maggiori, seguiti nell’ordine dai DP
generici e della popolazione generale. La seconda tabella (ANOVA) mostra che il test omnibus è significativo, per cui possiamo rifiutare l’ipotesi nulla che le medie delle popolazioni a cui fanno riferimento i tre gruppi siano uguali. La dimensione dell’effetto può essere calcolata come ω2 con la
formula:
ω2 =
SS between − (k − 1) MS within
SS totale − MS within
dove SS sta per Sum of Squares, ossia devianza, MS sta per Mean of Squares, ossia varianza, e k è il
numero di gruppi. I valori che ci servono sono proprio nella colonna omonima della tabella ANOVA:
ω2 =
158,745 − (3 − 1) × 1,294
=,38
413,580 − 1,294
La dimensione dell’effetto ω2 viene interpretata: ω2 < ,01 trascurabile, ,01 < ω2h < ,06 piccolo, ,06
< ω2 < ,15 moderato e ω2 > ,15 grande, per cui ci troviamo di fronte ad un effetto grande.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.6 – La valutazione statistica della discriminatività di un item
12
I test post-hoc nella tabella Multiple Comparisons confermano la capacità del test di discriminare fra i gruppi, dato che tutti i confronti sono statisticamente significativi (vedi la colonna Sig.:
tutti i valori sono inferiori a ,05). Si noti che in questo caso non c’è bisogno di considerare la correzione del livello di significatività per i confronti multipli in quanto è già incorporata nel test eseguito dal software.
Per calcolare la dimensione dell’effetto dei test post-hoc abbiamo bisogno di calcolare, a
partire dai valori della tabella Multiple Comparisons, il valore di q, che è dato dal rapporto fra i valori nella colonna Mean Difference (I−J) e quelli nella colonna Std. Error. Nel caso del confronto
DP narcisistico vs Dp generico avremo che q = ,912 / ,194 = 4,70, e allo stesso modo calcoliamo i q
per DP narcisistico vs Popolazione generale (2,186 / ,194 = 11,27) e DP generico vs Popolazione
generale (1,274 / ,194 = 6,40). A questo punto la dimensiona dell’effetto r per ogni confronto è data
dalla formula:
r=
(q / 2 ) 2
(q / 2 ) 2 + df within
dove dfwithin sono i gradi di libertà della varianza within. Dalla tabella ANOVA ricaviamo che questo
valore è 197. La dimensione dell’effetto r viene interpretata come: r < ,10 trascurabile, ,10 < r < ,30
piccolo, ,30 < r < ,50 moderato e r > ,50 grande, per cui avremo che:
Confronto DP narcisistico vs DP generico: r =
(4,70 / 2 ) 2
(4,70 / 2 ) 2 + 197
Confronto DP narcisistico vs popolazione generale: r =
Confronto DP generico vs popolazione generale: r =
=,23
(11,27 / 2 ) 2
(11,27 / 2 ) 2 + 197
(6,40 / 2 ) 2
(6,40 / 2 ) 2 + 197
=,56
=,32
Dalle dimensioni dell’effetto osserviamo che il test discrimina molto bene fra DP narcisistico e popolazione generale, ad un livello basso fra DP narcisistico e generico e moderato fra DP generico e
popolazione generale. Anche in questo caso, naturalmente, sta al ricercatore decidere se questi livelli sono sufficienti per i suoi scopi oppure no.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia