espressione teorica delle forze di Van der Waals

estratto da :
L’EQUILIBRIO UNIVERSALE
dalla meccanica celeste alla fisica nucleare
– Espressione teorica delle forze di Van der Waals e dei raggi atomici
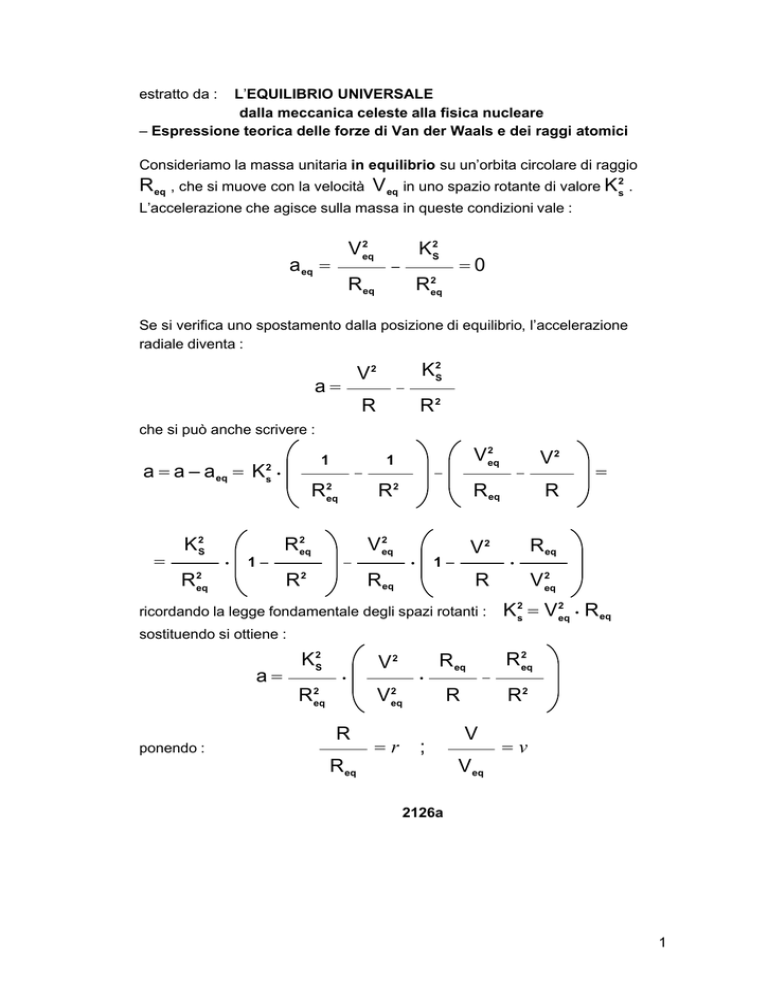
Consideriamo la massa unitaria in equilibrio su un’orbita circolare di raggio
R eq , che si muove con la velocità V eq in uno spazio rotante di valore K 2s .
L’accelerazione che agisce sulla massa in queste condizioni vale :
V 2eq
a eq 
K 2S
–
R eq
R
0
2
eq
Se si verifica uno spostamento dalla posizione di equilibrio, l’accelerazione
radiale diventa :
V2
a
K 2S

R2
R
che si può anche scrivere :
a  a – a eq  K

K 2S
R

2
s
1

1–
2
eq
R
R 2eq
R

2
eq
1
R

2
V 2eq

2
V2

R eq
V 2eq

V2
1–
R eq
R

R eq
V 2eq
R
ricordando la legge fondamentale degli spazi rotanti :

K 2s  V 2eq  R eq
sostituendo si ottiene :
a
K 2S
R
ponendo :

2
eq
V2
V
R

R eq
2
eq
r

R2
R
;
R eq
R 2eq
V
v
V eq
2126a
1
K 2S
a
si può scrivere :
R
2

–
r
2
eq
1
.
r2
Se lo spostamento dalla posizione di equilibrio avviene senza dover
applicare un momento esterno, il momento angolare della massa in
moto rotorivoluente si mantiene costante su tutta l’orbita e quindi è
verificata la relazione :
V  R  V eq  R eq
da cui si ricava :
V
R eq

V eq
1
v
ossia :
r
R
in definitiva, l’accelerazione che lo spazio rotante esercita sulla massa che si
muove sull’orbita risulta espressa dalla relazione :
a
K 2S
R

2
eq
r 3  r 2
oppure :
a
K 2S
R
3

R eq – R
che, per piccoli spostamenti, si può anche scrivere :
a–
K 2S
 R
–
R 3eq
K 2S

R 2eq
Per esempio, per produrre una riduzione del raggio
R
R eq
R
 10 6 nell’atomo
R eq
di idrogeno, è necessario applicare all’elettrone una forza uguale a :
F  a  m e  10
6

K 2p
 m e  8. 23873  10 14 Nw
R 211e
La pressione che si deve esercitare sulla sfera planetaria dell’elettrone dovrà
essere :
2126b
2
P
F
  R 2P0e
 3. 1574  10 13
Nw
m
2
 315. 74  10 6 atm
Riportando su diagramma cartesiano, si ottiene l’andamento riportato nella
figura seguente, che mette in evidenza " una grande stabilità dell’ orbita "
per piccoli spostamenti della massa satellite.
Dal diagramma risulta infatti che una qualsiasi variazione del raggio genera
sempre un’accelerazione tale da riportarlo al valore di equilibrio R eq .
Se nell’espressione dell’accelerazionesi sostituisce a R eq il valore del raggio
esterno di un atomo, il diagramma coincide esattamente con quello che
si rileva sperimentalmente per le forze di Van der Waals di cui non si
conosce l’espressione teorica.
Il calcolo dimostra però che esse possono essere descritte come particolare
applicazione della teoria degli spazi rotanti, che ha validità assolutamente
generale ed è applicabile in tutto l’intervallo
0 R ; m


Derivando e annullando l’espressione di a , si ricava il valore R
.

3
 Rn
2
2126c
3
in corrispondenza del quale l’accelerazione centripeta risulta massima.
Sostituendo :
R1
Rn 
oppure
Rp 
R1  p2
n2
si ricava l’accelerazione
an
in prossimità delle orbite stabili in tutto il
raggio d’azione dello spazio rotante .
Se la massa si trova tra due livelli stabili vicini p e
p1
, ossia se si ha
RP
 R  R P1 , l’accelerazione che sollecita la massa verso la condizione
di equilibrio sarà data dalla somma delle accelerazioni :
a  a P  a P1 
K 2S  R 1

p
2

2
p1
–2 
R3
e cambia segno quando si verifica
R
R1
p2  p  1
2
–2
R
0
con la
R1
massa equidistante dai due punti di equilibrio.
Moltiplicando l’accelerazione per la massa planetaria considerata, si ottiene
l’espressione della forza, con l’andamento indicato in figura.
2126d
4
K 2S
F
Si ha dunque :

m
 r 3  r 2 
R 2P
Questa relazione esprime dunque la forza che spinge la massa m verso una
condizione di equilibrio stabile e si annulla in corrispondenza dei punti in cui
R
essa viene raggiunta, ossia
 p 2  1 ; 4 ; 9 ; 16 ; ecc.....
R1
La forza si annulla anche nei punti di flesso intermedi. Si tratta però di punti di
equilibrio instabile, per cui risultano tutte zone vuote.
Dato che l’espressione indica anche la forza che richiama la massa m nella
condizione di equilibrio quando essa ne viene allontanata, possiamo anche
dire che indica la forza di un legame.
Può quindi essere conveniente esprimere la forza F in funzione dell’energia
che lega la massa allo spazio rotante centrale, ricordando che essa è uguale
a metà dell’energia potenziale, ossia :
E Pm 
1
 Fs  RP

2
1

2
K 2S  m
R
 RP
2
P
Sostituendo, abbiamo :
F
K 2S

R
m
 r
3
2
r 

2
P
2  E Pm
 r 2  r 1 
R
Avendo ricavato la relazione senza alcuna ipotesi restrittiva, essa sarà
applicabile a tutti gli spazi rotanti, indipendentemente dalle dimensioni.
" Lo stesso diagramma " rappresenta quindi sia le forze
che si manifestano nell’atomo oppure nel nucleo atomico
che quelle imposte dallo spazio rotante solare sui pianeti
che si muovono in equilibrio sulle sue orbite stabili.
Se consideriamo lo spazio rotante atomico agente su un elettrone già legato
2126e
5
sul livello di confine di un altro atomo, è chiaro che, essendo l’elettrone legato
con il nucleo, l’azione che si esercita su di esso si trasferisce integralmente a
tutto l’atomo.
In questo caso l’espressione teorica che abbiamo ricavato descrive la forza
d’interazione tra i due atomi al variare della loro distanza , nota come forza
di Van der Waals, di cui le teorie correnti non forniscono alcuna espressione
teorica, ma conoscono il suo comportamento attraverso i rilievi sperimentali,
che portano praticamente a risultati coincidenti con quelli che si ottengono
teoricamente.
Sostituendo, nell’espressione della forza le relazioni note :
1
3
m  m e ; K 2s  Z  K 2p ; R p  R 11e  Z
2
 ps
si ottiene :
F
K 2S

R
m
 r
3
2
r 
Z  K 2p

2
P
me
 r 3  r 2 
2
R 211e  Z
posto :

F 11e 
K 2p

me

3
4
 ps
82. 38729472  10  9 N w
R 211e
1
F  F 11e 
si ottiene :
3
Z
 r 3  r 2 
p 4s
Se consideriamo, per esempio, un atomo di zinco, con Z
 30
e ps
4
si ottiene :
F Zne  9. 9998625  10  10 N w  r 3  r 2 
Per
r 
R
1
si ha
F Zne  0
e quindi l’azione è repulsiva
R eq
Per
Per
r  1 e r   si hanno le condizioni di equilibrio con F Zne  0
r  1 risulta F Zne  0 e si ha quindi una forza attrattiva che raggiunge
2126f
6
il valore massimo in corrispondenza del valore r
3

.
2
Nelle teorie correnti non sono disponibili equazioni ricavate teoricamente per
descrivere le forze interatomiche, dunque ci si deve affidare a espressioni
che vengono ricavate empiricamente.
La più nota di queste funzioni è il potenziale di Lennard – Jones, che si può
scrivere nella forma :
V

4
r
12
6

–
r
r
in cui  rappresenta il valore della buca di potenziale, che viene associata
all’atomo considerato e  le sue dimensioni.
Da questa relazione si ricava l’espressione empirica della forza :
F
r
4



r
6

–
r
r
6

che, se poniamo :
12
RP

r

1
r
R
risulta formalmente coincidente con l’espressione teorica da noi ottenuta :
F
R

K 2S

m
 r 3  r 2 
R 2P

2  E Pm
 r 2  r 1 
R
Con riferimento allo spazio rotante atomico, l’energia E Pm diventa :
E Pm 
1
2

K 2S  m
R 2P
 RP

1
Z  K 2p

2

me
1
R 11e  Z
3
p
2
2126g
7
semplificando e sostituendo i valori numerici, si ottiene :
2
3
Z
E Pm  13. 60569806 eV 
p2
L’espressione della forza diventa quindi :
2
F

R
27. 21139612 eV

Z
3
 r 2  r 1 
p2
R
oppure, per piccoli spostamenti dalla posizione di equilibrio, si ha :
1
R  R p  R 11e  Z
3
p
F
R
2
e quindi, sostituendo :

F 11e
p
 r 2  r 1 
4
La relazione è stata ricavara considerando l’interazione di una sola massa
su una sola orbita e quindi si può applicare identicamente solo in questi
casi. Per esempio, la forza che lo spazio rotante solare esercita sulla Terra,
quando essa si sposta dalla sua orbita di equilibrio risulta :
F Teq 
F 11S
p 4T
e quindi :
FT
R

K 2s  m T
 3. 54404  10 22 N w
R 2T
 3. 54404  10 22 N w 
R 2T
R2

RT
R
con l’andamento tipico delle forze di Van der Waals.
Ne caso in cui si considera l’interazione tra due spazi rotanti organizzati con
molte masse distribuite su molti livelli stabili, come per esempio due galassie
oppure due atomi o due nuclei, l’interazione si realizza come è schematizzato
nella figura seguente.
2126h
8
Quando i due masse periferiche arrivano nella zona centrale C, interagiscono
attraverso la loro sfera planetaria di raggio R P0 con una accelerazione :
a
V 2mm
d mm

K 2m
d 2mm

V 2mm
d mm

V 2eqm
d mm

1
d mm
2
2
V mm  V eqm
dove V eqm rappresenta la velocità di equilibrio imposta dallo spazio rotante
generato dalla massa m sull’orbita di raggio uguale alla distanza
d mm tra le
due masse interagenti e V mm la loro velocità delativa, che coincide con il
doppio della velocità di equilibrio che le masse avevano sull’orbita iniziale
dello spazio rotante centrale.
Dato che La massa che genera lo spazio rotante centrale è sempre di gran
lunga maggiore di quella presente sulle orbite, risulta V mm  V eqm .
L’accelerazione risulta dunque repulsiva e le due masse si scambiano la loro
posizione sulle orbite, come è indicato in figura.
In definitiva le due masse si trovano a percorrere un’orbita deformata attorno
ai due nuclei, come se si trattasse di uno solo.
Naturalmente, il processo si ripete per tutte le masse presenti sul livello di
confine.
Quando queste sono esaurite, l’interazione passa sul penultimo livello, poi sul
terzultimo e così via fino al livello fondamentale, associato a
p  1.
Se indichiamo con m A ed m B le due masse solari, alla fine del processo si
2126i
9
avranno tutte le masse satelliti in orbita attorno ai due nuclei, che formano un
sistema doppio alla distanza minima uguale alla somma dei raggi delle loro
orbite fondamentali : d AB  R 1A  R 1B .
Generalmente, quando il calcolo viene riferito all’atomo, si fa riferimento a due
atomi dello stesso elemento e quindi si ottiene teoricamente :
1
3
d AB  2  R 1  2  R 11e  Z
Il raggio della sfera planetaria associabile ad un singolo nucleo viene assunto
come raggio di Van der Waals e risulta, in prima approssimazione :
1
3
R VdW  R 1  R 11e  Z
La relazione è molto approssimata, in quanto non prende in alcun modo in
considerazione la reale distribuzione degli elettroni sulle diverse orbite.
Nei rilievi sperimentali l’interazione tra gli atomi si realizza con una parziale
sovrapposizione delle due sfere fondamentali di circa 15  25% in rapporto
all’elemento considerato, dunque mediamente del 20% .
Generalmente il valore del raggio atomico covalente ricavato per questa via
risulta dunque :
1
3
R ac  0. 8  R 11e  Z
I valori limiti, per l’intervallo che comprende gli elementi
Z  1  92
risultano:
R ac 1   42  10 12 m
R ac 92   191  10 12 m
;
Il valore massimo del raggio entro il quale è apprezzabile l’azione delle forze
di Van der Waals, definito come raggio d’azione, vale, approssimativamente
1
R aVdW 
3
2
 RP
S

3
 R 11e 
Z
2
Per esempio, per l’atomo di stagno, con Z  50 e p s
R aVdW 50 
3
1
 5. 29  10 11 m  50 3  5
2
3
2
 ps
 5 , risulta :
 73. 11  10 10 m
2
Normalmente siconsidera la distanza fra i centri di due atomi interagenti, per
cui si assume un valore doppio.
2126l
10