Controllo e scheduling delle
operazioni
Paolo Detti
Dipartimento di Ingegneria dell’Informazione
Università di Siena
Organizzazione della produzione
PRODOTTO che cosa
chi
ORGANIZZAZIONE
come
PROCESSO
COORDINAMENTO
FLUSSO DI PRODUZIONE
PIANIFICAZIONE
SCHEDULING
quando
Pianificazione della produzione:
schedulazione di dettaglio
Sono dati:
• Un insieme di lavori (job): ognuno costituito da
una o più operazioni
• Un insieme di risorse (macchine) che devono
essere utilizzate per eseguire i lavori
Scheduling delle operazioni
Scelta dei tempi di inizio e fine di ogni
operazione su ogni macchina
Scheduling delle operazioni
Consideriamo:
3 lavori e 3 macchine
Job
J1
Sequenza delle operazioni
operazione=(macchina, tempo)
(M1,10)
(M2,5)
(M3,6)
J2
(M2,5)
(M1,8)
-
J3
(M1,2)
(M3,10)
(M2,4)
Diagramma di Gantt
Sequenza Operazioni
J1
(M1,10) (M2,5) (M3,6)
J2
(M2,5)
J3
(M1,2) (M3,10) (M2,4)
1
M1
M2
Job
(M1,8)
3
2
-
2
1
3
3
M3
5
10
12
15
1
20
22
26
28
Diagramma di Gantt
M1
Job
Sequenza Operazioni
J1
(M1,10) (M2,5) (M3,6)
J2
(M2,5)
J3
(M1,2) (M3,10) (M2,4)
3
(M1,8)
1
M2
-
2
2
1
3
3
M3
2
5
1
12
17
20 21
23
Classificazione dei problemi di
scheduling
Caratterizzazione dei lavori:
• tempo di processamento pj (pkj)
• data di consegna (duedate o deadline) dj
• data di rilascio (release date) rj
• peso del lavoro (priorità) wj
• tempo di set-up tra due lavori sij
Classificazione dei problemi di
scheduling
Caratterizzazione delle risorse e dell’ambiente
produttivo:
• macchina singola
• macchine parallele
identiche
scorrelate
uniformi
• Flow shop
• Job shop
Macchina singola
LAVORI
M
Macchine parallele
M1
LAVORI
M2
M3
Macchine in linea
(Flow shop)
LAVORI
M1
M2
Mm
Esempio
M1
M2
IN
OUT
Esempio
M1
M2
IN
OUT
Job shop
LAVORI
M2
M1
M3
Misure di prestazione
(lavori)
Dato il lavoro i con release date e duedate:
• tempo di completamento Ci
• tempo di attraversamento Fi= Ci – ri
• Lateness Li= Ci – di
• Tardiness Ti= max{ 0, Ci – di }
• Earliness Ei= max{ 0, di – Ci }
• Lavori in ritardo
Ui= 1 se Ci > di
Ui= 0 se Ci ≤ di
Lateness
(Ritardo)
Ritardo del lavoro i : Li = Ci-di
Li(Ci)
Li > 0
Li < 0
anticipo
di
ritardo
Ci- di
Ci
di: tempo di consegna (duedate) per il lavoro i
Misure di prestazione
(sistema)
• somma dei tempi di completamento: ΣiCi
• flow time totale: Σi Fi
• massima Lateness: Lmax = maxi Li
• massima Tardiness: Tmax = maxi Ti
•Tardiness totale pesata Σi wi Ti
• makespan Cmax = maxi Ci
• numero di lavori in ritardo Σi Ui
Misure di prestazione
Equivalenza tra misure
n
n
Li =
i =1
n
Ci −
i =1
n
di =
i =1
n
Fi +
i =1
i =1
(ri − di )
Misure di prestazione
Una sol. che minimizza Lmax minimizza anche
Tmax (ma, in generale, non è vero il viceversa):
Tmax = max {T1,...,Tn ,0} =
max {max {L1,0},..., max {Ln ,0}} =
= max {L1,..., Ln ,0} = max {Lmax ,0}
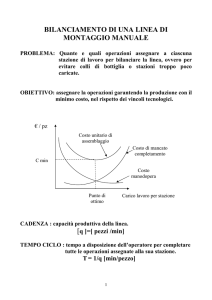
Scheduling su singola macchina
Descrizione del problema
Un insieme di n operazioni deve
essere eseguito su una macchina
Dati
I tempi di processamento pi, i=1,…,n,
del lavoro i sulla macchina sono noti.
Obiettivo
Sequenziare le operazioni sulla
macchina in modo da minimizzare la
somma dei tempi di completamento.
min ΣiCi
Gantt del Sequenziamento
Sequenza S
p1
p2
op1
op2 op3
C1
p3
C2 C3
p4
pn
op4
opn
C4
Cn
Cn=Σi pi: tempo di completamento totale
(makespan)
Obiettivo: min ΣiCi
tempo
se p2 < p1 allora scambiando le op. 1 e 2 si ha
C2< C1 e
C1= C2
C2 + C1 < C2 + C1
S
S’
p1
p2
p3
op1
op2 op3
p4
pn
op4
opn
Cn
C1
C2 C3
p2
p1
p3
p4
pn
op2
op11
op
op3
op4
opn
C2
C1 C3
C4
C4
Cn
tempo
tempo
Regola SPT
(shortest processing time first)
SPT: sequenzia prima le operazioni che hanno
tempo di esecuzione più piccolo
Consente di minimizzare la somma dei tempi di
completamento ΣiCi di n operazioni (lavori) su
una macchina
Esempio
Lavori
1
2
3
4
5
pi
8
16
10
7
2
Sequenza ottima (5, 4, 1, 3, 2)
Scheduling su singola macchina
Descrizione del problema
Un insieme di n operazioni devono
essere eseguiti su una macchina
Dati
I tempi di processamento pi, i=1,…,n,
del lavoro i sulla macchina sono noti.
Peso wi, i=1,…,n, associato ad ogni
lavoro.
Obiettivo
Sequenziare le operazioni sulla
macchina in modo da minimizzare:
min ΣiwiCi
Regola WSPT
(weighted shortest processing time)
WSPT: sequenzia prima i lavori che hanno
il più piccolo rapporto:
pi
wi
Consente di minimizzare la somma pesata
dei tempi di completamento ΣwiCi
Regola WSPT
Sia pi/ wi > pk/ wk consideriamo i due casi:
1. Il lavoro k è sequenziato subito dopo i
C i = A + pi e C k = A + pi + pk
f .ob . = B + w i ( A + p i ) + w k ( A + p i + p k ) + D =
B + (w i + w k ) A + w i p i + w k p i + w k p k + D
2. Il lavoro i è sequenziato subito dopo k
C 'k = A + p k e C 'i = A + p k + p i
f .ob . = B + w k ( A + p k ) + w i ( A + p k + p i ) =
B + (w i + w k ) A + w k p k + w i p k + w i p i + D
Regola WSPT
Se pi/ wi > pk/ wk allora wkpi > wi pk
f .ob .( 1) − f .ob .( 2 ) = w k p i − w i p k > 0
f .ob .( 1) > f .ob .( 2 )
Macchine parallele
M1
J1 J
2
LAVORI
M2
J3 J
4
M3
Scheduling su macchine parallele scorrelate
Descrizione del problema
n lavori devono essere processati da m macchine diverse
(unrelated) disposte parallelo.
Le macchine possono eseguire un solo lavoro alla volta.
Ogni lavoro deve essere eseguito su una ed una sola macchina
senza interruzione.
Dati
I tempi di processamento pij, i=1,…, m, del lavoro j sulla
macchina i sono noti.
Obiettivo
Assegnare i lavori alle macchine in modo tale da minimizzare il
tempo totale di completamento della macchina più carica
(equivalente a minimizzare il makespan).
Esempio
Lavori
Macchine
1
2
3
1
2
3
4
5
12
30
28
17
17
27
19
16
28
15
31
23
14
17
27
Una soluzione ammissibile
M1
J1
M2
J5
M3
J4
J2
J3
34
t
Esempio
Lavori
Macchine
1
2
3
1
2
3
4
5
12
30
28
17
17
27
19
16
28
15
31
23
14
17
27
Una soluzione ottima
M1
M2
M3
J1
J4
J5
J3
J2
33
t
Complessità
Il problema è NP-completo anche con due macchine identiche
• m=2
• pij = p j
i = 1,..., m
Una formulazione di PLI
Definizione delle variabili
Ci , i=1,…, m, tempo di completamento della macchina i
x ij =
1 se il lavoro j è assegnato alla macchina i
0
altrimenti
Cmax = max i =1,...,m {Ci } tempo di completame nto di tutto il sistema
Nota: il tempo di completamento della macchina più carica
corrisponde al tempo di completamento del lavoro che finisce
per ultimo
Formulazione del Problema
Definizione delle variabili
Il tempo di completamento Ci della generica macchina i è pari a:
Ci =
n
j =1
pij x ij
Cmax = max i =1,...,m {Ci } = max i =1,...,m
n
j =1
pij x ij
Una formulazione del Problema
min{Cmax } = min max i =1,...,m
tale che
m
i =1
x ij = 1 j = 1,...,n
x ij ∈ {0,1}
n
j =1
pij x ij
Una formulazione di PLI
min W
tale che
Ci =
m
i =1
n
j =1
pij x ij ≤ W
x ij = 1
xij ∈ {0,1}
i = 1,...,m
j = 1,...,n
ASSEGNAMENTO DELLE
OPERAZIONI DI TAGLIO
NELLA PRODUZIONE DI
CAPI DI ABBIGLIAMENTO
Lo scenario produttivo
• La PAL ZILERI produce capi di
abbigliamento per l’alta moda
• Ogni capo è costituito da vari pezzi
di tessuto (figure)
• Le figure vanno tagliate da un nastro
che scorre a velocità costante v0
Lo scenario produttivo
• La disposizione delle figure sul
nastro è nota a priori (cutting stock
risolto a monte)
• Il taglio delle figure è effettuato da un
insieme di macchine identiche
disposte in linea
• Ciascuna macchina ha un’area di
lavoro di lunghezza Ws
Piazzamento
Lo scenario produttivo
Stazioni di lavoro
figure
•V0 = 12.5 cm/sec
• Ws = 2.5 m
1
2
Ws
Area di lavoro
m
Il problema decisionale
• Il problema è quello di assegnare le figure
•
alle macchine, e di sequenziare i tagli su
ciascuna macchina
Ciascun taglio deve avvenire entro una
determinata finestra temporale (diversa a
seconda della macchina cui è assegnata
la figura) di ampiezza Ws/v0
Il problema decisionale
• Tra il taglio di una figura e la
successiva intercorre un tempo di
switch dipendente dalla sequenza
• Gli obiettivi:
– minimizzare il numero di macchine
– bilanciare i carichi di lavoro
Il problema decisionale
• L’insieme delle figure relative a uno
stesso capo e la loro disposizione sul
tessuto (piazzamento) giungono in
tempo reale
• L’assegnamento va deciso in poco
tempo (30 sec.)
• Problema decisionale on line
Modello combinatorio
6
1
4
2
3
5
6
2
3
6
4
5
4
1
2
6 13
Modello combinatorio
Modello combinatorio
Metodologie di soluzione
• Due approcci risolutivi
• Approccio esatto, basato su metodi
di programmazione a numeri interi
• Approccio euristico, basato su
algoritmi di instradamento push e
pull
Approccio esatto
• Il problema è simile a un problema di
vehicle routing con time windows
• Generalizzazione del problema del
commesso viaggiatore
• Problema difficile
Approccio esatto
•
•
•
•
Sia m l’insieme di tutti i sottoinsiemi di figure
che possono essere tagliati da una sola
macchina entro la propria finestra temporale
(itinerari)
Ad ogni itinerario è associato un dato insieme
di figure da tagliare
xk è una variabile di decisione che è pari a 1 se
l’itinerario k è assegnato ad una macchina
La somma Σk xk esprime il numero di itinerari,
ossia il numero di macchine
Una formulazione di set covering
Sia {1,…, n}
piazzamento.
l’insieme
di
figure
di
un
Sia A = {A1,…,Am} una matrice n × m, in cui la
generica colonna Ak descrive un itinerario
possibile per una macchina. A ha componenti:
ajk=
1 se la figura j è assegnata all’itinerario k
0 altrimenti
Una formulazione di set covering
Sia xk pari a 1 se la colonna Ak è selezionata e 0 altrimenti.
Una formulazione del problema è:
m
min
x
k = 1
m
a
k = 1
x
k
∈
jk
x
k
k
≥ 1
{ 0 ,1 }
j = 1 ,..., n
k
= 1 ,..., m
(Barnhart C. et al., 1994; Chen, Z.L. and Powell,W.B., 1999; Van den Akker
J.M. et al., 1999)
Approccio esatto
•m
è il numero (elevatissimo) di
possibili itinerari
• Anche enumerandoli tutti, occorre
risolvere un problema intero di
elevatissime dimensioni
>>> generazione di colonne
Generazione di Colonne
Primale
m
min
k =1
m
k =1
a
jk
Duale
xk
max
n
j =1
x k ≥ 1 j = 1,...,n
x k ≤ 1 k = 1,...,m
x k ≥ 0 k = 1,...,m
n
j =1
uj
a jk u j ≤ 1 k = 1,...,m
u j ≥ 0 j = 1,...,n
Sia u* la soluzione del problema duale (ristretto).
Un vincolo duale è violato dalla corrente soluzione duale se:
n
j =1
a jk u *j > 1
Un metodo di generazione di colonne
Problema di separazione per generare un vincolo duale violato
dalla corrente soluzione duale
max
n
j =1
a j u *j
tale che
a j ∈ {0 ,1}
le figure scelte ( a j = 1) possono
essere
eseguite
tutte su una macchina
Un metodo di generazione di colonne
Il problema di separazione per generare un vincolo
duale violato e quindi una nuova colonna del primale
è:
1 | r js
w
j
ij
= u
|
w
j
U
j
*
j
Nota che rj e dj sono agreeable (le finestre temporali di
ogni figura sono tutte lunghe Ws/σ), cioè:
r
j
≤ ri ⇔
d
j
≤ d
i
Problema di separazione senza tempi di
set-up (1|rj|ΣwjUj )
Esiste un algoritmo di programmzione dinamica
(Lawler and Moore, 1969) per il risolvere il problema
1||ΣwjUj
Tale algoritmo può essere esteso al problema
1|rj|ΣwjUj se release date e duedate dei lavori sono
agreeable
Un algoritmo di programmazione dinamica
Supponiamo di ordinare i job in modo che d1 ≤ d2 ≤ … ≤ dn (r1 ≤
r2 ≤ … ≤ rn)
Sia P(j, t) la soluzione ottima del problema 1|rj|ΣwjUj in cui sono
considerati solo i primi j job, ed in cui il tempo totale di
completamento dei job in tempo è al più t
{(
P ( j − 1, t ) t < r j + p j
)
}
P ( j , t ) = max P j − 1, t − p j + u *j ; P ( j − 1, t ) r j + p j ≤ t ≤ d j
P j, d j t > d j
(
)
Metodologie di soluzione
Approccio euristico basato su
algoritmi di instradamento push e
pull
Applicazione euristica push
1. Si individua la prossima figura da
assegnare
2. La figura seleziona una macchina
3. La macchina inserisce la figura nel
proprio schedule
push: ordinamento delle figure
• LPT in ordine decrescente di tempo di
taglio
• EDD in ordine di uscita dal sistema
• ERD in ordine di entrata nel sistema
•
•
•
ti istante in cui Mi diviene disponibile
Sij = max{rij, ti + cij}
primo istante in cui può iniziare la
figura j se assegnata a Mi
Qij = Sij - ti (idle)
Earliest start time
per la figura j
Set-up
ti ti+cij
Ultima figura
tagliata
Sij
Idle: Qij = Sij - ti
t
push: selezione della macchina
La figura j corrente sceglie la macchina:
• min Ci che si libera prima
• min Wi con il minimo carico di lavoro
• min Qij che è in grado di tagliare la figura
j col minimo idle
Applicazione euristica pull
1. Si individua la prossima macchina a
cui allocare un lavoro
2. La macchina seleziona una figura
3. La macchina inserisce la figura nel
proprio schedule
pull: ordinamento delle macchine
La macchina che opera la scelta è quella:
• min Ci che si libera prima
pull: selezione della figura
La macchina Mi corrente sceglie la figura,
tra quelle non allocate:
• EDD che uscirà prima dal sistema
• ERD che entrerà prima nel sistema
• min Qij la figura j che è in grado di
tagliare col minimo idle
Inserimento della figura
• In ambedue gli approcci, quando si
determina un accoppiamento
figura/macchina, la figura deve
essere inserita nello schedule
corrente della macchina
Inserimento della figura
• INS1 (EDD) le figure sono tagliate in
ordine di entrata nel sistema
• INS2 (FIFO) le figure sono tagliate
nell’ordine in cui sono state allocate
Euristiche push
Ordinamento
delle figure
Selezione macchina
Inserim.
Push1
LPT
min Wi
EDD
Push2
EDD
min Qij
FIFO
Push3
EDD
min Ci
FIFO
Push4
EDD
min Wi
FIFO
Push5
ERD
min Wi
EDD
Euristiche pull
Ordinamento delle
macchine
Selezione figure
Inserim.
Pull 1
min Ci
EDD
FIFO
Pull 2
min Ci
min Qij
FIFO
Pull 3
min Ci
ERD
FIFO
Indici di performance
E j = D j − (t + p j )
earliness della figura fj
processata sulla
macchina Mk
Emin = min f j ∈B E j
minima earliness del
piazzamento
k
j
E=
f j ∈B
Ej
n
( )
C max = max i =1,..,m Ci
m
earliness media del
piazzamento
tempo di completamento
del piazzamento
numero di macchine
Istanze reali
• Istanza R1: 624 figure raggruppate in
12 piazzamenti
• Istanza R2: 896 figure raggruppate in
16 piazzamenti
Algoritmi push per l’istanza R1
Push1
Push2
Push3
Push4
Push5
Emin
1.7
7
5.9
6.2
1.4
E
10.1
11.7
13.5
11.4
9.8
Cmax
31.5
28.2
28.4
29.2
30.8
m
6
6
6
6
6
Algoritmi pull per l’istanza R1
Pull1
Pull2
Pull3
Emin
6.9
7.4
5.9
E
11.2
15
13.5
Cmax
28.5
29.1
28.3
m
6
7
6
Algoritmi push per l’istanza R2
Push1
Push2
Push3
Push4
Push5
Emin
1.3
6.5
6.2
5.3
0.9
E
10.7
12.4
14.2
12.1
10.4
Cmax
35
29.2
29.3
32.3
34.7
m
7
7
7
7
7
Algoritmi pull per l’istanza R2
Pull1
Pull2
Pull3
Emin
6.3
6.1
6.2
E
11.4
14.3
14.1
Cmax
29
30.1
29.5
m
7
7
7