BILANCIAMENTO DI UNA LINEA DI
MONTAGGIO MANUALE
PROBLEMA: Quante e quali operazioni assegnare a ciascuna
stazione di lavoro per bilanciare la linea, ovvero per
evitare colli di bottiglia o stazioni troppo poco
caricate.
OBIETTIVO: assegnare la operazioni garantendo la produzione con il
minimo costo, nel rispetto dei vincoli tecnologici.
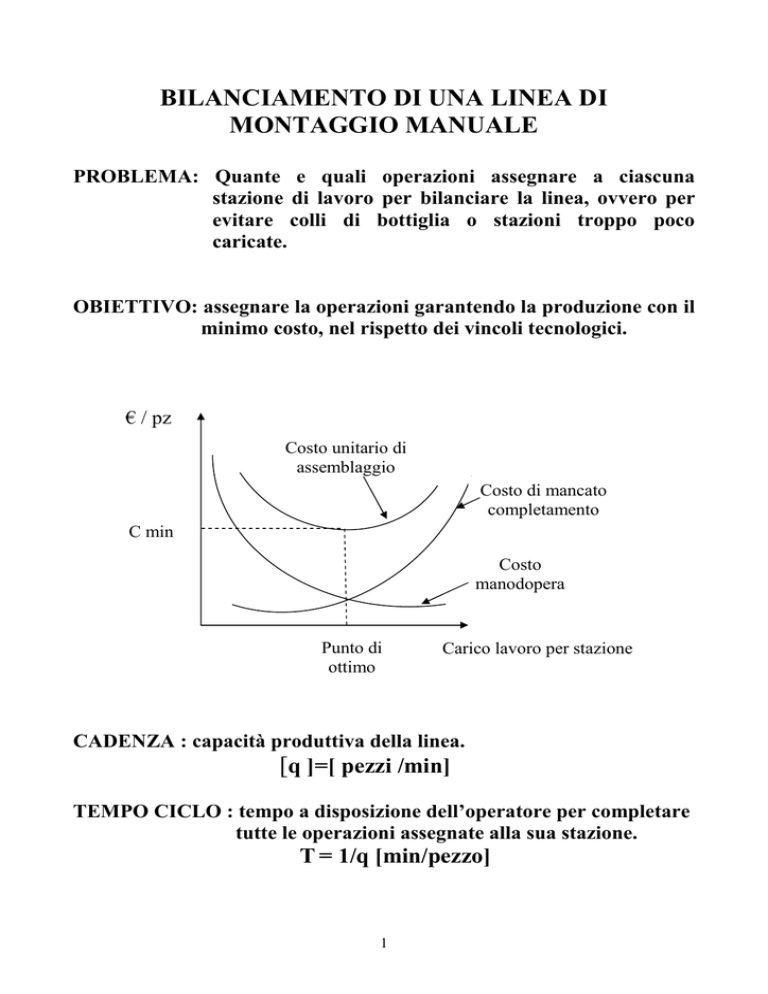
€ / pz
Costo unitario di
assemblaggio
Costo di mancato
completamento
C min
Costo
manodopera
Punto di
ottimo
Carico lavoro per stazione
CADENZA : capacità produttiva della linea.
[q ]=[ pezzi /min]
TEMPO CICLO : tempo a disposizione dell’operatore per completare
tutte le operazioni assegnate alla sua stazione.
T = 1/q [min/pezzo]
1
METODO di KOTTAS-LAU
IPOTESI SEMPLIFICATIVE:
1. Il tempo ciclo e i vincoli di precedenza tra un’operazione e l’altra
costituiscono gli unici vincoli per l’assegnazione dei compiti.
2. Ciascun operatore è retribuito nella stessa misura.
3. Un’operazione può essere iniziata solo se tutte le operazioni con
vincoli di precedenza sono state completate.
4. Il tempo di completamento di ogni operazione è considerato
aleatorio e quindi caratterizzato da una distribuzione normale di
cui si possono calcolare valor medio MK e deviazione standard
σK, la durata di ciascuna operazione è indipendente da quelle
della altre operazioni e dall’ordine con cui sono eseguite.
5. Le operazioni incomplete vanno completate fuori linea; il costo di
completamento fuori linea della singola operazione k-sima I’K
non dipende dalla probabilità di completamento in linea.
Siano:
• T = 1/q = tempo ciclo della linea,
• C = costo orario del lavoro,
• MK, σK = valor medio e deviazione standard della durata della
operazione k-sima,
n
I K = ∑ I 'K
Costo totale di mancato completamento causato
dovuto alla operazione k-sima e a tutte le successive
K =1
• ν = numero operazioni immediatamente successive alla generica
operazione,
•
C
L
M
=
K
K
•
60 (€/unità) = Costo MdO per l’esecuzione della
operazione k-sima
2
Il metodo si basa sulla definizione di: ● Operazioni desiderabili,
• Operazioni sicure,
• Operazioni critiche.
Al fine di definire le tipologie di operazioni precedentemente
introdotte, vengono fatte le seguenti considerazioni:
Se la durata delle operazioni è una variabile aleatoria con
distribuzione normale si può definire:
p(t) = funzione densità di probabilità
p (t)
F(t) = funzione di distribuzione
F (t)
t'
F (t ) = ∫ p(τ )dτ
P (t)
M
0
Probabilità che l’operazione
abbia una durata τ < t’
t’
∞
∞
t'
t'
0
0
P(t ) = ∫ p(τ )dτ = ∫ p(τ )dτ − ∫ p(τ )dτ = 1 − F (t )
P(t) = Probabilità che l’operazione abbia una durata
τ > t’,
cioè che al tempo t’ l’operazione non sia ancora ultimata
p (z)
Variabile normalizzata
F (z)
z=
P (z)
t−M
σ
Valori tabulati
M(z)=0
z’
3
Se alla stazione sono assegnate una serie di operazioni con precisi
vincoli di precedenza, devo considerare l’aleatorietà di tutte le
operazioni precedenti.
zK =
T − ∑j M j
∑σ
j
2
j
Essendo j la generica operazione assegnata alla stazione considerata.
F(zK) = FK =
probabilità che tutte le operazione assegnata alla
stazione, compresa la k-sima siano ultimate entro il
tempo ciclo T.
P(zK) = PK = 1- F(zK) =
probabilità di mancato completamento
della k-sima operazione entro il tempo
ciclo T.
DESIDERABILITA’ MARGINALE
LK ≥ PK ⋅ I K
Costo mancato
completamento
Costo MdO
FK ≥ 1 −
LK
IK
Soglia di desiderabilità:
F ( z K* ) = 1 −
LK
IK
z*K
si ricava dalla tabella
4
Una operazione disponibile all’assegnazione è:
zK
• Operazione DESIDERABILE se
zK
• Operazione SICURA se
≥
≥
z* K ,
z*K = 2,575 (FK ≥ 0,995)
• Operazione CRITICA se non desiderabile quando assegnata ad
una stazione vuota.
L’ASSEGNAZIONE DI UNA OPERAZIONE AD UNA STAZIONE,
NUOVA O GIÀ APERTA VIENE ESEGUITA SECONDO I
CRITERI ESPRESSI DAL DIAGRAMMA DI FLUSSO.
5
ESERCITAZIONE:
Dati preliminari:
- N = numero di operazioni = 11,
- q = 6 unità/ora,
- T = 1/q = 10 min/unità,
- C = 30 €/ora.
Sequenza delle operazioni (diagramma del ciclo di assemblaggio).
2
6
8
10
3
11
1
4
7
9
5
Op.
1
2
3
4
5
6
7
8
9
10
11
Mk σK2
6
2
4
9
2
2
3
6
5
5
3
1,2
0,4
1,0
5
0,4
0,4
0,6
1,2
1,0
1,0
1,8
Nr.Op. Op.
LK
Prec. Succ.
0
2,3,4,5
1
6
1
7
1
7
1
7
1
8
3
9
1
10
1
11
1
11
2
-
6
I’K
3,0
2,0
2,5
7,0
1,5
1,5
2,0
4,0
3,0
3,0
2,0
IK
zK
z*K Pk
PKIK