Strumenti matematici per lo studio delle onde
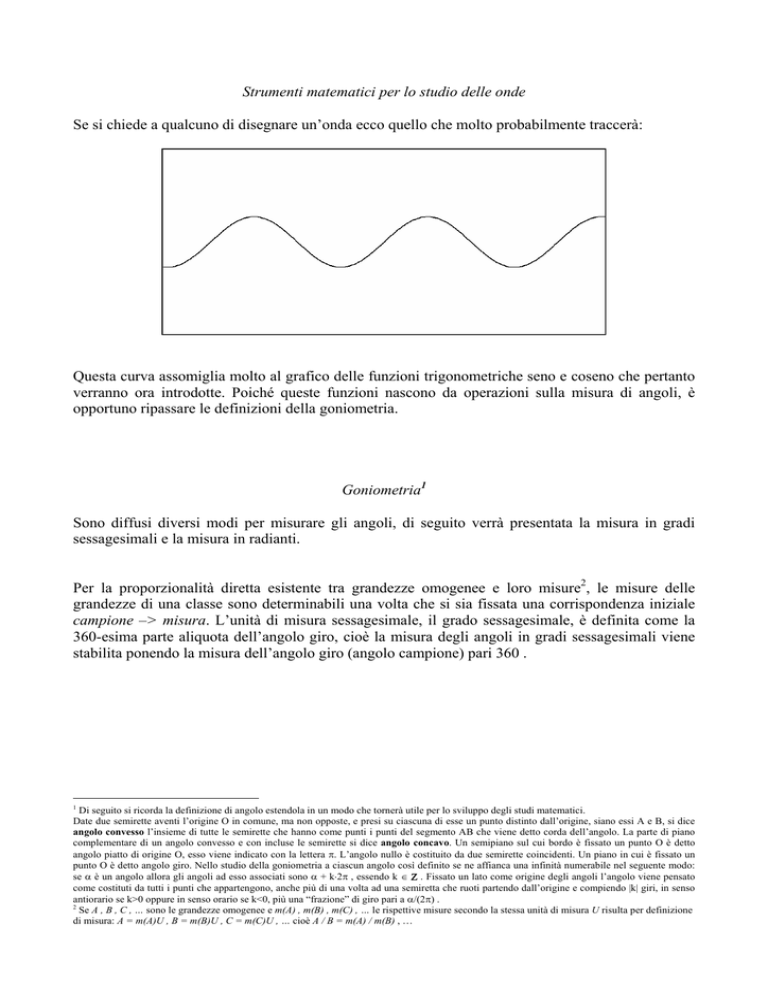
Se si chiede a qualcuno di disegnare un’onda ecco quello che molto probabilmente traccerà:
Questa curva assomiglia molto al grafico delle funzioni trigonometriche seno e coseno che pertanto
verranno ora introdotte. Poiché queste funzioni nascono da operazioni sulla misura di angoli, è
opportuno ripassare le definizioni della goniometria.
Goniometria1
Sono diffusi diversi modi per misurare gli angoli, di seguito verrà presentata la misura in gradi
sessagesimali e la misura in radianti.
Per la proporzionalità diretta esistente tra grandezze omogenee e loro misure2, le misure delle
grandezze di una classe sono determinabili una volta che si sia fissata una corrispondenza iniziale
campione –> misura. L’unità di misura sessagesimale, il grado sessagesimale, è definita come la
360-esima parte aliquota dell’angolo giro, cioè la misura degli angoli in gradi sessagesimali viene
stabilita ponendo la misura dell’angolo giro (angolo campione) pari 360 .
1
Di seguito si ricorda la definizione di angolo estendola in un modo che tornerà utile per lo sviluppo degli studi matematici.
Date due semirette aventi l’origine O in comune, ma non opposte, e presi su ciascuna di esse un punto distinto dall’origine, siano essi A e B, si dice
angolo convesso l’insieme di tutte le semirette che hanno come punti i punti del segmento AB che viene detto corda dell’angolo. La parte di piano
complementare di un angolo convesso e con incluse le semirette si dice angolo concavo. Un semipiano sul cui bordo è fissato un punto O è detto
angolo piatto di origine O, esso viene indicato con la lettera π. L’angolo nullo è costituito da due semirette coincidenti. Un piano in cui è fissato un
punto O è detto angolo giro. Nello studio della goniometria a ciascun angolo così definito se ne affianca una infinità numerabile nel seguente modo:
se α è un angolo allora gli angoli ad esso associati sono α + k⋅2π , essendo k ∈ Ζ . Fissato un lato come origine degli angoli l’angolo viene pensato
come costituti da tutti i punti che appartengono, anche più di una volta ad una semiretta che ruoti partendo dall’origine e compiendo |k| giri, in senso
antiorario se k>0 oppure in senso orario se k<0, più una “frazione” di giro pari a α/(2π) .
2
Se A , B , C , … sono le grandezze omogenee e m(A) , m(B) , m(C) , … le rispettive misure secondo la stessa unità di misura U risulta per definizione
di misura: A = m(A)U , B = m(B)U , C = m(C)U , … cioè A / B = m(A) / m(B) , …
Per definire la misura in radianti di un dato angolo α si considerino le circonferenze aventi
centro nel vertice dell’angolo.
α
Si osserva3 che la classe degli archi l sottesi dall’angolo α è direttamente proporzionale alla classe
dei corrispondenti raggi r : il rapporto l/r è una costante. Essendo l’angolo prefissato l’unico ente
geometrico a rimanere immutato, tale costante può essere usata come misura dell’angolo.
Si dice che la misura di un angolo determinata nel modo appena stabilito è la misura in radianti:
mrad (α ) =
l
r
Il radiante (1 rad = lu/r) ha come campione un angolo al centro di una circonferenza che sottende un
arco lu di lunghezza (misura del segmento rettificante) pari al raggio della circonferenza stessa.
Non sempre è conveniente servirsi del campione dell’unità di misura per misurare le grandezze. Nel
caso della misura in radianti è più semplice servirsi dell’angolo piatto come campione. Per la
definizione data di misura in radianti, la misura dell’angolo piatto (simbolo π) è πr/r = π rad (π , in
questo caso è il simbolo del numero).
nome angolo
Nullo
Angolo al centro del lato dell’icosagono
Metà dell’angolo di un triangolo equiangolo
Angolo del triangolo rettangolo isoscele
Angolo di un triangolo equiangolo
Retto
Piatto
simbolo
0
π/10
π/6
π/4
π/3
π/2
π
Misura (°) Misura (rad)
0
0
18
π/10
30
π/6
45
π/4
60
π/3
90
π/2
180
π
Poiché in goniometria la circonferenza usata per misurare gli angoli in radianti ha raggio unitario4,
la misura in radianti dell’angolo coincide con la misura dell’arco: m(l) ≡ mrad(α) . Per questo
motivo i termini di angolo e di arco sono usati spesso come sinonimi anche se a volte sarebbe
opportuno precisare se si sta parlando della misura di un arco in senso stretto, detta senza ambiguità
misura lineare, o nel senso di angolo, detta senza ambiguità misura angolare; la relazione tra le due
misure è ovviamente la seguente:
se la misura angolare è in radianti:
l = r⋅α ;
se la misura angolare è in gradi sessagesimali:
l = r⋅α⋅π/180 5
Ecco finalmente la procedura da seguire per definire le funzioni coseno, seno e tangente di un
angolo.
3
Per dimostrare tale proporzionalità si deve estendere la definizione di similitudine tra triangoli anche ai settori circolari: si diranno simili due settori
circolari aventi lo stesso angolo al centro, dunque sussiste una proporzione tra gli archi e i corrispondenti raggi. Tale definizione trova fondamento nel
metodo esaustivo che ha portato alla rettificazione della circonferenza: è infatti possibile approssimare, con un errore che può essere reso
arbitrariamente piccolo, i settori “simili” con poligoni simili che li “rettificano”.
4
Il raggio è scelto come campione per definire l’unità di misura delle lunghezze.
5
Si è usata la formula di conversione tra sistemi di unità di misura diverse. Dalla relazione mU’(A) = A/U’ = A/U⋅U/U’ = mU(A)⋅mU’(U) segue che
mU’(A) / mU(A) = mU’(U) , cioè il rapporto tra le misure della stessa grandezza nei due sistemi U’ e U è costante ed uguale al rapporto tra U e U’ cioè
alla misura di U’ rispetto ad U [la costante mU’(U) è detto fattore di conversione dal sistema di U a quello di U’] Quindi mU’(A) / mU(A) = mU’(B) /
mU(B) o anche mU’(A) / mU’(B) = mU(A) / mU(B).
Si consideri in un piano cartesiano ortogonale una circonferenza avente centro nell’origine ed il cui
raggio faccia da unità di misura. Tale circonferenza viene detta goniometrica perché in essa si
riportano gli angoli nel seguente modo: un lato dell’angolo deve coincidere con il semiasse positivo
delle ascisse, mentre l’altro deve essere immaginato come risultante dalla rotazione di una semiretta
che partendo dal semiasse positivo delle ascisse descrive l’ampiezza dell’angolo assegnato (la
rotazione oraria viene attribuita, per convenzione, ai numeri negativi [anche per gli angoli si usa
introdurre quindi una convenzione che associa il verso al segno + o – ) ] .
y
T
y
1
α
O
P
P
sin(α)
x
H
tan(α)
A
α
O
cos(α)
Essendo l’equazione della circonferenza
goniometrica : x2 + y2 = 1 ,
vale:
cos 2 (α ) + sin 2 (α ) = 1
Il punto A(0;1) è detto origine degli archi.
Il punto P(cosα;sinα) è detto estremo d’arco
N.B. In un triangolo rettangolo si ha:
cos(α) = cateto adiacente / ipotenusa
sen(α) = cateto opposto / ipotenusa
tan(α) = cateto opposto / cateto adiacente
H
A
x
Dalla similitudine dei triangoli OHP e OAT
sin(α )
tan(α ) =
⇒
cos(α )
Essendo i termini adiacente e opposto riferiti all’angolo.
nome angolo
simbolo
0
π/10
π/6
Misura
(°)
0
18
30
Misura
(rad)
0
π/10
π/6
Nullo
Angolo al centro del lato dell’icosagono
Metà dell’angolo di un triangolo
equiangolo
Angolo del triangolo rettangolo isoscele
Angolo di un triangolo equiangolo
retto
…
piatto
…
giro
…
π/4
π/3
π/2
…
π
…
2π
…
45
60
90
…
180
…
360
…
π/4
π/3
π/2
…
π
…
2π
…
coseno seno
tangente
1
0
0
√3/2
1/2
√3/3
√2/2
1/2
0
…
–1
…
1
…
√2/2
√3/2
1
…
0
…
0
…
1
√3
∞
…
0
…
0
…
Riportando i risulati del calcolo di coppie (α ; y = cos[α]) su un diagramma si ottiene:
Nel diagramma seguente sono riportati i grafici relativi a diversi valori dei parametri A, k, a che
serviranno per descrivere le onde:











