gli indici di variabilita - FONDAZIONE San Benedetto

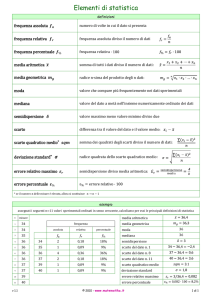
GLI INDICI DI VARIABILITA’
CONSIDERIAMO DUE SEQUENZE DI VALORI CON
MEDIA 47:
12, 24, 32, 43, 56, 74, 88
42, 43, 44, 46, 49, 52, 53

I valori della II serie
sono più vicini alla
media rispetto ai
primi che sono più
sparsi: le due serie
hanno DIVERSA
DISPERSIONE o
VARIABILITA’

QUALI SONO GLI
INDICI DI
VARIABILITA’?
◦ Campo di variazione
◦ Scarto semplice medio
◦ Deviazione standard
IL CAMPO DI VARIAZIONE

È la differenza tra il numero maggiore e
quello minore:
x1  x2  ...  xn
xn  x1
Nel nostro caso:
Sequenza 1:
88 - 12 = 76
Sequenza 2:
53 - 42 = 11
Indice non molto accurato perché tiene conto solo del primo e dell’ultimo
termine e non di quelli intermedi!
Considero due sequenze di numeri con stesso valor medio, 6, e stesso
campo di variazione, 11.
1, 4, 5, 5, 6, 6, 7, 7, 7, 12
1, 1, 1, 1, 2, 10, 10, 11, 11, 12
I valori della seconda sequenza sono comunque più lontani dal 6 di
quelli della prima sequenza.
Per ogni valore calcoliamo lo SCARTO ASSOLUTO DALLA MEDIA,
ovvero la differenza tra il valore e la media in valore assoluto.
S1  1  6  5
S6  6  6  0
S2  4  6  2
S7  7  6  1
S3  5  6  1
S8  7  6  1
S4  5  6  1
S9  7  6  1
S5  6  6  0
S10  12  6  6
LO SCARTO SEMPLICE MEDIO

È la media aritmetica degli scarti:
S
x1  M  x2  M  ...  xn  M
n
Nel nostro caso:
5  2 11 0  0 111 6
S
 1,8
10
5555 4 4 4556
S
 4,8
10
Questo vuol dire che i valori della prima sequenza si discostano mediamente
di 1,8 dalla media, mentre quelli della seconda sequenza sono più lontani dalla
media.
Più accurato e sensibile dello scarto semplice medio è la
DEVIAZIONE STANDARD.
La si usa anche per piccole variazioni nella distribuzione
dei dati intorno alla media.
CONSIDERIAMO: 4, 7, 9, 13, 14, 18, 21, 34.
Media: 15
Calcoliamo gli scarti e li eleviamo al quadrato (SCARTI QUADRATICI):
(4  15) 2  121
(14  15) 2  1
(7  15) 2  64
(18  15) 2  9
(9  15) 2  36
(21  15) 2  36
(13  15) 2  4
(34  15) 2  361
Calcoliamo la VARIANZA,
ovvero la media degli scarti
quadratici.
121  64  36  4  1  9  36  361
 79
8
LA DEVIAZIONE STANDARD

È la radice quadrata della varianza:

x1  M   x2  M 
2
2
 ...  xn  M 
n
È anche detta SCARTO QUADRATICO MEDIO
2