Teoria correlata Leggi dei moti dei pianeti di Keplero La prima legge

Teoria correlata
Leggi dei moti dei pianeti di Keplero
La prima legge di Keplero afferma che le orbite dei pianeti sono ellissi, con il Sole in
un fuoco dell'ellisse. Il Sole non è al centro dell'ellisse, ma in uno dei due fuochi
(generalmente non c'è niente nell'altro fuoco dell'ellisse). Il pianeta segue l'ellisse
nella sua orbita, il che significa che la distanza Terra-Sole cambia costantemente
mentre il pianeta ruota attorno alla sua orbita.
Seconda legge di Keplero: Il raggio vettore che congiunge il pianeta al Sole spazza
aree equivalenti in tempi uguali mentre il pianeta viaggia attorno all'ellisse, quindi il
pianeta si muove più velocemente quando è più vicino al sole. Di conseguenza, un
pianeta compie un moto ellittico con una velocità angolare che cambia
costantemente mentre ruota attorno alla sua orbita. Il punto di minima distanza del
pianeta dal Sole si chiama perielio, il punto di maggiore distanza si chiama afelio.
Dunque, in base alla seconda legge di Keplero, il pianeta si muove più velocemente
quando si trova in perielio e più lentamente quando si trova in afelio.
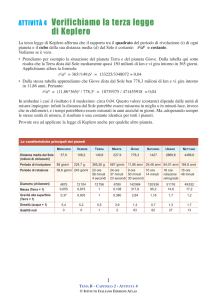
Terza legge di Keplero: I quadrati dei periodi di rivoluzione di due pianeti sono
proporzionali ai cubi dei loro semiassi maggiori:
𝑇1 2
𝑇2 2
=
𝑎1 3
𝑎2 3
n questa equazione T rappresenta il periodo di rivoluzione di un pianeta e a
rappresenta la lunghezza del semiasse maggiore. I pedici "1" e "2" distinguono le
quantità del pianeta 1 e 2 rispettivamente. Si presume che i periodi dei due pianeti
siano nelle stesse unità di tempo e che le lunghezze dei semiassi maggiori dei due
pianeti siano nelle stesse unità di distanza. La terza legge di Keplero implica che il
periodo di rivoluzione di un pianeta intorno al Sole aumenta all'aumentare del raggio
della sua orbita. Di conseguenza, Mercurio, il pianeta più interno, impiega solo 88
giorni nella sua orbita attorno al Sole, mentre Plutone, il pianeta più esterno,
necessita di 248 anni.
Leggi del moto di Newton
La prima legge di Newton afferma che ogni oggetto rimarrà in uno stato di quiete o
di moto uniforme lungo una linea retta, salvo che non sia costretto a cambiare il suo
stato dall'azione di una forza esterna. Questa è la definizione normalmente accettata
di inerzia. Il punto centrale qui è che, se non c'è una forza netta che
agisce sull'oggetto (se tutte le forze esterne si eliminano a vicenda), allora l'oggetto
manterrà una velocità costante. Se quella velocità è zero, allora l'oggetto rimane in
uno stato di quiete. Se si applica una forza esterna, la velocità cambierà a causa di
quella forza.
La seconda legge spiega come la velocità di un oggetto cambia quando è soggetta
a una forza esterna. La legge definisce che una forza è uguale alla quantità di
moto (massa per velocità) per il suo cambiamento nel tempo. Newton ha anche
sviluppato il calcolo matematico e i "cambiamenti" espressi nella seconda legge sono
accuratamente definiti in formule differenziali.
Per un oggetto con massa costante m, la seconda legge afferma che la forza totale F
è il prodotto della massa dell'oggetto e della sua accelerazione a:
F  m  a
Per una forza esterna applicata, il cambio di velocità dipende dalla massa
dell'oggetto.
La terza legge afferma che per ogni azione (forza) in natura c'è una reazione
uguale e una opposta. In altre parole, se un oggetto A esercita una forza su un
oggetto B, allora l'oggetto B esercita una forza uguale sull'oggetto A. Nota che le
forze sono esercitate su oggetti diversi.
Legge di gravitazione universale
Ogni oggetto nell'Universo attrae ogni altro oggetto con una forza diretta lungo la
linea che congiunge i baricentri dei due oggetti che è proporzionale al prodotto delle
loro masse e inversamente proporzionale al quadrato della loro distanza.
𝐅𝐆 = 𝐆
𝐦𝟏 𝐦𝟐
𝐫𝟐
FG è una forza gravitazionale,
m1 e m2 sono le masse dei due oggetti r
è la distanza tra gli oggetti
G
è la costante di gravitazione universale (È chiamata "costante di gravitazione
universale" perché si pensa che sia la stessa in tutti i luoghi e in qualsiasi momento,
caratterizzando l'intrinseca potenza della forza gravitazionale.)
Definizione di forza mareale
Le forze mareali sono determinate della forza di gravità che agisce in punti diversi su
un corpo in movimento. Sono comuni nel sistema solare, causano cambiamenti nei
livelli del mare e influenzano e determinano numerosi processi dinamici che hanno
formato, e tuttora formano, il sistema solare.