Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
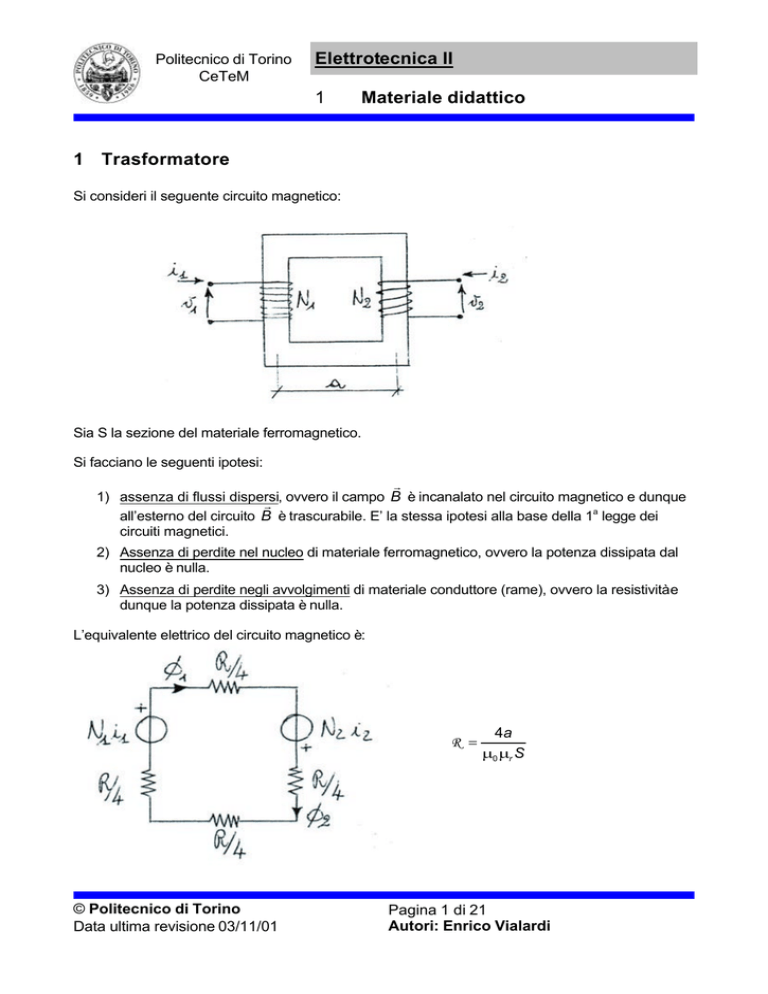
1 Trasformatore
Si consideri il seguente circuito magnetico:
Sia S la sezione del materiale ferromagnetico.
Si facciano le seguenti ipotesi:
r
1) assenza di flussi dispersi, ovvero il campo B è incanalato nel circuito magnetico e dunque
r
all’esterno del circuito B è trascurabile. E’ la stessa ipotesi alla base della 1a legge dei
circuiti magnetici.
2) Assenza di perdite nel nucleo di materiale ferromagnetico, ovvero la potenza dissipata dal
nucleo è nulla.
3) Assenza di perdite negli avvolgimenti di materiale conduttore (rame), ovvero la resistività e
dunque la potenza dissipata è nulla.
L’equivalente elettrico del circuito magnetico è:
R =
© Politecnico di Torino
Data ultima revisione 03/11/01
4a
µ0 µr S
Pagina 1 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
N1i 1 + N2 i 2 N1
N
=
i1 + 2 i2
R
R
R
2
dφ N di
N N di
a) v 1 = N1 1 = 1 1 + 1 2 2
dt
R dt
R dt
2
dφ
N N di
N di
v 2 = N2 2 = 1 2 1 + 2 2
dt
R dt
R dt
φ1 = φ2 = φ =
L1 =
k=
N12
R
M
L1L2
L2 =
= 1⇒
N22
R
M=
N1N2
= L1L2
R
accoppiamento perfetto
Si definisca il rapporto spire n
n=
N1
N2
si ha che:
L1 M
=
M L2
L1
=n
L2
Si scrivano ora le equazioni nel caso di regime sinusoidale permanente
d
→ jω
dt
V1 = jωL1I 1 + jωMI 2
V2 = jωMI1 + jωL2I 2
M
1
V1 = jωL1 I 1 + I 2 = jωL1 I 1 + I 2
L1
n
M
M L2
M
L
I
V2 = jωL2
I1 + jωL2
I 2 = jωL2 I1 + 2 I 2 = jωL2 n I 1 + 2
L2
L2 M
L2
M
n
jωL1 I 1 + I 2
n
V1
L 1 n2
=
= 1 =
=n
V2
I
L
n
n
2
2
jωL2 n I 1 + n
V1 = nV2
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 2 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Si faccia ora l’ulteriore ipotesi:
4) il circuito magnetico è realizzato con materiale ferromagnetico ideale, ovvero
µr → ∞
Ne deriva che:
R =
4a
→0
µ0 µr S
L1 =
N12
→∞
R
Si è detto che:
I
V1 = jωL1 I 1 + 2
n
I1 =
V1
I
− 2
jωL1 n
se L1 → ∞
I1 = −
I2
n
Riassumendo:
V1 = nV2
I
I1 = − 2
n
trasformatore ideale
Il simbolo è:
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 3 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Considerazioni energetiche
1
p(t ) = v 1 (t )i 1 (t ) + v 2 (t )i 2 (t ) = nv 2 (2)− i 2 (t ) + v 2 (t )i 2 (t ) = −v 2 (t )i 2 (t ) + v 2 (t )i 2 (t ) = 0
n
Il trasformatore ideale non dissipa e non immagazzina energia.
Esempio 1
Con riferimento alla figura seguente, si voglia calcolare il rapporto tensione/corrente sulla
porta 1 del trasformatore ideale.
Si ha:
v1
i
= Re
v 2 = −Rc i 2
v 1 = nv 2
i = i1 = −
1
i2
n
v 1 = n(− Rc i2 ) = n 2Rc i1
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 4 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Quindi quando la porta 2 di un trasformatore ideale è chiusa su un resistore di resistenza
Rc , dalla porta 1 si vede un bipolo che è resistore di resistenza equivalente:
Re = n 2Rc
Evidentemente, se le porte invertono il loro ruolo di modo che il resistore Rc chiude la
porta 1, allora alla porta 2 si misura una resistenza di valore
Re =
1
Rc
n2
Esempio 2
Per la rete di figura calcolare:
1. la resistenza del resistore visto dai morsetti A – B
2. determinare inoltre la rappresentazione Thevenin del bipolo indicato nella figura
seguente
Tenendo conto della formula ricavata in precedenza Re =
1
Rc , risulta:
n2
R1 R2 + R3
R5 = Req
+
R
4
2
n
Dalla formula ricavata in precedenza ( Re = n 2Rc ) si deduce la resistenza Thevenin:
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 5 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Re = n 2R
La tensione a vuoto si determina immediatamente tenendo conto che se i1 = 0 anche
i 2 = 0 , in base alla relazione costitutiva del trasformatore ideale; quindi v 2 = e e v 1 = ne .
Ne consegue la rappresentazione Thevenin della figura precedente.
1.1
Utilizzo dei trasformatori nella distribuzione dell’energia elettrica
Senza trasformatori
Rl << Rc
Rl << Rg
La potenza dissipata sulla linea di distribuzione è:
E
(0 )
Pdiss
= 2Rl I 2 = 2R l
R c + R g + 2R l
© Politecnico di Torino
Data ultima revisione 03/11/01
2
E2
≅ 2R l
(Rc + Rg )2
Pagina 6 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Con trasformatori
(0 )
Pdiss
kE
= 2Rl I = 2R l 2
k (Rc + Rg ) + 2Rl
2
2
(0 )
Pdiss
E2
≅ 2Rl 1
= 2
k 2 (Rc + R g )2
k
La potenza dissipata sulla linea di distribuzione si è ridotta di un fattore k 2 con k >> 1.
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 7 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
1.2
Materiale didattico
Esercizio 1
Nel circuito di figura lo stadio di interfaccia che procede il carico è costituito da un
trasformatore ideale. Determinare il rapporto fra il numero di avvolgimenti k = N1
N2
affinché al carico venga trasferita la massima potenza.
[k = 0,436]
1.3
Esercizio 2
Nel circuito di figura determinare:
i rapporti di trasformazione k1, k 2 in modo tale che al carico venga trasferito il massimo
di potenza
la potenza dissipata dal carico nelle condizioni specificate al punto a)
ipotizzando che k1, k 2 siano quelli determinati al punto a) e che il carico venga
rimpiazzato con un resistore da 16 Ω , determinare la potenza dissipata dal carico.
Rs = 50 Ω
Ri = 20 k Ω
R0 = 600 Ω
RL = 4 Ω
α = 800
v s (t ) =
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 8 di 21
Autori: Enrico Vialardi
2
sin(ωt ) V
10
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
a) k1 1
k 2 = 150
20
b) P = 266,67 W
c) P = 170,67 W
1.4
Esercizio 3
Nel circuito in figura il generatore di potenza, rappresentato dal bipolo a destra dei
morsetti A – B, è caratterizzato da una tensione a vuoto sinusoidale di valore efficace
E.
Determinare k ed M in modo che il generatore fornisca alla rete la sua potenza
disponibile
Determinare inoltre quanto vale la sua potenza disponibile.
R1
k =
R
k2
M
=
±
2
ω
C
2
Pdisp = E
2R
© Politecnico di Torino
Data ultima revisione 03/11/01
k2
k 2
2 − L1 2 − L2
ω C
ω C
Pagina 9 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
1.5
Materiale didattico
Modello del trasformatore reale
Si rimuovono ora, ad una ad una, le ipotesi semplificative sotto le quali si è definito il
trasformatore ideale.
Si rimuove innanzitutto l’ipotesi che il materiale ferromagnetico sia ideale, ovvero si
assume µr di valore finito.
Nel dominio del tempo si era scritto:
Rφ = N1i1 + N2 i2
dφ
v 1 = N1
dt
dφ
v 2 = N2 dt
e dunque in regime sinusoidale:
RΦ = N1I 1 + N2 I 2
V
⇒Φ= 1
V1 = jωN1Φ
jωN1
V = jωN Φ
2
2
V2 = jωN 2 Φ = jωN 2
V1
N
V
= 2 V1 = 1
jωN1 N1
n
Ciò significa che la relazione del trasformatore ideale per le tensioni è ancora
rispettata.
RΦ = N1I 1 + N2 I 2
I1 =
I
I
V
I
RΦ N 2
R V1
R
−
I2 =
− 2 =
V1 − 2 = 1 − 2
2
N1 N1
N1 jωN1 n
n
jωL1 n
jωN1
Allora il circuito equivalente diventa:
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 10 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
In modo analogo si può ricavare un altro circuito equivalente:
RΦ = N1I 1 + N2 I 2
I2 =
RΦ N1
−
I
N 2 N2 1
sostituendo
Φ=
V2
jωN2
ed essendo
L2 =
N22
R
I2 =
V2
− nI1
jωL2
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 11 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Si rimuove ora l’ipotesi di assenza di flussi dispersi.
La tensione indotta ai capi degli avvolgimenti
è data dal flusso magnetico Φ incanalato
r
nel circuito magnetico e dal campo B presente nell’aria e creato dalle correnti
impresse dall’esterno. Ovvero:
RΦ = N1I 1 + N2 I 2
V1 = jωN1Φ + jωL1d I 1
V = jωN Φ + jωL I
2
2d 2
2
L1d , L2 d →
induttanza di dispersione
Ponendo V1 ' = V1 − jωL1d I 1 e V2 ' = V2 − jωL2 d I 2
Si ottengono le stesse equazioni ricavate appena sopra.
Allora il circuito equivalente diventa:
Si rimuove ora l’ipotesi dell’assenza di perdite negli avvolgimenti. La resistività del
rame non è dunque nulla, e allora:
RΦ = N1I 1 + N2 I 2
V1 = jωN1Φ + jωL1d I 1 + R1I1
V = jωN Φ + jωL I + R I
2
2d 2
2 2
2
Le resistenze R1 e R2 sono ovviamente in serie rispettivamente a L1d e L2d .
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 12 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Infine, per tenere conto delle perdite nel nucleo ferromagnetico, si inserisca nel
modello una resistenza R0 in parallelo all’induttanza L1 .
Il circuito equivalente del trasformatore reale è pertanto:
Riportando al primario la resistenza e l’induttanza di dispersione dell’avvolgimento
I
secondario ed essendo I1 ≅ − 2 si ottiene il circuito equivalente semplificato del
n
trasformatore reale:
Esso è caratterizzato da quattro parametri:
La resistenza degli avvolgimenti R1 + n 2 R 2
L’induttanza di dispersione L1d + n 2 L2d
L’induttanza dell’avvolgimento primario L1
La resistenza di perdita nel ferro R0
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 13 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
La determinazione di questi parametri avviene sperimentalmente tramite le prove “a
vuoto” e “in cortocircuito”.
1.6
Prova a vuoto
I morsetti del secondario sono in circuito aperto e dunque I 2 = 0 .
I morsetti del primario sono invece collegati ad un generatore di tensione che fornisce il
valore di tensione primaria nominale V1n (ovvero il valore per il quale il trasformatore è
stato progettato e realizzato).
Il voltmetro e il frequenzimetro sono utilizzati per verificare che la tensione applicata
abbia valore efficace e frequenza corrispondenti ai valori nominali.
L’amperometro e il wattmetro misurano rispettivamente la corrente I 1o e la potenza P10
assorbita dal trasformatore in queste condizioni di secondario aperto.
Poiché I 2 = 0 e dunque
I2
= 0 la corrente misurata dall’amperometro è I1 = I 10 .
n
Non essendoci dissipazione di potenza attiva sulla resistenza degli avvolgimenti
R1 + n 2 R 2 , si ha:
P10 = G 0V12n
dove G 0 è la conduttanza del parallelo tra la resistenza R0 e l’induttanza L1 . Ovvero
G0 =
1
R0
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 14 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
da cui:
V12n
R0 =
P10
Inoltre:
Y0 =
1
1
1
j
+
=
−
R0 jωL1 R0 ωL1
1
Y0 =
R0
L1 =
1.7
2
2
1
I
+
= 10
V1n
ωL1
1
I
ω 10
V1n
2
1
−
R0
2
Prova in cortocircuito
I morsetti del primario sono collegati ad un generatore di tensione che fornisce il valore
di tensione primaria necessaria affinché la corrente primaria assuma il suo valore
nominale I 1n . Di conseguenza anche la corrente secondaria assumerà il suo valore
nominale I 2 n .
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 15 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Poiché la tensione primaria da applicare V1cc è molto inferiore al valore nominale V1n ,
la corrente I10 è pressoché nulla e dunque la corrente I 1n scorre nella resistenza
R1 + n 2 R 2 e nell’induttanza L1d + n 2 L2d .
Il wattmetro misura la potenza P1cc assorbita dal trasformatore e dissipata da
R1 + n 2 R 2 , essendo trascurabile la dissipazione di R0 .
(
)
P1cc = R1 + n 2 R2 I 12n
da cui:
R1 + n 2 R2 =
P1cc
I 12n
Inoltre
(
)
(
Z1cc = R1 + n 2 R2 + jω L1d + n 2 L2 d
Z1cc =
V1cc
I 1n
V1cc
=
I 1n
(R
1
L1d + n L2 d
2
1.8
+ n 2 R2
1
=
ω
)
2
(
)
+ ω2 L1d + n 2 L2 d
V1cc
I 1n
2
)
− R1 + n 2 R2
(
2
)
2
Esercizio 4
Le prove a vuoto e in cortocircuito su un trasformatore monofase da 10 kVA, 2200/220
V, 50 Hz hanno dato i seguenti risultati:
prova a vuoto eseguita sul lato bassa tensione
V2 n = 220 V
V1n = 2200 V
I 20 = 2,5 A
P20 = 100 W
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 16 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
prova in cortocircuito eseguita sul lato alta tensione
V1cc = 150 V
I1n =
4,55 A
P1cc = 215 W
Ricavare i parametri del circuito equivalente riferiti rispettivamente al lato bassa
tensione e al lato alta tensione. Ricavare inoltre il rapporto tra la corrente I10 e quella
nominale I 1n , ed infine il fattore di potenza a vuoto e in cortocircuito.
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 17 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
2 Macchine elettriche
Si consideri il seguente circuito magnetico
r
L’andamento della componente radiale del campo B lungo il tra ferro è:
Se invece la forma dell’elemento centrale del circuito magnetico (quello su cui è presente
l’avvolgimento) viene opportunamente sagomata fino ad assumere la struttura di un osso,
ovvero:
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 18 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
r
La componente radiale del campo B lungo il tra ferro assume un andamento sinusoidale
Se l’elemento centrale ruota si genera quello che viene definito campo magnetico rotante,
ovvero in un punto fissato del tra ferro, per esempio ϑ0 , la componente radiale del campo
r
B non è più costante nel tempo, ma ha un andamento sinusoidale:
r
Si era visto che ai capi di una spira, posta in una zona in cui è presente un campo B
variabile nel tempo, si crea una differenza di potenziale uguale alla variazione nel tempo
del flusso magnetico attraverso la superficie della spira stessa.
Ponendo allora una spira sul circuito magnetico considerato (si veda la figura) ai suoi capi
è disponibile una differenza di potenziale.
r
Essendo B sinusoidale lo è anche la differenza di potenziale ai capi della spira.
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 19 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Ciò significa che abbiamo realizzato un generatore di tensione sinusoidale a partire da una
corrente i continua:
La parte di circuito magnetico a forma di osso su cui vi è l’avvolgimento in cui scorre la
corrente i, ovvero la parte di circuito magnetico che ruota, viene chiamata ROTORE.
Viceversa, la parte di circuito magnetico sul quale viene avvolta la spira ai cui capi è
indotta la tensione v è ferma, è solidale con un supporto fisso e viene chiamata
STATORE.
Se, invece di inserire una sola spira sullo statore, ne vengono posizionate tre uguali in
posizione sfasata di 120° l’una dall’altra, si ottengono ai capi delle tre spire tre tensioni
sinusoidali di uguale valore efficace, ma sfasate nel tempo di 120° l’una dall’altra. Si è cioè
realizzato un generatore trifase.
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 20 di 21
Autori: Enrico Vialardi
Politecnico di Torino
CeTeM
Elettrotecnica II
1
Materiale didattico
Si noti che la struttura di rotore (osso di materiale ferromagnetico e avvolgimento percorso
dalla corrente i) altro non è che un elettromagnete.
La struttura realizzata (rotore + statore), sia essa monofase o trifase, è reversibile, ovvero
applicando una tensione sinusoidale alla o alle spire di statore viene generato il campo
r
magnetico rotante B . Il rotore magnetico si comporta come l’ago di una bussola, cioè
cerca di inseguire il campo magnetico rotante. Ciò significa che il rotore ruota. Si è dunque
realizzata una macchina elettrica che trasforma l’energia elettrica in energia meccanica. In
particolare essa viene definita MACCHINA ELETTRICA SINCRONA, perché il rotore ruota
alla stessa velocità del campo magnetico rotante.
Si consideri ora la stessa struttura vista in precedenza, ma anziché alimentare con una
corrente continua i l’avvolgimento di rotore, si chiuda questo avvolgimento in cortocircuito.
Gli avvolgimenti di statore sono identici al caso precedente e dunque creano il campo
magnetico rotante che induce una corrente sinusoidale nell’avvolgimento di rotore.
Detta corrente crea a sua volta un altro campo magnetico rotante, questa volta di rotore.
L’interazione tra il campo magnetico rotante di statore e il campo magnetico rotante di
rotore pone in rotazione il rotore.
Sia Ω c la velocità di rotazione del campo di statore e quella del campo di rotore. Ω r
dipende dalla coppia resistente agente sull’albero della macchina elettrica. Essa non può
però in alcun caso uguagliare Ω c , in quanto se così fosse il campo magnetico di statore
risulterebbe fermo rispetto al campo magnetico di rotore e non potrebbe indurre nessuna
corrente nell’avvolgimento di rotore.
Quindi
Ω r < Ωc
ovvero il rotore deve ruotare più lentamente rispetto al campo di statore. Per questa
ragione una tale struttura viene definita MACCHINA ELETTRICA ASINCRONA.
Per caratterizzare la relazione tra Ω c e Ω r si usa lo scorrimento s:
s=
Ωc − Ω r
Ωc
s =0→
s =1→
0 < s ≤1
sincronismo
rotore bloccato
Valori tipici di s:
2 ÷ 3% nelle macchine di grande potenza
6 ÷ 7% nelle macchine di piccola potenza
© Politecnico di Torino
Data ultima revisione 03/11/01
Pagina 21 di 21
Autori: Enrico Vialardi