Politecnico di Torino
CeTeM
Campi Elettromagnetici II
7
Esercitazioni
Riepilogo su
•
•
•
•
equazioni di Maxwell
vettori complessi e polarizzazione
onde piane
mezzi stratificati
Riferimento: lezioni 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
Testi
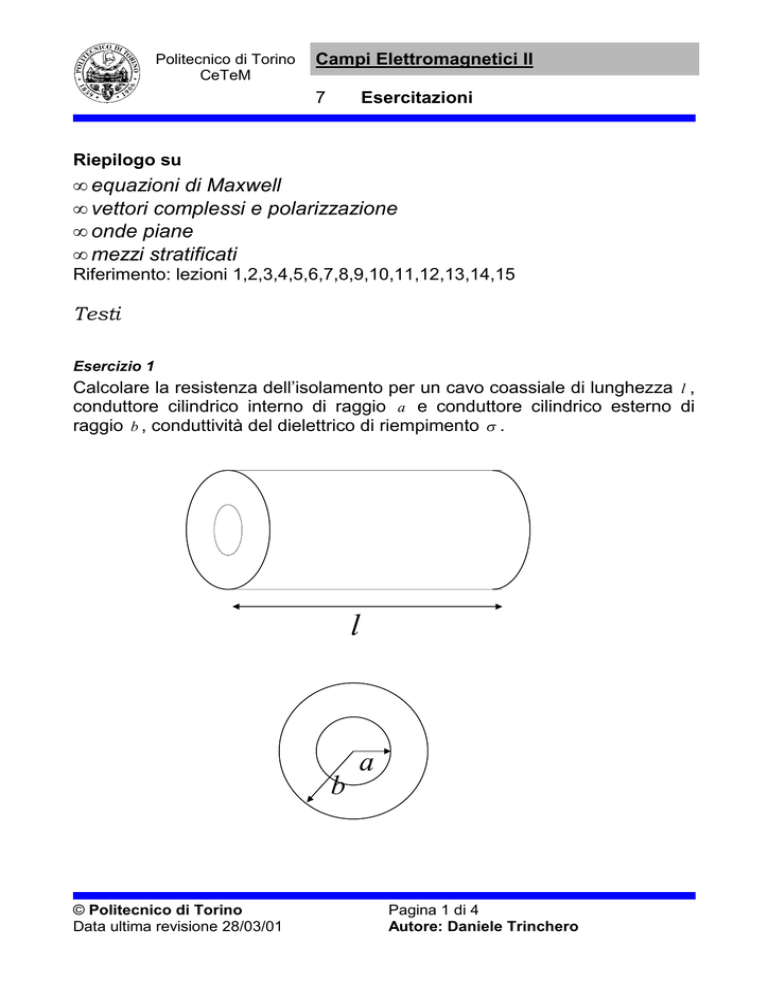
Esercizio 1
Calcolare la resistenza dell’isolamento per un cavo coassiale di lunghezza l ,
conduttore cilindrico interno di raggio a e conduttore cilindrico esterno di
raggio b , conduttività del dielettrico di riempimento σ .
l
b
© Politecnico di Torino
Data ultima revisione 28/03/01
a
Pagina 1 di 4
Autore: Daniele Trinchero
Campi Elettromagnetici II
Politecnico di Torino
CeTeM
7
Esercitazioni
Esercizio 2
Calcolare il modulo della densità di corrente elettrica J e indotta all’interfaccia
dielettrica A della struttura di figura.
Dati: f = 12 GHz , ε r = 1 , ε r = 12 , tg δ = 0.05 , ϑ = 45o , H inc ( 0,0) = H0 y$ , H0 = 0.02 A m .
1
2
x
(1)
H
inc
y
(2)
z
Esercizio 3 (accertamento 09/05/1996 - esercizio 1)
Scrivere l'espressione del fasore E di un'onda piana con polarizzazione
circolare oraria che si propaga nel vuoto lungo l'asse z con E parallelo ad y in
t = T/2, z = 0. Calcolare il campo magnetico istantaneo associato a tale
campo elettrico.
Esercizio 4 (accertamento 09/05/1996 - esercizio 2)
Un'onda piana omogenea nel vuoto ha campo magnetico nel punto O
descritto dal fasore
H (O) = H0 ( jx$ + (1 − 3 j )y$ + 2 z$ )
ed ha fase decrescente lungo +y.
• determinare la direzione di propagazione n e la polarizzazione di H (O)
• calcolare il valore del campo elettrico istantaneo nel punto
6 x$ + 2 y$ − z$
41
all'istante t = 3 4 T .
P = λ0
© Politecnico di Torino
Data ultima revisione 28/03/01
Pagina 2 di 4
Autore: Daniele Trinchero
Campi Elettromagnetici II
Politecnico di Torino
CeTeM
7
Esercitazioni
Esercizio 5 (accertamento 09/05/1996 - esercizio 3)
Un'onda piana omogenea ha campo elettrico nell'origine descritto dal fasore
E = (4 x$ − jy$ + 4 z$ ) . Studiarne la polarizzazione nell'origine. Nel caso di
polarizzazione ellittica, scomporla in due polarizzazioni circolari ruotanti in
verso opposto. Sapendo che tale onda si propaga in un mezzo con piccole
perdite con fase decrescente lungo x ( ε r = 3, tan δ = 0.1) ricavare l'espressione
dei campi elettrico e magnetico nel punto P( 2,2,3) , alla frequenza f = 1GHz .
Esercizio 6 (accertamento 09/05/1996 - esercizio 4)
Sia data un'onda piana che incide sulla struttura di figura. Sapendo che il
campo riflesso nella sezione di discontinuità vale
E rif = Er 0 e − jk 0 (ax − bz ) ( y$ + bx$ + az$ )
calcolare il modulo del campo magnetico totale nell'origine, a sinistra e a
destra della discontinuità.
Dati: ε r = 1 , ε r = 2. 2 , a = 1 2 , Er 0 = 10 −3 V m .
1
2
x
(1)
y
© Politecnico di Torino
Data ultima revisione 28/03/01
(2)
z
Pagina 3 di 4
Autore: Daniele Trinchero
Politecnico di Torino
CeTeM
Campi Elettromagnetici II
7
Esercitazioni
Soluzioni
Esercizio 1
1
b
R=
ln
2πσl a
Esercizio 2
Il campo trasmesso in z = 0 + vale
E t = 4.397 V m
La densità di corrente eccitata sull’interfaccia vale
J = σ E t = 1.76 A
m2
Esercizio 3
E = E0 [− jx$ + y$ ] e − jkz
Esercizio 4
La polarizzazione è ellittica, la direzione di propagazione è data da
n$ =
6 x$ + 2 y$ − z$
41
inoltre
(
)
E P, 3 4 T = Z0
3 x$ + y$ + 20 z$
41
Esercizio 5
La polarizzazione è ellittica.
Scegliendo
x$ + 2 jy$ + z$
2
x$ − 2 jy$ + z$
e$o =
2
e$o =
si ha
E = E o e$o + E a e$a
dove
8− 2
E o = 2
E = 8 + 2
a
2
© Politecnico di Torino
Data ultima revisione 28/03/01
Pagina 4 di 4
Autore: Daniele Trinchero












