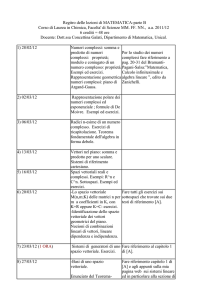
Diario delle lezioni di Matematica Discreta
Anno Accademico 2011/12
Lezione 1 del 03/10/11
Numeri complessi. Forma trigonometrica. Radici n-me dell’unità. Esempi
ed esercizi.
Lezione 2 del 05/10/11
Esercizi sui numeri complessi. Radici n-me di un numero complesso. Radici
di un polinomio.
Lezione 3 del 10/10/11
Spazi vettoriali. Definizione ed esempi. Polinomi a coefficienti in un campo
e spazio vettoriale K n , K campo.
Lezione 4 del 12/10/11
Sottospazi di uno spazio vettoriale. Definizione ed esempi. Sottospazio
generato da un insieme. Combinazioni lineari di vettori.
Lezione 5 del 17/10/11
Vettori linearmente dipendenti e vettori linearmente indipendenti. Esempi.
Basi di uno spazio vettoriale.
Lezione 6 del 19/10/11
Esercizi su sottospazi di uno spazio vettoriale, vettori linearmente dipendenti
e indipendenti, basi.
Lezione 7 del 24/10/11
Basi di uno spazio vettoriale. Esistenza di una base. Proprietà delle basi.
Lezione 8 del 26/10/11
Esercizi. Teorema del completamento a una base.
Lezione 9 del 02/11/12(Radina)
Spazi quoziente e applicazioni lineari.
Lezione 10 del 07/11/11
Nucleo e immagine di una applicazione lineare. Somma di sottospazi. Formula di Grassman.
Lezione 11 del 09/11/11
Esercizi.
Lezione 12 del 14/11/11
Matrici associate ad applicazioni lineari.
Esercitazione del 16/11/11
Esercizi.
Lezione 13 del 5/12/11
Somme dirette. Teorema di nullità più rango.
Lezione 14 del 12/12/11
Matrici. Somma, prodotto per un scalare, prodotto tra matrici, determinante, matrice inversa.
Lezione 16 del 14/12/11
Rango di una matrice. Riduzione a gradino. Esempi e sercizi.
Lezione 17 del 19/12/11
1
2
Sistemi di equazioni lineari. Teorema di Rouchè-Capelli. Eliminazione di
Gauss per i sistemi lineari.
Esercitazione 18 del 19/12/11
Esercizi.
Lezione 19 del 21/12/11
Esercizi.
Lezione 20 del 09/01/12
Regola di Cramer. Autovalori e autovettori. Polinomio caratteristico.
Lezione 21 del 11/01/12
Esercizi.
Lezione 22 del 16/01/12
Endomorfismi diagonalizzabili. Criteri di diagonalizzabilità.