Campo elettrico di un filo infinito carico - Digilander

CAMPO ELETTRICO DI UN FILO INFINITO CARICO
In altri appunti1 è data la dimostrazione di come applicare il Teorema di Gauss (o Legge di Gauss) per
calcolare il campo elettrico in caso di cariche distribuite dentro o su una superficie sferica o disposte su di una
superficie piana infinita.
In questi appunti studieremo come calcolare il campo elettrico prodotto da una carica distribuita lungo un filo
infinito. Utilizzando la Legge di Gauss si dimostra che un filo infinito uniformemente carico produce un
campo elettrico la cui intensità è direttamente proporzionale alla densità lineare di carica ed
inversamente proporzionale alla distanza “r” dal filo.
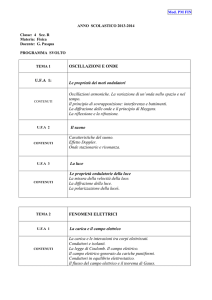
Prendiamo per superficie gaussiana su cui calcolare il flusso un cilindro con
l’asse di simmetria coincidente con il filo (supposto caricato “+”) e le basi
perpendicolari al filo stesso. Supponiamo che il cilindro abbia altezza h e
raggio r. Sperimentalmente si può osservare che le linee di forza sono tutte
semirette perpendicolari al filo uscenti dallo stesso (come possiamo dimostrare
questa proprietà? Cheee?!? Non lo ricordiii?!? E cosa dirai durante la 2a
prova?!? Vai subito a guardare nei tuoi appunti!); ed inoltre il modulo di tutti i
vettori E posti alla solita distanza r dal filo è sempre lo stesso -cioè: a parità di
r il modulo di E non cambia- (questo per motivi di simmetria, anche se ruoto il
filo il campo non si modifica).
Usiamo adesso il Teorema di Gauss (o Legge di Gauss). Sappiamo già che il
flusso totale del campo elettrico () attraverso una superficie chiusa è legato
alla carica elettrica contenuta dentro la superficie (Q) dalla legge1:
 = 4KQ
(1)
Sappiamo anche che il flusso  attraverso una superficie è dato dal prodotto del campo elettrico per l’area
della superficie (A) per il coseno dell’angolo fra il campo elettrico e la normale alla superficie1,2 (angolo ):
= E Acos()
(2)
Per la nostra superficie cilindrica, il flusso totale  è uguale alla somma dei flussi uscenti dalle superfici di base
più quello uscente dalla superficie laterale. Adesso calcoliamo questi flussi:
 Il flusso uscente dalle superfici di base vale 0 essendo 90° l’angolo  che si forma tra la perpendicolare
(chiamata anche normale) alla superficie e la direzione della linea di forza.

Il flusso uscente dalla superficie laterale si può facilmente calcolare se ricordiamo che sulla superficie
⃗ è sempre costante in modulo (perché è sempre alla stessa distanza r dal
cilindrica il campo elettrico 𝐸
filo), ha direzione radiale e verso uscente in ogni punto di essa, come abbiamo già affermato sopra:
indico con E(r) il modulo di ⃗⃗⃗
𝐸 alla distanza r. Inoltre, avendo direzione radiale, 𝐸⃗ è sempre
perpendicolare alla superficie (=0). Applicando l’eq. (2) otteniamo: LateraleE(r)ALateralecos(0°) ;
ALaterale = 2rh  Laterale = E(r)2rh
Da ciò che abbiamo detto, il flusso attraverso la superficie cilindrica coincide con quello laterale:
Laterale = E(r)2rh
(3)
Sostituendo per  l'eq. (1) ottengo: 4KQ = E(r)2rh  𝑬(𝒓) =
𝟐𝑲 𝑸
𝒓 𝒉
.
La frazione Q/h rappresenta la densità lineare di carica e si indica universalmente con λ. Perciò ottengo:
𝑬(𝒓) =
1
2
𝟐𝑲𝝀
𝒓
(𝟒)
Appunti ottenuti rielaborando il testo sul sito:
https://argomentidifisica.wordpress.com/category/potenziale-elettrico/
Negli appunti “Flusso del campo elettrico e legge di Gauss”
Negli appunti “FLUSSO ELETTRICO – una introduzione al Teorema di Gauss”