funzioni reali di una variabile reale - Digilander

FUNZIONI REALI DI UNA VARIABILE REALE
INTERVALLI
Per definire il campo di esistenza (o dominio) di una funzione reale di variabile reale y=f(x)si
devono indicare talvolta insiemi di numeri reali che su una retta orientata e graduata sono
rappresentati dagli infiniti punti di un segmento di dati estremi.
Tali insiemi (di numeri reali o di corrispondenti punti) si dicono intervalli.
Intervallo di estremi a e b (ab) è l’insieme dei numeri reali x   .
Tali intervalli si possono indicare:
INTERVALLI LIMITATI
ab
intervallo aperto
]a,b[
axb
intervallo chiuso [ a , b ]
axb
intervallo chiuso inferiormente aperto superiormente [ a, b[
a  x  b intervallo aperto inferiormente e chiuso superiormente ] a , b ]
INTERVALLI ILLIMITATI
x<c
] -, c[
xc
] -, c]
x>c
]c, +  [
xc
[c, +  [
INTORNO DI UN PUNTO
Ogni intervallo limitato, aperto o chiuso riferito ad un dato punto x0 , in modo che x0 ne sia un punto
interno oppure uno degli estremi, viene chiamato intorno del punto x0.
Quando x0 è interno si dice “completo” e viene chiamato “intorno di x0 “ , quando x0 coincide con
l’estremo inferiore si tratta di intorno destro di x0 , e se x0 coincide con l’estremo superiore si tratta
di intorno sinistro di x0 .
1
FUNZIONI
Date due variabili x e y si dice che la variabile y è funzione della variabile x quando fra le due
variabili esiste una relazione per effetto della quale a ogni valore di x corrisponde un solo
valore per la variabile y.
y= f (x)
x= variabile indipendente
y= variabile dipendente
DOMINIO DI UNA FUNZIONE
E’ l’insieme dei valori che possono essere assegnati alla variabile indipendente x in
corrispondenza dei quali è possibile calcolare il valore della variabile y.
Determinazione del dominio di una funzione:
Funzione razionale intera: è costituito dall’insieme R dei numeri reali
Esempio:
y  5 x 2  3 x  4 dominio :R
Funzione razionale fratta: è costituito dall’insieme R dei numeri reali esclusi quelli che annullano
il denominatore.
3x 2
1
1 
esempio: y=
dominio R/  
2x 1  0 x 
2x  1
2
2 
Funzioni irrazionali:una funzione è irrazionale quando la variabile indipendente x figura anche
sotto il segno di radice.
Se l’indice è pari il radicando deve essere positivo o nullo ed il dominio è costituito da tutti i
numeri reali diversi da quelli che rendono negativo il radicando.
Esempio: y  x  12 deve essere x-12  0
x  12
Quindi il dominio è : x  12 .
Se l’indice è dispari il radicando può essere anche negativo ed il dominio è costituito dall’insieme
dei numeri reali.
Esempio: y  3 x  4 si ha:
dominio: R
Funzione esponenziale: è definita da tutti i valori per i quali è definito l’esponente.
Esempio:
3 x 4
y  4 x 3 deve essere definita la funzione che figura come esponente quindi x≠3
Dominio: R/ 3 
Funzione logaritmica: data una funzione logaritmica y= log a f ( x) (a>0 a≠1) in questo caso
deve essere f(x)>0.
Esempio:
2
y  log( x  12)
dominio: x>12.
deve essere
x-12>0 cioè x>12 quindi:
CODOMINIO DI UNA FUNZIONE
E’ l’insieme dei valori che, in corrispondenza all’insieme dei valori di x, assume la variabile
dipendente y.
test
1) Il Dominio o Campo di Esistenza di una funzione y  f (x) è l’insieme dei valori reali
che possono essere attribuiti:
□ alla x affinché il corrispondente valore reale y non sia nullo
□ alla x affinché la corrispondenza sia biunivoca
□ alla y affinché si possa calcolare la x
□ alla x affinché il criterio per calcolare la y sia effettivamente applicabile
x7
è costituito da:
x ( x  5)
□ l’insieme dei numeri reali diversi da zero
□ tutti i numeri reali
□ l’insieme dei numeri reali maggiori di 5
□ l’insieme dei numeri reali diversi da 0 e da 5
2) Il Campo di Esistenza della funzione y 
3) Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge
che fa corrispondere ad ogni elemento di A:
□ un elemento di B
□ uno ed uno solo elemento di B
□ almeno un elemento di B
□ qualche elemento di B
4) Il dominio della funzione y  ln(5  x ) è:
□ R
□ (5;)
□ (;5)
□ (0;5)
3
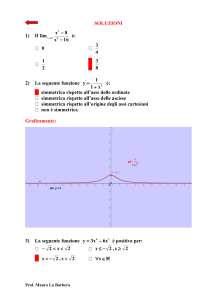
6) Osservare il grafico della funzione y  f (x)
a lato e stabilire quale delle seguenti affermazioni
è vera:
[] il dominio della funzione è R
[] il dominio della funzione è ,2  2,
[] il dominio della funzione è 2,2
[] il dominio della funzione è R  2,2
7)
Il dominio della funzione y  2 x 2  9 x  5 è dato da:
[]  5  x 
[]
1
2
x  5; x 
[] x 
1
2
1
2
[] x  5
8) Il campo di esistenza della funzione f ( x) 
 2
[]  x  9  0
 x  4  0
 2
[]  x  9  0
[]
[]
3
2
3
x
2
x
 2
[]  x  9  0
 x  4  0
9) Il campo di esistenza della funzione y 
ln( x 2  9)
è dato dalle soluzioni del sistema:
x4
 x  4  0
 2
[]  x  9  0
 x  4  0
2x  3
è dato da:
x2
[]
x2
[]
x  2
10)Il dominio della funzione y  ln(5  x ) è:
□ R
□ (5;)
□ (;5)
□ (0,5)
x7
è costituito da:
x ( x  5)
□ l’insieme dei numeri reali diversi da zero
□ tutti i numeri reali
□ l’insieme dei numeri reali maggiori di 5
□ l’insieme dei numeri reali diversi da 0 e da
12) Il Dominio o Campo di Esistenza di una funzione y  f (x) è l’insieme dei valori reali
che possono essere attribuiti:
□ alla x affinché il corrispondente valore reale y non sia nullo
□ alla x affinché la corrispondenza sia biunivoca
□ alla y affinché si possa calcolare la x
□ alla x affinché il criterio per calcolare la y sia effettivamente applicabile
11)Il Campo di Esistenza della funzione y 
4
FUNZIONI CONTINUE
Una funzione f(x) definita in un intervallo [ a, b] si dice continua in un punto x0 di tale
intervallo se esiste finito il lim x x0 f ( x) e tale valore è uguale a quello che la funzione
assume in x0.
F(x) è continua se
lim x x0 f ( x) = f (x0 )
Esempio: si voglia valutare la continuità della funzione di equazione y= x3-1 C.E. =  in x=3
1) si calcola il valore della funzione nel punto 3; f(3)=26
2) si calcola il valore del limite per x che tende a 3
lim x 3 (x3-1 ) = 26
3) confrontare i valori della 1 e della 2
26= 26
la funzione è continua in x=3.
Può capitare che pur potendo calcolare f(x) non sia possibile calcolare il valore del limite per x che
tende a x0 ma che si possa valutare tale limite in un intervallo solo sinistro o destro di x0 .
Se
lim x x0- f ( x) = f (x0 )
la funzione è continua a sinistra del punto x0
se
lim x x0 + f ( x) = f (x0 )
la funzione è continua a destra del punto x0
TEST
1 ) Una funzione è continua in un punto c quando:
[] non esiste il valore della funzione nel punto c, ma esiste il limite della funzione per x  c
[] esiste il valore della funzione nel punto c, ma non esiste il limite della funzione per x  c
[] esiste il valore della funzione nel punto c, esiste il limite della funzione per x  c e il
limite non coincide con il valore della funzione nel punto c
[] esiste il valore della funzione nel punto c, esiste il limite della funzione per x  c e il
limite coincide con il valore della funzione nel punto c
2)Il Dominio o Campo di Esistenza di una funzione y  f (x) è l’insieme dei valori reali
che possono essere attribuiti:
□ alla x affinché il corrispondente valore reale y non sia nullo
□ alla x affinché la corrispondenza sia biunivoca
□ alla y affinché si possa calcolare la x
□ alla x affinché il criterio per calcolare la y sia effettivamente applicabile
5
PUNTI DISCONTINUITA’ PER UNA FUNZIONE
Una funzione non è continua in un punto x0 quando il valore da essa assunta è diverso dal
valore del limite, cioè quando : lim x x0 f ( x)  f (x0 )
si dice che x0 è un punto di discontinuità o punto singolare.
DISCONTINUITA’ DI PRIMA SPECIE
Una funzione definita in un intervallo escluso x0, presenta in x= x0 una discontinuità di prima
specie se esistono e sono diversi i due limiti:
lim x x0- f ( x) = l 1
l1
l2
e
lim x x0 + f ( x) = l 2
la differenza  l 1 - l 2 
è il salto della funzione.
Esempio:
y
2x
il cui dominio prevede che sia x 0
x
Si può quindi considerare il punto x=0 come punto di discontinuità.
Anche se non si può calcolare il valore del suo limite in un intorno completo dello zero si può
calcolare il limite in un intorno destro e in intorno sinistro.
lim x 0+
2x
x
= 2
e
lim x0 -
2x
x
= 2
quindi la funzione non esiste nel punto 0, la funzione fa un salto nel passare da un punto che si
trova a sinistra dello zero ad un punto che si trova a destra.
6
DISCONTINUITA’ DI SECONDA SPECIE
Se si ha ad esempio una funzione y=
si calcola il lim x 2
x2 5
che presenta un punto di discontinuità in x=2
x2
x2 5
= 
x2
Il limite è infinito e si dice che in x=2 la funzione presenta una discontinuità di seconda specie.
Una funzione f(x) definita in un intervallo ecluso il punto x0 , ha una discontinuità di seconda
specie.
In x= x0 se almeno uno dei limiti dalla sinistra o destra è o non esiste.
DISCONTINUITA’ DI TERZA SPECIE
Supponendo di avere la funzione y=
x2  4
ha un punto di discontinuità in x=2.Calcolando il
2x
limite:
lim x 2
x2  4
 ( x  2)( x  2)
= lim x 2
= lim x 2 (x  2) = - 4
2x
 ( 2  x)
Il risultato dimostra che la funzione è discontinua ma che la discontinuità quasi non si vede perché
rimane escluso dal grafico in un solo punto. La discontinuità è eliminabile completando la
definizione così :
y=
x2  4
2x
y = -4
se x 2
se x= 2
una funzione f(x) definita in un intervallo l escluso , presenta in x= x0 una discontinuità di terza
specie o eliminabile se esiste il limite per x che tende a x0 , ma in x0 la funzione non esiste o ha un
valore diverso dal limite.
TEST
1)
Data la funzione f ( x) 
[]
[]
[]
[]
x
x
, il punto di ascissa x  0 :
è un punto di discontinuità di prima specie
è un punto di discontinuità di seconda specie
è un punto di discontinuità di terza specie
non è un punto di discontinuità
7
TEOREMA WEIERSTRASS
Una funzione continua in tutto un intervallo, ha nell’intervallo un valore minimo m e un
valore massimo M.
esiste un punto C la cui ordinata f(C)=m sia non maggiore delle ordinate degli altri punti.
esiste un punto D la cui ordinata f(D)=m sia non minore delle ordinate degli altri punti.
TEOREMA DI BOLZANO
Una funzione continua nell’intervallo [a,b] prende in questo intervallo almeno una volta tutti i
valori compresi fra m e M.
TEOREMA DELL’ESISTENZA DEGLI ZERI
Se agli estremi dell’intervallo di definizione [a,b] una funzione continua assume valori di segno
contrario, vi è almeno un punto compreso fra a e b nel quale la funzione si annulla.
8
TEOREMA PERMANENZA DEL SEGNO
Se in un punto c interno all’intervallo [a,b] di definizione, la funzione continua f(x) assume
valore diverso da zero, esiste un conveniente intorno I di c, nel quale la funzine ha lo stesso
segno che ha in c. Se :
lim x c f ( x) = l  0 esiste un intorno I di c, tale che in questo intorno, f(x) ha lo stesso
segno di l.
9
ASINTOTI DI UNA FUNZIONE
ASINTOTO VERTICALE
lim x x0 - f ( x) = +  oppure lim x x0 + f ( x) = + 
verticale per la funzione.
Se
ESEMPIO:
y=
3x 2
2x  1
se lim x ½-
C.E. 2x-10
3x 2
=-
2X  1
la retta x= ½
x  1 /2
2x1
oppure
lim x½+
3x 2
=+
2X  1
è un asintoto verticale .
10
la retta x= x0 è un asintoto
ASINTOTO ORIZZONTALE
Se
lim x+ f ( x) = l oppure lim x- f ( x) = l
la retta y= l è un asintoto orizzontale per la funzione f(x)
esempio:
y=
3x  1
x 1
3x  1  H
  lim x+
x 1 
y=3 asintoto orizzontale
lim x+
3/1=3
ASINTOTO OBLIQUO
Può capitare però che una curva, per x tendente all’infinito si avvicini ad una retta che non
sia parallela all’asse delle ascisse ma obliqua, se tale retta esiste si dice asintoto obliquo per la
curva
Se lim x+ f ( x) =  oppure lim x- f ( x)=  non vi sono né asintoti orizzontali né
asintoti verticali, possono esserci asintoti obliqui, cioè rette di equazione y = mx+q.
Si dice che y = mx+q è un asintoto obliquo se :
lim x+ [f ( x)-(mx+q)] = 0 oppure lim x-[f ( x)-(mx+q)] = 0
11
pertanto se la retta y=mx+q è un asintoto obliquo esistono i limiti
m = lim x+ f ( x)/x
oppure:
e
q = lim x+ [f ( x)- mx]
m = lim x- f ( x)/x
e
q = lim x- [f ( x)- mx]
ESEMPIO:
y=
3x 2
2x  1
C.E. 2x-10
se lim x +
3x 2
=+
2X  1
2x1
oppure
x  1 /2
lim x-
3x 2
=-
2X  1
potrebbero esistere asintoti obliqui.
3x 2
3x
m = lim x+
/ x = lim x+
= 
2x  1
2x  1
e
q = lim x+ [-
= =
H
lim x+
=
H
lim x+
3
3
=
2
2
3x 2 3
6 x 2  3x(2 x  1)
3x
- x] = lim x+
= lim x+
=
2x  1 2
4x  2
4x  2
3
3
=
4
4
l’asintoto obliquo ha equazione y =
3
3
x +
2
4
12
TEST
1)
La funzione f ( x) 
2 x 3  3x  5
ammette:
x2  9
[] due asintoti verticali di equazioni x  3 e x  3 ed uno obliquo di equazione y  2 x ;
[] un asintoto verticale di equazione x  3 ed uno orizzontale di equazione y  2 ;
[] due asintoti verticali di equazioni x  3 e x  3 ed uno orizzontale di equazione y  2 ;
[] un asintoto verticale di equazione x  3 ed uno orizzontale di equazione y  2 ;
2)La funzione f ( x) 
x 2  2x  4
è rappresentata dal grafico seguente:
x
Gli asintoti della funzione sopra descritta sono le rette rappresentate dalle equazioni:
[] x  0 e y  2 x  2 ;
[] x  1 e y  x  2 ;
[] x  0 e y  x  2 ;
[] x  0 e y  x  2 ;
3) Se lim f ( x )   la retta x  6 , per il grafico della funzione y  f (x) è:
x 6
[] un asintoto obliquo
[] una retta tangente
[] un asintoto orizzontale
[] un asintoto verticale
4) Indicare la funzione che possiede un asintoto obliquo:
[]
[]
5)
y
x 1
[]
2
2 x  5x  2
y
2 x 2  5x  2
x 1
La funzione y 
[]
y
y
La funzione y 
2 x 2  5x  2
x 3 1
[] ha asintoto obliquo
[] ha come asintoto la retta y  3
3x 2  6 x  3
x2  4
[] ha come asintoti le rette y  3 e x  2
[] non ha asintoti
7)
x2 2
3x 2  6 x  3
x2  4
[] ha come asintoti le rette y  3 e x  2
[] non ha asintoti
6)
2 x 2  4x  1
[] ha asintoto obliquo
[] ha come asintoto la retta y  3
La retta y  1 rappresenta un asintoto orizzontale per la funzione:
13
[]
y
[]
y
x2
x 2 1
1 x2
x 2 1
8)La funzione y 
y  1
y0
[]
[]
[]
y
[]
y
x2 4
x 1
1 x 2
x 2 1
ex
ammette un asintoto orizzontale per x   . Quale ?
1 x
[] y  1
[] y  2


Considera la funzione f ( x)  ln 4  x 2 ; essa:
non ammette asintoti
ammette due asintoti verticali x  2; x  2
ammette un asintoto orizzontale y  0
ammette un asintoto obliquo y  x  1
9)
[]
[]
[]
[]
10) Se risulta che lim f ( x )   allora:
x 
la curva y  f (x) può presentare asintoti obliqui [] la curva y  f (x) non presenta asintoti
la curva y  f (x) non presenta asintoti obliqui
[] la curva y  f (x) ha un asintoto obliquo
[]
[]
11)
Se risulta che lim f ( x)   e lim
x
x 
f (x)
 2 allora:
x
[] nulla si può dire sull’esistenza dell’asintoto obliquo
[] la curva y  f (x) presenta un asintoto obliquo con coeff. angolare m  2
[] la curva y  f (x) non presenta asintoti obliqui
[] la curva y  f (x) ha un asintoto obliquo di equazione y  2 x
12)La retta y  3 è un asintoto orizzontale per la funzione:
□ y
6x 2  3
2x
□ y
3x 3  2 x  1
3
□ y
x  2x 1
□ y
2x 2  3
14
x3  2
x 2 1
x 2 1
DERIVATE
Sia f(x) una funzione definita in un intervallo [a,b] e sia x0 un punto interno ad esso. Detto x un
punto di [a,b] distinto da x0 si dice incremento della variabile x e si indica con ∆x la
differenza: ∆x= x- x0 . questa differenza si può indicare con h
h= x - x0
Risulta x= x0 + h
e ∆x=h da cui essendo x≠ x0 si ha h≠0
Siccome la funzione f(x) è definita in [a,b] ad x0 corrisponde f (x0 ) e ad x0 +h corrisponde
f(x0 +h) e pertanto si dice incremento della funzione relativo all’incremento ∆x=h della
variabile x, e si indica con ∆f la differenza:
∆f = f(x0 +h)- f (x0 )
Si definisce rapporto incrementale :
f ( x 0  h)  f ( x 0 )
f

x
h
Definizione
Si definisce derivata di una funzione f(x) nel punto x0 il limite quando esiste ed è finito, del
rapporto incrementale, al tendere a zero dell’incremento h della variabile:
lim h 0 =
f ( x0  h)  f ( x 0 )
h
SIGNIFICATO GEOMETRICO DI DERIVATA
Si consideri la funzione f(x), sia P un generico punto di ascissa x e ordinata f(x) e Q un altro suo
punto di ascissa x+h e ordinata f (x+h) .
Quando Q percorre la curva avvicinandosi indefinitamente a P, la retta PQ assume la posizione
limite che diremo tangente in P.
dal triangolo PQR si ha :
15
tang = QR/PR=
f ( x  h)  f ( x )
h
quando h tende a zero, Q tende a P, e la secante tende alla tangente t in P , di coefficiente
angolare tang  quindi:
f ( x  h)  f ( x )
tang  = lim h 0 tang  = lim h 0
h
tang  = f ’(x)
Il coefficiente angolare della tangente ad una linea di equazione y= f(x) in un suo punto, è
uguale alla derivata di f(x) in quel punto.
DERIVATE DI ALCUNE FUNZIONI ELEMENTARI
y =costante
y’=0
y= xn
y’= n x n-1
y=x
y’=1
y= 1/x
y’= - 1/x2
y=n√x
y’= 1/ n n√xn-1
y= sen x
y’= cosx
y= cos x
y’= -senx
y= tg x
y’= 1/ cos2x= 1 + tg2x
y= ctgx
y’=- 1/ sen2x=-( 1 + ctg2x)
y= ln x
y’= 1/x
y= ex
y’= ex
REGOLE DI DERIVAZIONE
DERIVATA DEL PRODOTTO DI UNA FUNZIONE PER UNA COSTANTE
y= K f(x)
esempio
y= 4x5
y’= k f’(x)
y’ = 20 x4
DERIVATA DI UNA SOMMA DI FUNZIONI
y= f (x) + g (x)
esempio :
y= 3 x2 +7x+6
y’= f ’ (x) + g’ (x)
y’= 6x+7
16
DERIVATA DEL PRODOTTO DI DUE FUNZIONI
y = f (x) . g (x)
esempio :
y’= f ’ (x). g(x) + g’ (x).f(x)
y=(4x2+1) .( 2x+3)
y’= 8x.(2x+3) + 2. (4x2+1)= 16x2+24x+ 8x2+2= 24x2+24x++2
DERIVATA DEL QUOTO DI DUE FUNZIONI
y= f(x)/g(x)
f ’ (x). g(x) - g’ (x).f(x)
______________
[g(x)]2
y’=
esempio:
3x+1
______
x-2
3(x-2)-(3x+1)
y’=_________________=
(x-2)2
y=
-7
_________
(x-2)2
DERIVATA DI FUNZIONE DI FUNZIONE ( O DERIVATA COMPOSTA)
La derivata di una funzione di funzione è uguale al prodotto della derivata che si ottiene
considerando come variabile la funzione da cui essa dipende per la derivata di tale funzione.
y= F[f(x)]
y’=F’[f(x)].f’(x)
ESEMPIO
y= log(x2+1)
y’=2x/ (x2+1)
DERIVATE DI ORDINE SUPERIORE
Si è visto che una funzione ha per derivata un’altra funzione,applicando il procedimento di
derivazione a quest’ultima si ottiene una nuova funzione che si chiama derivata seconda y’’;
da questa per successiva derivazione un’altra funzione che si dirà derivata terza y’’’ e così di
seguito.
ESEMPIO:
y= ( x5-4x3-2)
y’=(5x4 -12 x2)
y’’=(20x3 -24x)
y’’’=(60x2 -24)
lv
v
y =(120x )
y =(120 )
yvl=0
TEST
1)La derivata prima della funzione y 
□ y' 
2x 3  1
2x 2
x 3 1
è
2x
□ y' 
3
□
y' 
x 2
x2
□ y' 
3)La derivata prima della funzione y 
2x 3  1
2x 2
4x 3  2
2x 2
3x 2  2
x2 1
è
17
6x
□ y' 
2
( x  1)
□
y' 
□ y' 
2
12 x 3  10 x
2
( x  1)
□ y' 
2
2x
2
( x  1) 2
6x
2x
4)La derivata prima della funzione y  x  sen5 x è
□ y '  1  cos 5 x
□ y '  1  cos 5 x
□ y '  sen5 x  5 x cos 5 x
□ y '  1  5 x cos 5 x
5)La derivata prima della funzione y  x  sen5 x è
□ y '  1  cos 5 x
□ y '  1  cos 5 x
□ y '  sen5 x  5 x cos 5 x
□ y '  1  5 x cos 5 x
5) Data la seguente funzione f ( x)  3x 2  6 x  4 la derivata nel punto x  1 vale :
[] 0
[] -5
[] 13
[] -12
7) La derivata della funzione y 
[]
y' 
[]
y' 
1 x 2
4  x2
1 x
è:
y' 
[]
4  x 
2 2
6x
5x
x4
[]
4  x 
2 2
y' 
1
4 x
LIMITI DI FORME INDETERMINATE .TEOREMA DI
DE L’HOPITAL
Per il calcolo dei limiti che si presentano sotto forma indeterminata:
,
0/0,
0.,
-,
1 ,
00 ,
0
è di valido aiuto il teorema di DE L’HOPITAL:
Se due funzioni continue f(x) e g(x) tendono a zero per x tendente ad a, il limite del loro
rapporto è uguale al limite del rapporto delle derivate, se quest’ultimo esiste.
Il teorema sussiste anche nel caso che f(x) e g(x) tendano a infinito per x tendente ad a
oppure ad .
TEST
1) Applicando il Teorema di De l’Hopital al
[]
[]
2
3
0
lim
x  
2x  4

ln 3x 2  5
 si ottiene:
4
5
[] 
[]
2) Il valore del lim
x  
2x  4
x 2  16
è:
□ 0
□ 
18
□ 
□ 5
2
3) Il valore del lim
x 3
x  5x  6
x2  9
è:
□ 0
1
□
6
□ 
2
□ 
3
4) Considera il lim
x 
3x 2  5x  1
4 x 2  5x  1
; esso:
0
3
ma vale
0
4
0
assume la forma indeterminata
ma vale 
0
2x
Il lim
vale:
x   4  3 x 2
1

[]
2
0
[] 3
[] assume la forma indeterminata
[]
5)
[]
[]
6) Il valore del
[] 
lim
x  

3
ma vale

4

4
[] assume la forma indeterminata
ma vale

3
[] assume la forma indeterminata
x 1
è:
3x  2
[] 0
3
3
7) Quale delle seguenti frazioni rappresenta una forma indeterminata:
0
0
[]
[]
n
0
n
n
[]
[]

0
[]
3
[]
STUDIO FUNZIONE
FUNZIONI CRESCENTI E FUNZIONI DECRESCENTI IN UN DATO
INTERVALLO
FUNZIONI CRESCENTI Si dice che una funzione y=f(x) definita in un certo intervallo,
è crescente in quel intervallo se per ogni coppia dei valori x1 e x2
f(x1)<f(x2)
19
con x1<x2 risulta
FUNZIONI DECRESCENTI Si dice che una funzione y=f(x) definita in un certo
intervallo, è decrescente in quel intervallo se per ogni coppia dei valori x1 e x2 con x1<x2
risulta f(x1)>f(x2)
FUNZIONI CRESCENTI E FUNZIONI DECRESCENTI IN UN PUNTO X0
FUNZIONE CRESCENTE
Una funzione f(x) è crescente in un punto x0 se è possibile fissare un intorno completo
di x0 tale che essendo x0+h un punto qualsiasi dell’intorno risulta:
f(x0 + h) –f(x0)
>0 se h>0
oppure
<0 se h<0
f(xo+h)-f(xo)<o oppure f(xo+h)-f(xo)>o
h<0
h>0
FUNZIONE DECRESCENTE
Una funzione f(x) è decrescente in un punto x0 se è possibile fissare un intorno completo
di x0 tale che essendo x0+h un punto qualsiasi dell’intorno risulta:
f(x0 + h) –f(x0)
<0 se h>0
oppure
>0 se h<0
f(xo+h)-f(xo)>o oppure f(xo+h)-f(xo)<o
h<0
h>0
20
TEOREMA
Consideriamo una funzione y=f(x) derivabile in un punto x0 se la sua derivata prima in x0
è positiva la funzione è crescente in x0 , se la sua derivata prima in x0 è negativa la
funzione è decrescente in x0.
Tenendo presente il significato geometrico di derivata di una funzione in un punto : f’(x0 )
fornisce il coefficiente angolare della retta tangente alla curva f(x) nel punto x0.
funzioni crescenti:
funzioni decrescenti:
sia che la funzione sia concava verso l’alto o verso il basso.
Esempio.
Trovare l’intervallo in cui la seguente funzione è crescente o decrescente:
y  2 x 3  15 x 2  24 x  3
Si calcola derivata prima: y '  6 x 2  30 x  24
Trovo le due soluzioni di 6 x 2  30 x  24  0 che sono x=1 e x=4
y'  0
  0 concorde è verificata per valori esterni al valore delle soluzioni
y'  0
  0 discorde è verificata per valori interni al valore delle soluzioni
In conclusione la funzione è crescente in (  ,1) (4,+ ) ; decrescente in ( 1;4).
21
x<1 x>4
1<x<4
TEST
1) Nella figura è rappresentata la funzione
y  2 x 3  3 x ; in quale tra gli intervalli
proposti la funzione risulta decrescente ?
2
2
;x
2
2
[] 1  x  1
[] x  0
[] x  
[] 
2
2
x
2
2
2)Determina in quali intervalli la funzione y  x 3  2 x 2  x è crescente e in quali è decrescente:
1
1
e per x  1 è crescente; per  x  1 è decrescente
3
3
[] è sempre crescente
1
1
[] è crescente per  x  1 ; è decrescente per x 
e per x  1
3
3
[] è crescente per x  1 e decrescente per x  1
x 1
3)La funzione y 
risulta crescente per :
x 1
□ x  1; x  1
□ sempre
□ x0
□ mai
2
4) La funzione f ( x)  x è crescente per:
[] x  1
[] x  1
[] x  1
[]
x0
[]
5)
per x 

2
2
[] 6 x  18 x  7
[] 6 x  18
6)
[] 18 x  7  6 x
[] 7  18x 2  6 x


La derivata della funzione y  2 x 2  3x  1


34 x  32 x  3x  1
[] 24 x  3 2 x 2  3
[]

La derivata della funzione y  2 x  3 x 2  3x  1 è:
2
2
2

3
è:

[] 4 x  3 2 x 2  3x  1

2

[] 2 x  3 x  1
2
22
MASSIMI E MINIMI RELATIVI
Sia f(x) una funzione reale definita nell’intervallo [a,b] e xo un punto di questo intervallo.
Se esiste un intorno H  [a,b] del punto xo , per ogni xxo risulta:
f(x) f(xo)
f(x) f(xo)
si dice che xo è un punto di massimo relativo
si dice che xo è un punto di minimo relativo
DETERMINARE MASSIMI E MINIMI RELATIVI
Esempio 1
Data la funzione y= x3-12x+4
1) si calcola derivata prima y’= 3 x2 -12
2) si pone y’=0
3x2-12=0
risolvendo si ottiene
x1= -2
x2  2
3) si calcola derivata seconda:
y’’=6x
Per x=-2
y’’(-2)=-12 <0
per x=2
y’’(2)=12= >0
massimo relativo in x=-2
minimo relativo in x=2
y’’(0)=0
non si può dire nulla sulla natura del punto x=0
4)si calcola ordinata del massimo e minimo relativo:
y(-2)=(-2)3-12(-2)+4=20
y(2)= 23-12.2+4=-12
max rel. (-2;20)
min.rel. (2;-12)
Esempio 2
Data la funzione y= 2x5+5x4-10x3+4
1) si calcola derivata prima y’= 10 x4 + 20x3 – 30 x2= 10 x2 (x2+ 2x-3)
4) si pone y’=0
x2 =0
x2+ 2x-3=0
x1=-3
x2=0
3) si calcola derivata seconda
x3=1
y’’=40x +60x2-60x = 20x.(2x2+3x-3)
3
23
y’’(-3)=-360<0
massimo relativo in x=-3
y’’(1)=40 >0
minimo relativo in x=1
y’’(0)=0
non si può dire nulla sulla natura del punto x=0
5) si calcola la derivata terza
y’’’= 120 x2+120x-60
y’’’(0)=-60
poiché la prima derivata che non si annulla nel punto xo=0 è di ordine dispari il punto ‘0’
non è di massimo né di minimo.
Esempio3
Data la funzione y= x6-6x4+4
1) si calcola derivata prima y’= 6x5 -24 x3 = 6x3 (x2-4)
6) si pone y’=0
6x3 =0
x2-4=0
x1=0
x2=-2
3) si calcola derivata seconda
x3=2
y’’=30x4-72x2 = 6x2.(5x2-12)
y’’(-2)=24.(20-12)>0
minimo relativo in x=-2
y’’(2)=24(20-12) >0
minimo relativo in x=2
y’’(0)=0
non si può dire nulla sulla natura del punto x=0
4)si calcola la derivata terza
y’’’= 120 x3-144x
y’’’(0)=0
7) si calcola la derivata quarta
yIV=360x2-144
questa risulta negativa per x=0
yIV(0)= -144 <0
siccome la prima derivata che non si annulla è di ordine pari
il punto (0;34) è un punto di massimo relativo.
1)La funzione y  x 3  2 x 2  7 x ha :
□ un massimo per x  
7
3
□ né massimo né minimo
□ un minimo per x  0
□ un massimo per x  1 e un minimo per x  1
24
2)Se in x  x 0 la funzione y  f (x) ha un minimo relativo allora:
□ f ' ( x0 )  0 e f ' ' ( x 0 )  0
□ f ' ( x0 )  0 e f ' ' ( x 0 )  0
□ f ' ( x0 )  0 e f ' ' ( x 0 )  0
□ f ' ( x0 )  0 e f ' ' ( x 0 )  0
3) La funzione y  x 3  2 x 2  7 x ha :
□ un massimo per x  
7
3
□ né massimo né minimo
□ un minimo per x  0
□ un massimo per x  1 e un minimo per x  1
x
4) La funzione y 
è:
x 1
□ ha un massimo in x  1
□ ha un massimo in x  0
□ ha un minimo in x  0
□ non presenta né massimi né minimi
5)Individuare tra i seguenti gli eventuali punti di massimo e di minimo relativo per la
curva di equazione y 
[]
[]
[]
6)
x2 9
:
x 2 1
P 0;9 massimo relativo; Q 3;0 minimo relativo; R 3;0 minimo relativo
P 0;9 minimo relativo; Q 3;3 massimo relativo
P 0;9 minimo relativo e non esistono massimi relativi
[] non esistono né minimi né massimi relativi
x 2  10 x  21
ammette:
2 x  15
[] un massimo M 6;1 e un minimo N 9;4 [] un massimo M 6;1 e un minimo N 9;4
[] un massimo M 6;1 e un minimo N 9;4
[] un massimo M 6;1 e un minimo N 9;4
La curva di equazione y 
7) La funzione
y
x 2  2x  1
x 2  2 x  15
In caso affermativo quali ?
[] massimo in x  1
[] né massimi né minimi
possiede punti di massimo e/o di minimo ?
[] minimo in x  1
[] massimo in x  1 e minimo in x  1
8)Si consideri la funzione y   x 2  3x nell’intervallo 1; 5  ; nei punti  3 ; 9  e  5 ; 5  :
 2
2 4 2 4
[] la funzione assume valori negativi
[] non è presente né il min. né il max. assoluto
[] la funzione assume rispettivamente il max. e il min. assoluto
[] la funzione assume rispettivamente il min. e il max. assoluto
9)A quali coordinate corrisponde il minimo relativo della funzione f ( x) 
[]
[]
[]
[]
(2;8)
(-2;8)
(2;-8)
(-2;-8)
25
x 2  2x  4
:
x
CONCAVITA’
La funzione è concava verso l’alto in xo se il suo grafico in un intorno di xo si trova al di
sopra della retta tangente in P.
La funzione è concava verso il basso se il suo grafico in un intorno xo si trova al di sotto
Della retta tangente in P.
TEOREMA
Consideriamo una funzione che ammette derivata prima e seconda in un punto xo
Se si ha f ‘’(xo)>0 la funzione è concava verso l’alto di xo
Se si ha f ‘’(xo)<0 la funzione è concava verso il basso di xo
ESEMPIO
Determinare gli intervalli in cui la funzione y= 4x3-2x2+6 volge la concavità verso il basso o verso
l’alto.
1) si calcola la derivata prima y’
y’= 12 x2-4x
2) si calcola la derivata seconda y’’
y’’ = 24x-4
3) si pone y’’>0 (per concavità verso alto)
24x-4>0
x>1/6
quindi per x> 1/6 concavità verso alto
4) per y’’<0 x<1/6 concavità verso basso
TEST
1)La concavità di una funzione derivabile si determina:
□ studiando il segno della derivata prima
□ annullando la derivata prima
□ studiando il segno della derivata seconda
□ annullando la derivata seconda
26
PUNTO DI FLESSO
Flessi a tangente orizzontale
Consideriamo una funzione come quella sotto rappresentata, come si può vedere è una funzione
sempre decrescente, essa non ha massimo o minimo relativi, ma ha un flesso in x0.In questo punto
la tangente alla curva taglia la curva ed è parallela all’asse delle ascisse : la sua pendenza è nulla e
quindi si ha f ‘(x0)=0.
Il flesso di questa figura si dice discendente perché la concavità è rivolta prima verso l’alto e poi
verso il basso.
Un flesso si dice invece ascendente quando la concavità è rivolta prima verso il basso e poi verso
l’alto.
Un punto x0 in cui risulta f’(x0) =0 può essere di massimo o minimo relativo ed anche di flesso a
tangente orizzontale. Tali punti in cui si ha f’(x0) =0 vengono detti punti stazionari.
I punti di flesso sono quelli in cui la funzione cambia il verso della concavità.
Teorema I:
Se una funzione f(x) ammette derivata prima e seconda (finite) in un punto xo interno ad un
intervallo (a,b) ed è f’’(xo)≠0, il diagramma della funzione volge, nel punto xo, la concavità
Verso l’alto o verso il basso a seconda che è f’’(x) >0 oppure f’’(x) <0.
In xo si ha un punto di flesso se per x<xo si ha f’’(xo)>0
mentre per x>xo si ha f’’(x) <0
in questo caso la funzione è concava verso l’alto a sinistra di xo concava verso il basso a destra.
(oppure se per x<xo si ha f’’(x) <0 mentre x>xo f’’(x) >0 si ha sempre un punto di flesso).
27
TEOREMA II
Se una funzione y=f(x) ha un flesso in un punto xo, la derivata seconda in quel punto è uguale
a zero.
TEOREMA III
Se f’’(xo)=0 ed è f’’’(xo)≠0 (supposto che esista) il punto F di ascissa xo è effettivamente un
flesso.
TEOREMA IV
Se nel punto xo si annullano, insieme alla derivata seconda,le derivate successive della f(x) e la
prima derivata non nulla in xo è di ordine dispari, il punto del diagramma, il punto di ascissa
xo è un punto di flesso, mentre se la prima derivata non nulla è di ordine pari, il diagramma
nel punto xo volge la concavità verso l’alto o verso il basso secondo che essa è negativa o
positiva.
ESEMPIO
Determinare i punti di flesso della funzione : y= x3-2x2-4x+12
1) Si calcola la derivata prima y’
y’= 3x2-4x-4
2) Si pone la derivata prima uguale a zero y’=0
3x2-4x-4=0
si risolve x1= -2/3 x2=2
3) Si calcola la derivata seconda y’’
y’’= 6x-4
4) Si sostituisce in y’’ i valori x1 e x2 in y’’
y’’(-2/3)= 6.(-2/3)-4=-8 <0
(si avrà un massimo rel.)
y’’(2)= 6.2-4=8 >0
(si avrà un minimo relativo)
Se fosse stato y’’(xo)=0 si prendono in considerazione le derivate successive alla seconda (cioè
4°grado). Se la prima derivata successiva alla seconda diversa da zero è di ordine pari ,si ha
un minimo se è positiva mentre si ha un massimo se è negativa.
Se la prima derivata successiva alla seconda diversa da zero è di ordine dispari si ha un flesso
a tangente orizzontale.
5)si pone y’’=0
6x-4=0 x= 2/3
5) si calcola la derivata terza y’’’
y’’’= 6 che non dipende da x ed è sempre positiva, vuol dire che per x=2/3 la funzione ha un
flesso.
6)si calcola ordinata punto di flesso
sostituendo x=2/3 in
y= x3-2x2-4x+12
y(2/3)= 236/27
F( 2/3, 236/27)
Flessi a tangente obliqua
28
E’ un flesso a tangente obliqua quello evidenziato nella figura sotto, si ha quindi f “ (x0)=0
mentre f’(x0)≠0
Esempio 1.
Determinare gli eventuali flessi della funzione seguente:
3
2
y   x  2   x  1  1
4
1) la derivata prima è :
3
3
9
2
y '  [2 x  2   x  1   x  2 ]   x  2 2 x  2  x  2   x x  2 
4
4
4
2) Per trovare massimi ,minimi e flessi si risolve l’equazione y’=0
9
x  x  2  0
4
Si trovano le soluzioni
x=0 e x=2
3)La derivata seconda è:
9
2 x  2  9 x  1
4
2
4) Si sostituiscono le soluzioni
y '' 
y '' (0) 
9
0  1   9  0
2
2
9
2  1  9  0
2
2
5) si risolve l’equazione y’’=0
x=0
e x=2 al posto di x in y’’
per x=0 si ha un massimo
di ordinata y(0)=4
y '' (2) 
per x=2 si ha un minimo
di ordinata y(2)=1
9
x  1  0
2
e la soluzione è x=1
Si sostituisce nella y’ il valore x=1 se y’ sarà uguale a 0 ci sarà un asintoto orizzontale
29
9
9
y ' (1)  11  2    0
4
4
Siccome risulta y’≠0 non esistono flessi orizzontali.
5)la derivata terza è :
y ''' 
9
0
2
La prima derivata non nulla è di ordine dispari quindi si possono determinare i flessi obliqui e i
versi della concavità di y(x)
6) risolvendo l’equazione y’’=0
9
x  1  0
cioè 2
si era trovato x=1
Nel punto di ascissa x=1 la curva ha un flesso obliquo, che è discendente perché
y’(1) = -9/4 <0
7) calcolo ordinata del punto di flesso
3
x  22 x  1  1 y (1)  3 1  22 1  1  1  5
4
4
2 il flesso è F(1;5/2).
8)L’equazione della tangente in F si trova determinando il coefficiente angolare in questo punto,
cioè il valore della derivata prima in quel punto.
y
9
9
m  y ' (1)  11  2  
4
4
L’equazione della retta tangente è pertanto:
y-yF = m (x-xF)
y
5 9

( x  1)
2 4
quindi :
9x+4y-19=0
Esempio 2
Determinare gli eventuali flessi della funzione seguente:
y  x 5  3x  5
1) la derivata prima è :
y '  5x 4  3
3) La derivata seconda è:
y' '  20 x 3
4) Si risolve y’’=0
20x3=0
x=0
5) Siccome y’(0)=5.0-3=2≠0 non ci sarà flesso orizzontale
6) y’’>0 per x>0 concavità verso alto
y’’<0 per x<0 concavità verso basso
30
7) La derivata terza è:
y ' ' '  60 x 2
8) La derivata quarta è:
y IV  120 x
9) La derivata quinta è:
y V  120  0
la funzione ha un flesso F di ascissa 0
10) Si calcola l’ordinata del punto di flesso
y  x 5  3x  5  05  30  5  5
F(0,5)
11) Si determina l’equazione della tangente di flesso
essendo
y ' (0)  50 4  3  3
Il coefficiente angolare è quindi m=-3
L’equazione della retta tangente è pertanto:
y-yF = m (x-xF)
y-5=-3(x-0)
y-5=-3x
eq. Retta tg : y=-3x+5
Flessi a tangente verticale
E’ un flesso a tangente verticale quello evidenziato nella figura sotto, la retta tangent alla curva
in x0 è perpendicolare all’asse delle ascisse.
Per determinare gli eventuali punti di flesso a tangente verticale bisogna esaminare gli eventuali
punti di infinito della derivata prima.
In x0 esiste un punto di flesso a tangente verticale se risulta :
lim x x0 – f’ ( x) = lim x x0 + f’ ( x)= + 
oppure:
lim x x0 – f’ ( x) = lim x x0 + f’ ( x)= - 
flesso a tangente verticale crescente
flesso a tangente verticale decrescente
31
Esempio :
sia data la funzione y  3 x  2
definita in R
la derivata prima prima è
1
y' 
33 x 2
la funzione non ammette derivata in x=0 mentre esistono sia il
limite destro che il limite sinistro di y’ per x tendente a 0 e tali limiti sono entrambi uguali a +∞.
In questo caso, il flesso a tangente verticale è crescente.
Cuspidi:
lim x x0 + f’ ( x)= - 
oppure:
lim x x0 – f’ ( x) =- 
e lim x x0 – f’ ( x) =+ cuspide con vertice in alto
e lim x x0 + f’ ( x)= + cuspide con vertice verso basso
Esempio 1:
si abbia la funzione :
y  3 x2  4
C.E. =R
1)
Calcolo la derivata prima:
2
y'  3
3 x
32
2) La funzione non è derivabile in x=0 mentre sistono sia il limite sinistro che il limite destro di
y’
2
2
lim x0 3  
lim x0 3  
3 x
3 x
Pertanto per x=0 si ha una cuspide rivolta verso il basso.
Esempio 2:
si abbia la funzione :
y  3 x 2  2
C.E. =R
1)
Calcolo la derivata prima:
2
y'   3
3 x
2) La funzione non è derivabile in x=0 mentre sistono sia il limite sinistro che il limite destro di
y’
2
2
lim x0 3  
lim x0 3  
3 x
3 x
Pertanto per x=0 si ha una cuspide rivolta verso l’alto
TEST
1)Per l’esistenza di un punto di flesso (non a tangente verticale) in x 0 ,la condizione f ' ' ( x0 )  0 è:
[] necessaria e sufficiente
[] sufficiente ma non necessaria
[] non necessaria
[] necessaria ma non sufficiente
2)La funzione y  x 3  3x 2  1 ha:
□ un flesso x  1 , un minimo assoluto in x  2 , un massimo assoluto in x  0
□ un flesso x  1 , un minimo relativo in x  2 , un massimo relativo in x  0
□ non ha punti di minimo e di massimo
□ non ha punti di flesso
MASSIMI E MINIMI ASSOLUTI
Per calcolare il massimo o il minimo assoluto di una funzione definita in un intervallo (a,b) si
calcolano le ascisse dei suoi punti estremanti, si confrontano quindi i valori che la funzione
acquista in tali punti e agli estremi dell’intervallo di definizione; il più grande di tali valori è il
massimo assoluto; il più piccolo è il minimo assoluto.
33
ESEMPIO
Trovare massimi e minimi assoluti della funzione y= x3-3x nell’intervallo (-2,3)
1) Si calcola la derivate prima y’= 3x2-3
2) Si pone la derivata prima uguale zero
y’=0
3x2-3=0
e si trovano le soluzioni
3) Si calcola la derivata seconda
x=-1 x=+1
y’’=6x
4) Si sostituiscono in y’’ le due soluzioni x=-1 e x=1
y’’(1)=6 >0 essendo >0
in x=1 minimo relativo
y’’(-1)= -6 <0 essendo <0
in x=-1 massimo relativo
5) Trovo le ordinate dei massimi e dei minimi relativi sostituendo
nella y= x3-3x i valori x=1 e x=1 quindi in (1,-2) minimo relativo e in (-1,2) massimo
relativo
6) Trovo le ordinate dei valori dell’intervallo (-2,3) sostituendo nella y= x3-3x i valori
x=-2 e x=3 e ricavo:
y(-2)=-2
y(3)=18
7) confronto questi valori con quelli dei massimi e minimi relativi
y(-2)=-2
y(-1)=2
y(1)=-2
y(3)=18
in x=-2 e in x= 1 due minimi assoluti ( i valori minori sono -2)
in x= 3 vi è un massimo assoluto (i valori più alto è 18),quindi :
punti di minimo assoluto m1 (-2;-2) m2(1;-2)
punto di massimo assoluto M (3,18).
TEST
1) La funzione y  x 3  3x 2  1 ha:
□ un flesso x  1 , un minimo assoluto in x  2 , un massimo assoluto in x  0
□ un flesso x  1 , un minimo relativo in x  2 , un massimo relativo in x  0
□ non ha punti di minimo e di massimo
□ non ha punti di flesso
2) Data la funzione y  2 x 3  15 x 2  24 x stabilire se nell’intervallo (1,5):
34
□
□
□
□
ammette massimo e minimo assoluti
ammette massimo assoluto ma non il minimo assoluto
ammette minimo assoluto ma non il massimo assoluto
non ammette né massimo né minimo assoluti
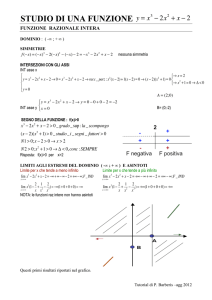
LO STUDIO DI UNA FUNZIONE
1) INDIVIDUAZIONE DEL DOMINIO DELLA FUNZIONE
2) RICERCA DI EVENTUALI SIMMETRIE
Se f(-x) = f(x) la funzione è pari e il suo grafico è simmetrico rispetto all’asse delle ordinate.
si può quindi studiare la funzione solo per valori di x positivi o nulli.
Se f(-x)=- f(x) la funzione è dispari e il suo grafico è simmetrico rispetto origine degli assi.
3) RICERCA DI EVENTUALI PERIODICITA’ DELLE FUNZIONI
( funzioni goniometriche)
4) COMPORTAMENTO DELLA FUNZIONE AGLI ESTREMI DEL DOMINIO E
RICERCA EVENTUALI ASINTOTI.
5) STUDIO DEL SEGNO DELLA FUNZIONE
( y>0 e y<0)
6) CALCOLO y’ per:
 individuare gli intervalli in cui la funzione è crescente o decrescente (y’>0 , y’<0)
 calcolo eventuali punti di massimo e minimo relativi
7) CALCOLO y’’ per:
 individuare la concavità della curva (y’’>0 o y’’<0)
 individuare eventuali punti di flesso
35