servizi online

ESERCITAZIONE SF 25/11/2014
Capitolo 1 – Gli strumenti dell’analisi normativa – Riepilogo teoria

Economia di puro scambio
Consideriamo un’economia di puro scambio con due soli individui, A e B, e due soli beni, il bene X e il bene
Y. A e B posseggono determinate dotazioni iniziali dei beni X e Y. Le dotazioni iniziali non soddisfano
necessariamente i bisogni degli agenti, cioè il paniere di consumo iniziale di A e B non è necessariamente
ottimale.
Inoltre gli agenti non sono in grado di produrre ulteriori unità di X e Y e possono soltanto decidere
autonomamente se consumare semplicemente tali dotazioni oppure se modificare l’allocazione iniziale
scambiando tra di loro parte delle dotazioni.
Possiamo descrivere lo scambio in termini analitici. Indichiamo con 𝑥̅ , 𝑦̅ le dotazioni iniziali totali dei beni X e
Y. Indichiamo le rispettive dotazioni individuali di A e B con (𝑥̅𝐴 , 𝑦̅𝐴 ) e (𝑥̅𝐵 , 𝑦̅𝐵 ). Le generiche allocazioni
alternative sono indicate invece con (𝑥𝐴 , 𝑦𝐴 ) e (𝑥𝐵 , 𝑦𝐵 ).
Le allocazioni effettivamente raggiungibili devono rispettare il vincolo dato dalle risorse originarie:
𝑥𝐴 + 𝑥𝐵 = 𝑥̅ ∪ 𝑦𝐴 + 𝑦𝐵 = 𝑦̅.
Ora utilizziamo l’espediente ideato da Edgeworth per ottenere una rappresentazione grafica congiunta delle
preferenze dei due individui. Indichiamo in un diagramma cartesiano la dotazione iniziale di A e sullo stesso
diagramma rappresentiamo la dotazione iniziale di B invertendo i riferimenti agli assi cartesiani.
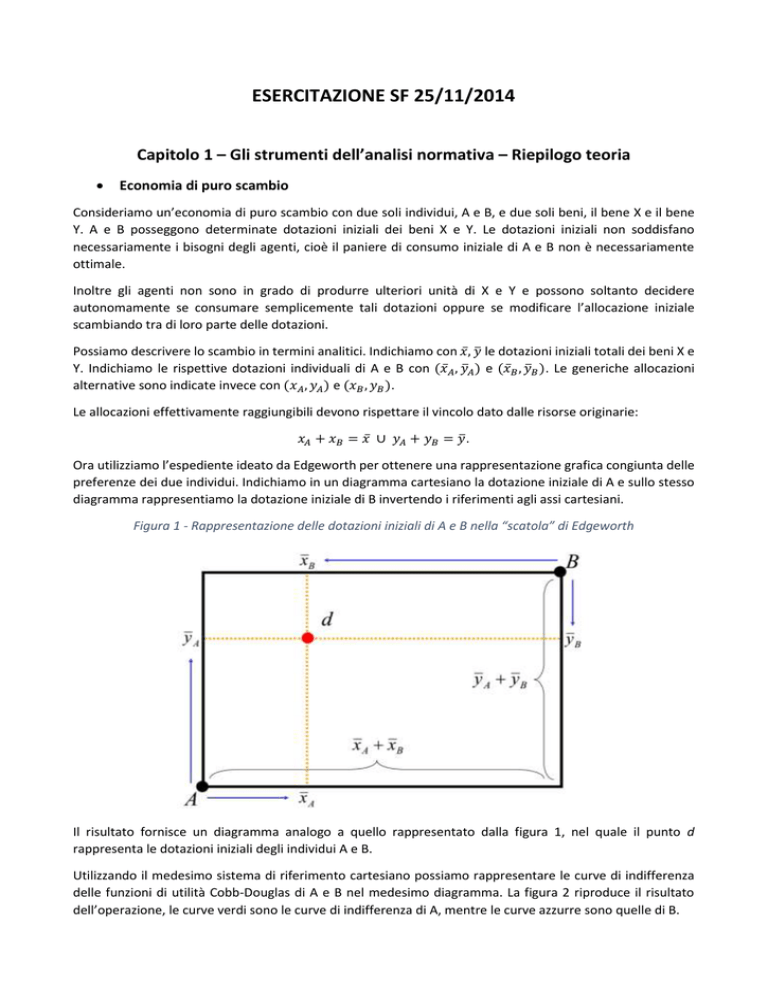
Figura 1 - Rappresentazione delle dotazioni iniziali di A e B nella “scatola” di Edgeworth
Il risultato fornisce un diagramma analogo a quello rappresentato dalla figura 1, nel quale il punto d
rappresenta le dotazioni iniziali degli individui A e B.
Utilizzando il medesimo sistema di riferimento cartesiano possiamo rappresentare le curve di indifferenza
delle funzioni di utilità Cobb-Douglas di A e B nel medesimo diagramma. La figura 2 riproduce il risultato
dell’operazione, le curve verdi sono le curve di indifferenza di A, mentre le curve azzurre sono quelle di B.
Figura 2 - Rappresentazione delle curve di indifferenza di A e B nella “scatola” di Edgeworth
La lunghezza dell’asse orizzontale della scatola di Edgeworth in figura 2 è pari alla somma della distanza
orizzontale tra l’origine e il punto della dotazione iniziale di bene X di A e la distanza orizzontale tra l’origine
e il punto che indica la dotazione iniziale di bene X di B. In altri termini, la lunghezza dell’asse orizzontale è
pari esattamente alla dotazione complessiva del bene X disponibile ai due individui. Discorso analogo vale
per l’altezza della scatola di Edgeworth, con riferimento al bene Y.
Si noti dalla figura 3 che, per l’individuo A, tutte le allocazioni evidenziate al di sopra della curva verde sono
preferite rispetto al punto della dotazione iniziale d.
Figura 3 - Curva di indifferenza di A nella “scatola” di Edgeworth
Per l’individuo B invece, tutte le allocazioni al di sotto della curva azzurra sono preferite al punto della
dotazione iniziale d (figura 4).
Figura 4 - Curva di indifferenza di B nella “scatola” di Edgeworth
Allocazioni alternative poste all’interno dell’are delimitata dalle curve di indifferenza delle figure 3 e 4
rappresentano dei miglioramenti Paretiani, ossia aumentano l’utilità di entrambi gli individui. Un
allocazione Pareto efficiente invece sì ha quando non è più possibile aumentare l’utilità di un individuo
senza diminuire quella dell’altro. Tale allocazione è descritta dal punto e nella figura 5
Figura 5 – Allocazione Pareto efficiente
Se l’allocazione Pareto efficiente si trova strettamente all’interno della scatola di Edgeworth, la Pareto
efficienza richiede che le curve di indifferenza siano tangenti, quindi le allocazioni interne Pareto efficienti
sono caratterizzate dal fatto che i saggi marginali di sostituzione dei consumatori sono uguali:
𝐴
𝑆𝑀𝑆𝑥𝑦
=
𝐵
𝑆𝑀𝑆𝑥𝑦
,
con
𝑖
𝑆𝑀𝑆𝑥𝑦
=
𝜕𝑈𝑖
𝜕𝑥
𝜕𝑈𝑖
𝜕𝑦
.
Se le funzioni di utilità sono regolari (convesse, beni perfetti sostituti o perfetti complementi), la condizione
di uguaglianza dei due saggi marginali di sostituzione permette di definire, all’interno della scatola di
Edgeworth, il luogo geometrico delle allocazioni Pareto efficienti, comunemente noto con l’appellativo di
“curva dei contratti” (figura 6).
Figura 6 – Curva dei contratti.

Frontiera delle possibilità produttive o curva di trasformazione
Il trade-off tra la produzione dei diversi beni è alla base dell'inclinazione negativa della curva di
trasformazione (figura 7). Ad esempio, in un sistema economico ipotetico le risorse possono essere utilizzate
per produrre solo 10 unità di bene X, solo 10 unità di bene Y o diverse combinazioni (𝑥, 𝑦) dei due beni. Il
𝐶′
saggio marginale di trasformazione SMT indica la pendenza della curva (o alternativamente 𝑆𝑀𝑇𝑥𝑦 = 𝐶𝑥′ ).
𝑦
Figura 7 – Curva di trasformazione.

Primo teorema fondamentale dell’economia del benessere
Massimizzazione utilità individuo A:
𝑃
𝐴
𝑆𝑀𝑆𝑥𝑦
= 𝑃𝑥 .
𝑦
Massimizzazione utilità individuo B:
𝑃
𝐵
𝑆𝑀𝑆𝑥𝑦
= 𝑃𝑥 .
𝑦
Ne deriva la condizione di Pareto efficienza vista in precedenza.
𝐴
𝐵
𝑆𝑀𝑆𝑥𝑦
= 𝑆𝑀𝑆𝑥𝑦
.
Inoltre in un mercato concorrenziale si ha che:
𝐶𝑥′ 𝑃𝑥
=
𝐶𝑦′ 𝑃𝑦
Ossia che
𝑆𝑀𝑇𝑥𝑦 =
𝑃𝑥
𝑃𝑦
Se c’è perfetta concorrenza e tutti gli individui massimizzano la propria utilità (o profitto) allora si riproduce
il risultato di allocazione Pareto efficiente
𝑃
𝐴
𝐵
𝑆𝑀𝑆𝑥𝑦
= 𝑆𝑀𝑆𝑥𝑦
= 𝑆𝑀𝑇𝑥𝑦 = 𝑃𝑥 .
𝑦

Secondo teorema fondamentale dell’economia del benessere
Un’allocazione Pareto efficiente può non essere ritenuta la migliore dalla collettività. La collettività può
preferire una distribuzione più equa. L'efficienza paretiana non “ordina” le preferenze e non è compatibile
con giudizi di valore.
La curva dei contratti stabilisce implicitamente una relazione tra la massima utilità di un consumatore rispetto
all’altro consumatore. Se riportiamo su un riferimento cartesiano le combinazioni di UA e UB individuate
lungo la curva dei contratti, otteniamo una curva come quella riportata nel grafico successivo, che prende il
nome di curva o frontiera delle utilità possibili. Le combinazioni individuata lungo la frontiera o al di sotto di
questa sono raggiungibili per la collettività; tutti quelli al di sopra non lo sono.
Figura 8 – frontiera delle utilità possibili
Tutti i punti sulla frontiera delle possibili utilità rappresentano distribuzioni diverse delle risorse. Si può
dimostrare che redistribuendo i redditi iniziali dei due consumatori è possibile raggiungere un qualsiasi punto
della frontiera delle utilità possibili.
Qual è l’allocazione migliore secondo la società? Per rispondere a questa domanda si postula l’esistenza di
una funzione di benessere sociale. Si tratta di una rappresentazione delle preferenze della società basata
sulla distribuzione delle utilità tra i suoi membri, ossia 𝑊 = 𝑓(𝑈1 , 𝑈2 , … , 𝑈𝑛 ), crescente al crescere degli
individui. Dalla funzione di benessere sociale si ricava una mappa di curve di indifferenza sociale che
rappresentano le alternative allocazioni di utilità individuali.
La collettività può preferire una distribuzione più equa anche se non efficiente. Il punto a nelle figura 9
massimizza il benessere sociale dato il vincolo della frontiera delle utilità possibili.
Figura 9 – Massimizzazione del benessere sociale

Fallimenti del mercato
Le condizioni di validità del primo teorema fondamentale dell’economia del benessere sono:
-
Gli agenti operano come price-takers;
Completezza dei mercati e assenza di esternalità;
Assenza di beni pubblici;
Assenza di asimmetrie informative.
Il primo teorema del benessere dice che se sono soddisfatte le precedenti condizioni allora
l'equilibrio è efficiente, cioè non si può fare di meglio nel senso di Pareto.
Nel caso in cui in un'economia di mercato venga violato uno di questi principi (fallimento del mercato),
secondo Pareto è da ritenersi giustificato l'intervento pubblico.
Una prima fonte di fallimenti del mercato sarebbe legata alla presenza di costi e/o benefici esterni al mercato
stesso. Esempi sono dati da:
-
Assenza di concorrenza (Monopolio, oligopolio, monopsonio ecc.)
Esternalità (mancate compensazioni di prezzo)
Beni pubblici (Beni non rivali e inoltre non si può escludere un individuo dal consumo)
Mancanza di definizione di diritti di proprietà
Asimmetrie informative (Selezione avversa, azzardo morale, problemi principale-agente)
Gli strumenti dell’analisi normativa – Esercizi
Esercizio 3.1
a. In questo particolare mercato assicurativo, non ci si aspetterebbe che l’asimmetria informativa sia
un grosso problema, in quanto la probabilità che si verifichi un’inondazione è nota a tutti. L’azzardo
morale potrebbe essere un problema: la gente costruirà con maggiore probabilità nei pressi di una
spiaggia se possiede un’assicurazione contro le inondazioni. Ciononostante, ci si aspetterebbe che il
mercato delle assicurazioni contro le inondazioni funzioni in modo piuttosto efficiente.
b. Esiste una notevole asimmetria informativa nei mercati delle assicurazioni medico- sanitarie per i
consumatori e anche delle assicurazioni contro gli errori dei medici. Perché si realizzi un livello
efficiente di consumo, il prezzo deve essere pari al costo marginale e l’effetto dell’assicurazione
potrebbe essere quello di abbassare la percezione del prezzo relativo al consumo di cure sanitarie, il
che comporterebbe un consumo superiore al livello efficiente. A causa della regolamentazione, delle
assicurazioni, delle imposte e del trasferimento dei costi dal non assicurato all’assicurato, vi sono
pochi motivi per credere che il mercato sia efficiente.
c. Nel mercato azionario, vi è un buon livello di informazione e migliaia di acquirenti e venditori. In linea
di massima, ci si aspetta degli esiti efficienti.
d. Da un punto di vista nazionale, esiste molta competizione e informazione nel campo dei personal
computer. L’esito sarà probabilmente efficiente per le componenti hardware. Tuttavia, alcune
aziende potrebbero esercitare un certo potere di mercato, in particolar modo nel mercato dei
software; in questi mercati potrebbero essere presenti delle “esternalità di rete”, nella misura in cui
il valore di un linguaggio di programmazione o di un software dipende dal numero di altri utenti che
lo utilizzano.
e. L’allocazione nel mercato privato sarà probabilmente inefficiente senza l’intervento da parte dello
Stato. Il mercato dei prestiti universitari potrebbe essere soggetto ad asimmetria informativa: lo
studente sa meglio dell’ente che eroga il prestito se lo estinguerà o meno; è una forma di selezione
avversa. In questo caso, l’intervento da parte dello Stato non “risolve” il problema della selezione
avversa (dal momento che la partecipazione al programma di prestito agli studenti non è
obbligatoria), ma può creare un mercato che non esisterebbe in assenza di tale intervento.
f.
Vi sono molte ragioni per ritenere che la fornitura di assicurazioni automobilistiche sia con molta
probabilità inefficiente in mancanza di intervento da parte dello Stato. Al pari degli altri mercati
assicurativi, quello delle assicurazioni automobilistiche è soggetto ad asimmetria informativa. I
conducenti che sanno di essere fortemente inclini a fare incidenti saranno particolarmente
interessati a stipulare delle assicurazioni automobilistiche (o delle polizze che offrano loro una
copertura anche maggiore), mentre quelli che sono meno inclini a fare incidenti (o sono in grado di
auto-assicurarsi) potrebbero scegliere di non stipulare affatto un’assicurazione. Obbligando gli
individui a stipulare un’assicurazione automobilistica qualora essi scelgano di guidare, il problema
della selezione avversa risulta per certi versi alleviato (ma anche in questo caso i conducenti più inclini
a fare incidenti potrebbero assicurarsi maggiormente). Un’altra imperfezione di mercato, collegata
alla “sottoassicurazione” ha a che fare con le esternalità finanziarie connesse a un incidente
automobilistico: un automobilista “sottoassicurato” colpevole di aver causato l’incidente potrebbe
non avere un reddito sufficiente per coprire i danni arrecati all’altro conducente, e rivelarsi
inadempiente dichiarando il fallimento. Questo stratagemma crea vari problemi di azzardo morale.
Esercizio 3.2
Il punto a rappresenta un’allocazione equa dell’acqua, ma non efficiente, in quanto le curve non sono
tangenti. Il punto b è una delle molte allocazioni Pareto efficienti e rappresenta un caso in cui Caterina trae
un enorme beneficio dallo scambio, mentre l’utilità di Enrico rimane invariata rispetto all’assegnazione
iniziale.
Esercizio 3.3
Il saggio marginale di trasformazione fra film stranieri e nazionali dipende dai rapporti fra i loro prezzi al
lordo di imposte e sussidi. A causa del dislivello creato da imposte e sussidi, i due rapporti di prezzo sono
diversi. Pertanto, saggio marginale di sostituzione e saggio marginale di trasformazione non sono uguali, e
l’allocazione delle risorse non è efficiente.
Esercizio 3.4
Un bene meritorio (o di merito) è un bene che gode di particolare tutela pubblica indipendentemente dalla
richiesta che ne fanno i potenziali utenti. Il concetto è stato introdotto, nella letteratura economica, da R.
Musgrave nel 1959. Un bene di merito è rivolto al soddisfacimento di bisogni importanti per la collettività
(per es. l’istruzione, il servizio sanitario, i consumi necessari al minimo vitale, la sicurezza per gli automobilisti
fornita dalle apposite cinture ecc.) e nei riguardi del quale il bilancio pubblico ha il compito di garantire una
produzione ottimale, rispetto a quella che si determinerebbe laddove il suo livello fosse rimesso alla sola
dinamica del mercato (produzione subottimale).
La natura del b. m. è stata spesso confusa con quella del b. pubblico. Pur condividendo con i beni pubblici la
caratteristica di produrre effetti esterni sulla collettività, i beni meritori si distinguono per gli aspetti della
rivalità nel consumo e dell’escludibilità dal beneficio, tipici dei beni privati.
Pertanto l’organizzazione di concerti gratuiti da parte del comune di Roma è giustificabile qualora la dinamica
del mercato della musica dal vivo producesse un output subottimale e qualora il contenuto del concerto sia
ritenuto rivolto ad un soddisfacimento di un bisogno importante della collettività.
Esercizio 3.5
In questo caso, la scatola di Edgeworth di fatto è una retta in quanto sull’isola c’è soltanto un bene. La serie
delle possibili allocazioni è una linea retta, lunga 100 unità. Ogni allocazione è Pareto efficiente, dal momento
che l’unico modo per migliorare le condizioni di un individuo consiste nel peggiorare quelle dell’altro. Nel
libro non viene presentata alcuna teoria che possa essere di aiuto nel decidere se un’allocazione è equa. Per
quanto il fatto di suddividere le noccioline in parti uguali fra gli individui possa essere equo, potrebbe non
esserlo nel momento in cui le “necessità” caloriche dei vari individui sono diverse. Con una funzione del
benessere sociale è possibile valutare se la ridistribuzione in tutta la società intesa sia una cosa positiva.
Esercizio 3.6
Sulla base di questo criterio, sembrerebbe che i mercati costituiscano un ordine sociale positivo. Ciascuno
agisce in modo egoistico (ossia massimizza la propria utilità), ma ne risulta un’allocazione delle risorse Pareto
efficiente. Il presupposto, ovviamente, è che siano valide tutte le condizioni del primo teorema
fondamentale.
Esercizio 3.7
Sebbene il saggio marginale di sostituzione di Vittoria sia pari a quello di Alberto, non è pari al saggio
marginale di trasformazione, per cui l’allocazione non è Pareto efficiente. Entrambi cederebbero due tazze
di tè in cambio di una scatola di biscotti ma, secondo la funzione di produzione, potrebbero di fatto ottenere
sei scatole di biscotti rinunciando a due tazze di tè. Cedendo le tazze di tè in cambio delle scatole di biscotti
entro la funzione di produzione, le utilità di entrambi risultano incrementate.
Esercizio 3.8
a. Falsa. Come illustrato nel testo, l’uguaglianza fra i tassi marginali di sostituzione è una condizione
necessaria, ma non sufficiente. Anche il saggio marginale di sostituzione (MRS) di ciascun individuo
deve essere pari al saggio marginale di trasformazione (MRT).
b. Incerta. Nella misura in cui l’allocazione è una soluzione interna nella scatola di Edgeworth, i saggi
marginali di sostituzione degli individui devono essere uguali. Non necessariamente ciò deve essere
vero, tuttavia, negli angoli in cui un consumatore possiede tutti i beni dell’economia.
c. Vera.
d. Falsa.
Capitolo 3 – Beni pubblici – Riepilogo teoria
Per i beni privati, rivali ed escludibili, la curva di domanda di mercato è ottenuta attraverso la somma in
orizzontale delle curve di domanda individuali (figura 10).
Figura 10 – Domanda di mercato dei beni privati
La condizione di efficienza dell’offerta dei beni privati, secondo Samuelson, risulta essere pertanto:
𝑆𝑀𝑆 𝑎 = 𝑆𝑀𝑆 𝑏 = 𝑆𝑀𝑇.
Si noti che nella figura 10 ci si riferisce ad un singolo bene X. In realtà è implicita la presenza di un secondo
bene Y il cui prezzo è stato posto uguale all’unità (bene numerario). Ne deriva che la condizione di
𝑖
massimizzazione dell’utilità del singolo consumatore è 𝑆𝑀𝑆 𝑖 = 𝑆𝑀𝑆𝑥𝑦
= 𝑃𝑥 . In altre parole 𝑆𝑀𝑆 𝑖 può essere
interpretato come la disponibilità a pagare il bene X da parte del consumatore i-esimo.
I beni pubblici, a differenza dei beni privati sono non rivali e non escludibili.
Un bene è non rivale quando il consumo di ciascun individuo non comporta alcuna sottrazione nel consumo
dello stesso bene da parte di un altro individuo. In altre parole il costo marginale di un consumatore
aggiuntivo è uguale a 0. Esempi di beni non rivali possono essere la difesa nazionale, l’illuminazione pubblica
ecc.
L offerta ’offerta di un bene non rivale è disponibile modo congiunto per tutti gli individui. Il vincolo di scarsità
citato in precedenza per i beni privati (rivali) era dato da: 𝑥𝐴 + 𝑥𝐵 = 𝑥̅ . Per i beni pubblici, non rivali, esso è
dato da: 𝑥𝐴 = 𝑥𝐵 = 𝑥̅ .
Un bene è non escludibile quando non è possibile escludere un soggetto dal consumo del bene (a meno di
costi elevatissimi). In una logica di mercato dovrebbero essere esclusi gli individui che non sono disponibili a
pagare il prezzo. Esempi di beni non rivali possono essere la difesa nazionale, un parco nazionale ecc.
La non escludibilità di un bene è collegata all’indivisibilità dei benefici derivanti da quel bene: tutti consumano
la stessa quantità del bene e non è possibile determinare in che misura ciascun individuo beneficia dello
stesso.
La non escludibilità è causa il problema del free riding: gli individui non hanno interesse a rivelare le proprie
preferenze (le proprie valutazioni marginali sul bene) perché a prescindere dalla loro contribuzione potranno
comunque godere del bene da cui non possono essere esclusi.
La figura 11 schematizza le caratteristiche peculiari delle diverse tipologie di beni, classificati in base al grado
di rivalità ed escludibilità.
Figura 11 – Beni privati, pubblici e misti
L’esistenza di beni pubblici fa sorgere due questioni fondamentali relative all’efficienza della loro
produzione:
1. L’esistenza di beni pubblici modifica la condizione di efficienza paretiana?
2. In presenza di beni pubblici il mercato è in grado di realizzare questa condizione di efficienza?
Esistono ancora i presupposti per la validità del primo teorema dell’economia del benessere?
Come si è visto in precedenza la condizione di efficienza in mercato caratterizzato da beni privati era:
𝐴
𝐵
𝑆𝑀𝑆𝑥𝑦
= 𝑆𝑀𝑆𝑥𝑦
= 𝑆𝑀𝑇𝑥𝑦 .
È possibile estendere il primo teorema dell’economia del benessere ai beni pubblici e definire il livello
ottimale di offerta e produzione di beni pubblici? Il problema è stato risolto nel mondo del first best da
P.A.Samuelson (1954). La Samuelson rule risolve il problema della rivelazione delle preferenze, assumendo
che la decisione sulla quantità ottimale sia presa a monte da un arbitro: un dittatore benevolente.
Date le risorse disponibili e data la tecnologia è l’arbitro che perviene all’allocazione efficiente del mix
ottimale tra i beni pubblici e i beni privati attraverso la costruzione della curva residuale. L’idea della curva
residuale consiste nel fissare il livello di utilità di un individuo A sulla curva di indifferenza (elemento di
carattere distributivo) e nel calcolare la curva residuale di beni che restano all’individuo B fissata l’utilità di
A. In seguito si massimizza l’utilità di B data la curva residuale (figura 12).
In corrispondenza del punto E nelle figura 12 si ha la condizione di efficienza del mercato in presenza di beni
pubblici, ossia:
𝐴
𝐵
𝑆𝑀𝑆𝑥𝑦
+ 𝑆𝑀𝑆𝑥𝑦
= 𝑆𝑀𝑇𝑥𝑦 .
In altre parole il saggio marginale di trasformazione di un bene pubblico deve essere uguale alla somma delle
disponibilità a pagare di tutti gli individui.
Ne consegue che la curva di domanda del mercato in presenza di beni pubblici è data dalla somma verticale
delle disponibilità a pagare dei vari individui. Ossia è data dalla disponibilità complessiva a pagare dell’intera
società (figura 13).
Figura 12 – Condizione di efficienza in presenza di beni pubblici
Figura 13 – Domanda beni pubblici
Capitolo 3 – Beni pubblici – Esercizi
Esercizio 4.1
a. Le aree naturali incontaminate sono un bene pubblico impuro: a un certo punto il consumo diventa
non rivale; tuttavia non è escludibile.
b. L’acqua è un bene rivale nel consumo ed escludibile. Pertanto non è un bene pubblico.
c. I corsi universitari di medicina sono un bene privato.
d. I programmi della televisione pubblica sono non rivali nel consumo.
e. Un sito Internet è non rivale nel consumo (sebbene sia escludibile).
Esercizio 4.2
Ipotizziamo che l’utilità di Citah non rientri nella funzione del benessere sociale, per cui l’allocazione
dell’offerta di lavoro nelle varie attività non è rilevante.
a. Il bene pubblico è la sorveglianza; quello privato è la frutta.
b. Si ricordi che, perché vi sia efficienza, è necessario che MRSt + MRSj = MRT. MRSt = MRSj = 2, ma
MRT = 3, per cui MRSt + MRSj > MRT. Per raggiungere un’allocazione efficiente, Citah dovrebbe
intensificare l’attività di raccolta in maniera da ottenere 4 kg per ora.
Esercizio 4.3
Un bene pubblico puro è non rivale nel consumo, per cui è necessario determinare se l’autostrada lo sia o
meno. Ossia, se il costo supplementare connesso al “consumo” dell’autostrada da parte di un’altra persona
è pari a zero, si tratta di un bene pubblico; pertanto, nella misura in cui l’autostrada non è congestionata dal
traffico, può essere considerata un bene pubblico. Tuttavia, l’aggiunta di un ulteriore automobilista a
un’autostrada già di per sé congestionata dal traffico può causare degli ingorghi, i quali si traducono in tempi
maggiori di percorrenza e quindi in costi annessi non pari a zero. Pertanto, è il livello di congestione del
traffico a determinare se possiamo considerare l’autostrada un bene pubblico o meno.
Per determinare se la privatizzazione dell’autostrada rappresenti o meno un’idea ragionevole, è necessario
valutare vantaggi e svantaggi di tale intervento. Innanzitutto, se la struttura del mercato è tale per cui la
privatizzazione dell’autostrada comporterebbe che un monopolista ne assuma il controllo, sarebbe
inefficiente. Inoltre, sarebbe difficile per lo Stato stipulare un contratto completo per la manutenzione
dell’autostrada, il che a sua volta produrrebbe delle inefficienze risultanti dalla privatizzazione. Tuttavia,
qualora fosse lo Stato il proprietario dell’autostrada, potrebbe non avere gli incentivi adeguati per
mantenerla efficiente. In tal caso, anche la proprietà da parte di un monopolista potrebbe rappresentare
un’idea ragionevole.
Esercizio 4.4
La somma dei benefici marginali è pari al costo marginale in corrispondenza di 20 gradi.
Esercizio 4.5
Gli aeromobili sono beni sia rivali sia escludibili, per cui la loro produzione da parte del settore pubblico non
è giustificata sulla base della teoria dei beni pubblici. Se i decisori politici partono dal presupposto che i
benefici del mega jet siano pubblici, troverebbero il livello efficiente di produzione sommando
verticalmente, piuttosto che orizzontalmente, le curve della domanda. Questo fa sì che i benefici risultino di
gran lunga gonfiati e potrebbe essere utilizzato come pretesto per giustificare dei costi così elevati.
Esercizio 4.6
Il beneficio marginale di Thelma è MBT = 12 − Z, mentre quello di Louise è MBL = 8 − 2Z. Il beneficio marginale
complessivo della società è dato dalla somma dei due benefici marginali, ossia MB = 20 − 3Z (per Z ≤ 4), ed è
pari alla curva del beneficio marginale di Thelma successivamente (per Z > 4).
Il costo marginale è costante a MC = 16. Stabilendo MB = MC lungo il primo segmento, si ottiene 20 − 3Z =
16, o Z = 4/3, che è il livello efficiente dei servizi di spazzaneve. Si noti che se Thelma o Louise dovessero
sostenere individualmente l’intero costo, non vi sarebbe alcun servizio di spazzaneve in quanto il costo
marginale di 16 euro supera ciascuno dei loro benefici marginali derivanti dal primo spazzaneve (12 euro o 8
euro). Perciò, si tratta chiaramente di uno dei casi in cui il mercato privato non funziona molto bene. Tuttavia,
si noti inoltre che se il costo marginale fosse leggermente inferiore (per esempio MC ≤ 8), potrebbe essere
che Louise abbia un comportamento opportunistico (problema del free rider).
Esercizio 4.7
Non esiste alcun argomento convincente a sostegno della teoria secondo la quale i musei debbano essere
gestiti dallo Stato sulla base della teoria dei beni pubblici; non è pertanto opportuno pensare alla
privatizzazione. L’ingresso ai musei è chiaramente escludibile; la visione delle opere d’arte è anche un bene
rivale, dal momento che si crea congestione quando troppe persone lo consumano. Perciò i musei
potrebbero essere considerati dei beni privati, piuttosto che pubblici. Per quanto riguarda la diversità di gusti,
con molta probabilità un museo privato deciso a massimizzare i profitti andrà maggiormente incontro ai gusti
dei consumatori rispetto a un museo pubblico (per esempio adottando nuove tecnologie che rendano il
museo più godibile da parte del consumatore tipo). Per quanto riguarda i problemi distributivi invece, è
probabile che il settore privato sia meno sensibile rispetto a quello pubblico.
Esercizio 4.8
a. La curva del beneficio marginale di Zaccaria indica che il beneficio marginale derivante da un faro
comincia in corrispondenza di 90 euro e cala, mentre per Giacomo comincia in corrispondenza di 40
euro e cala. Nessuno dei due attribuisce al primo faro un valore pari al suo costo marginale di 100
euro, per cui nessuno sarebbe disposto da solo a pagare per un faro.
b. Il beneficio marginale di Zaccaria è MBZ = 90 − Q, mentre quello di Giacomo è MBG= 40 − Q. Il
beneficio marginale dell’intera società è pari alla somma dei due benefici marginali, o MB = 130 − 2Q
(per Q ≤ 40), ed è pari alla curva del beneficio marginale di Zaccaria successivamente (per Q > 40). Il
costo marginale è fisso a MC = 100, per cui l’intersezione del beneficio marginale aggregato e del
costo marginale si produce in corrispondenza di una quantità inferiore a 40. Stabilendo MB = MC si
ottiene 130 − 2Q = 100, o Q = 15. Il beneficio netto può essere misurato considerando l’area compresa
fra la curva di domanda e il beneficio marginale della 15a unità. Il beneficio netto è pari a 112,5 euro
per ciascuno, per un totale di 225 euro.
Capitolo 5 – Scelta sociale – Riepilogo teoria
I giudizi di valore alla base di una generica funzione di benessere sociale (FBS) sono i seguenti.
-
Welfarismo: la FBS è funzione di tutte le utilità dei singoli individui.
Indiividualismo: l’utilità degli individui è valutata dai singoli individui stessi.
Principio debole del Pareto: le derivate parziali della FBS rispetto alle singole utilità individuali sono
tutte maggiori o uguali a zero.
Altra proprietà desiderabile è che la riduzione del grado di disuguaglianza non faccia diminuire la FBS. Ossia
le derivate parziali seconde rispetto alle singole utilità sono minori o uguali a zero. Nel caso siano minori di
zero si ha avversione alla diseguaglianza.
FBS notevoli:
-
FBS utilitarista: somma delle utilità individuali. Indifferenza alla diseguaglianza
FBS rawlsiana: uguale al minimo tra le utilità individuali. Massima avversione alla disuguaglianza.
Capitolo 3 – Scelta sociale – Esercizi
Esercizio 3.1
Pareto: tutte quelle sulla frontiera delle utilità.
Utilitarismo: somma delle utilità -> utilità 10 ad A.
Rawls: massimizzare il minimo -> 3.3333