“MODULAZIONE DI FREQUENZA (FM)”
La MODULAZIONE DI FREQUENZA è una tecnica in grado di variare la frequenza della
portante in base alle variazioni della modulante.
Vm(t)
t
Vp(t)
t
fp + f
fp
fp + f
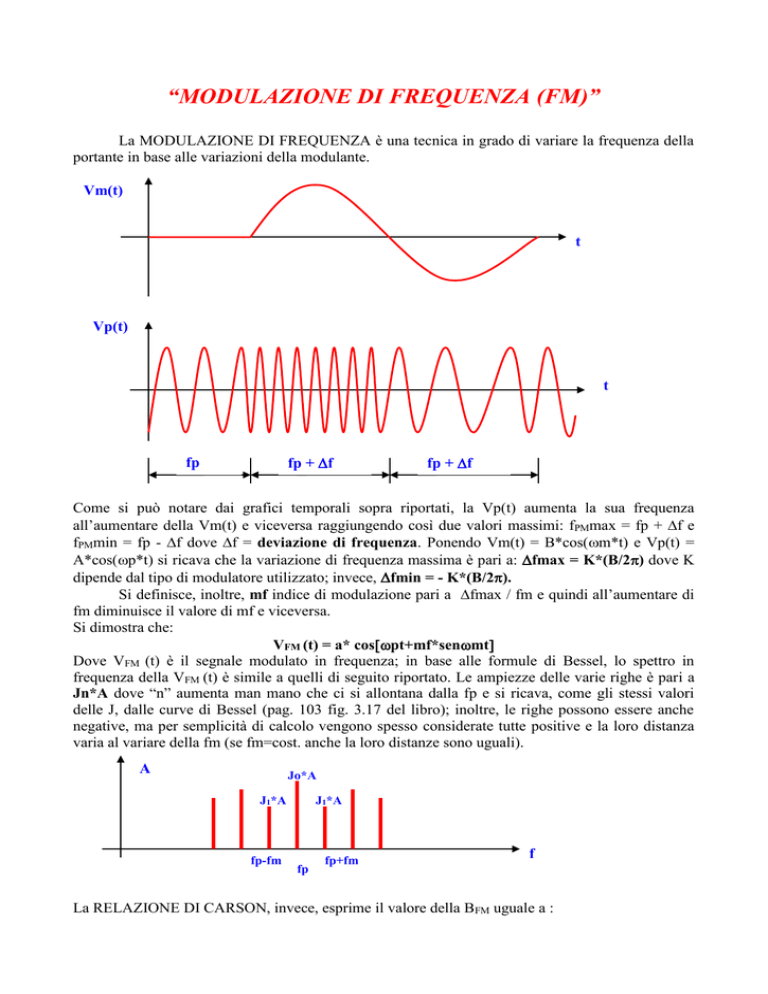
Come si può notare dai grafici temporali sopra riportati, la Vp(t) aumenta la sua frequenza
all’aumentare della Vm(t) e viceversa raggiungendo così due valori massimi: fPMmax = fp + f e
fPMmin = fp - f dove f = deviazione di frequenza. Ponendo Vm(t) = B*cos(m*t) e Vp(t) =
A*cos(p*t) si ricava che la variazione di frequenza massima è pari a: fmax = K*(B/2) dove K
dipende dal tipo di modulatore utilizzato; invece, fmin = - K*(B/2).
Si definisce, inoltre, mf indice di modulazione pari a fmax / fm e quindi all’aumentare di
fm diminuisce il valore di mf e viceversa.
Si dimostra che:
VFM (t) = a* cospt+mf*senmt
Dove VFM (t) è il segnale modulato in frequenza; in base alle formule di Bessel, lo spettro in
frequenza della VFM (t) è simile a quelli di seguito riportato. Le ampiezze delle varie righe è pari a
Jn*A dove “n” aumenta man mano che ci si allontana dalla fp e si ricava, come gli stessi valori
delle J, dalle curve di Bessel (pag. 103 fig. 3.17 del libro); inoltre, le righe possono essere anche
negative, ma per semplicità di calcolo vengono spesso considerate tutte positive e la loro distanza
varia al variare della fm (se fm=cost. anche la loro distanze sono uguali).
A
Jo*A
J1*A
fp-fm
J1*A
fp
fp+fm
f
La RELAZIONE DI CARSON, invece, esprime il valore della BFM uguale a :
BFM = 2*(f+fm) = 2* (mf*fm+fm) = 2*fm*(mf+1)
Quindi, se mf<<1, si ha la cosiddetta “BANDA STRETTA” pari a BFM = 2*fm, mentre se mf>>1si
ha la “BANDA LARGA” pari a BFM = 2*fm*mf = 2*f.
I campi di impiego della tecnica FM è tra i 30 e i 300 MHz e tra i 300 e i 3000 MHz; quindi
con una f uguale a 75 Hz, la banda è 150 KHz, mentre la larghezza del canale è di 200 KHz.
La potenza totale della VFM è:
Pt = [(AJ0)2/2R]+ [(AJ1)2/2R]+ [(AJ2)2/2R]+ [(AJ3)2/2R]+……………..= (A2/2R)*(J0+ J0+ J0+…..)
ma siccome la somma di tutte le J è sempre 1 ( per le formule di Bessel), il tutto diventa:
Pt = A2/2R.
Se la Vm(t) non è sinusoidale, ogni riga dello spettro in frequenza visto prima risulta
formato da tante altre righe decrescenti in ampiezza man mano che ci si allontana dalla principale.
MODULATORI FM.
Per ottenere la VFM esiste il metodo DIRETTO (o della reattanza capacitiva o del diodo
varikap) e il metodo INDIRETTO (circuito di Amstrong). Il “modulatore con diodo varikap” è
quello qui sotto riportato:
Il diodo varikap si comporta come un condensatore variabile al variare della tensione inversa; in
pratica se la tensione inversa aumente, la zona di svuotamento della giunzione P-N del diodo
aumenta e di consguenza la sua capacità diminuisce. Il gruppo Co-Lo rappresenta l’oscillatore ad
alta frequenza, mentre il condensatore C serve isolare l’oscillatore dalle componenti continue. Il
valore della fp è pari a : fp = 1/[2**(Co*Lo)1/2] . Per il diodo varikap, maggiore è la tensione
inversa, minore è la capacità e quindi maggiore è la frequenza dell’oscillatore poiché la capacità del
diodo entra in gioco nella Co della formula della fp.
Se Vm (t) è nulla la fp sarà uguale a fpo = 1/[2**(Lo*(Cvo+Co)) ½]; ma quando la Vm(t)
varia anche la Cvo e quindi :
fp = 1/[2**(Lo*(Co+Cvo+cv)) ½] = fpo* [1+(cv/Co+Cvo)] -½
e, applicando quindi le formule matematiche il tutto diventa:
fp = fpo* [1-1/2*(cv/Co+Cvo)].
Esiste anche un altro circuito basato sul funzionamento del diodo varikap un po’ più
complicato e il circuito di Amstrong, i cui problemi sono le reti sfasatrici utilizzate.
DEMODULAZIONE FM.
Anche nella FM vi sono varie tecniche di demodulazione; la più importante è quella in grado
di convertire le f in variazioni di ampiezza in modo del tutto lineare per evitare situazioni più
problematiche. Si passa in pratica da una demodulazione FM ad una demodulazione AM tramite
circuiti detti “discriminatori” formato da un blocco L-C seguito da un rilevatore di inviluppo visto
in precedenza (il tutto a volte è seguito da un limitatore di ampiezza).
LIMITATORE
RILEV. DI
INVILUPPO
L-C
Matematicamente avremo:
FM = p+k*Vm(t)
VFM(t) = A*cosFM(t)
Dove FM(t) è un angolo del segnale modulato rispetto ad un riferimento ben preciso;
FM(t) = FM*dt poiché FM = d(t)/dt
Andando ora a sostituire:
FM(t) = p+k*Vm(t)*dt = p*dt +k*Vm(t)*dt = p*t + k*Vm(t)*dt
quindi:
VFM(t) = A*cos[p*t + k*Vm(t)*dt].
La tensione, invece, in uscita del blocco L-C risulta essere pari a :dVFM(t)/dt.
Il circuito sotto riportato è un discriminatore in cui gruppo L-C serve per accordarsi in frequenza
(per tale motivo C è variabile), il diodo per eliminare tutta la parte negativa ed il gruppo R-C
rappresenta il rilevatore di inviluppo visto già nella AM e che ha comunque gli stessi problemi
(taglio diagonale):
Tale circuito si comporta in realtà come un “circuito risonante parallelo” la cui frequenza di
Vc
Vc
f1 fp
f2
f
f di ris.
Variazioni di
frequenza
Variazioni dell’ampiezza di Vc(t)
in funzione della frequenza
t
risonanza è diversa dalla fp.
Il grafico in alto a sinistra rappresenta una curva di risposta di un circuito risonante parallelo, fp è la
frequenza portante di un generico segnale modulato, mentre f1 ed f2 sono rispettivamente il valore
minimo e massimo assunto dalla VFM(t) in frequenza; la Vc(t) del grafico di destra rappresenta
invece la tensione ai capi del condensatore variabile che rappresenta proprio la Vm(t) di partenza
come se fosse stata modulata in ampiezza (i problemi di tale circuito sono dovuti alla sua non
linearità supposta nella fase di studio).
Per migliorare tale tecnica di demodulazione si utilizza il “discriminatore bilanciato” che permette
di avere due campane di risonanza e suddividendo i suoi problemi su due circuiti invece di uno; la
fp questa volta coincide con il punto di incontro delle due campane mentre le due frequenza limite
su campane diverse.
Vc
fp
f1
f2
f
Var. d’amp.
Il circuito relativo è il seguente, e anche in questo caso il suo problema è quello della presa centrale
del trasformatore:
Nella realtà, però, i circuiti studiati fin ora che hanno solo uno scopo didattico sono sostituiti da
DISCRIMINATORI A RAPPORTO, A P.L.L., DI FOSTER-SEELY.
ESEMPIO DI SISTEMA DI MODULAZIONE IN FREQUENZA DIRETTA.
In trasmissione avremo:
VOCE
TRAS.
DRIVER
AMPL.
B. F.
AMPL.
di POT.
Classe C
MOD.
FM
OSCIL.
fp
TX
MOLT.
Di
FREQ.
SINTON.
AMPL.
RAD.FR.
AMPL.
B. F.
TRASD.
LIMIT.
DEMOD
FM
RX
Gli amplificatori di potenza in classe C a Bjt hanno campi di applicazione molto vasti e quindi
necessitano di una elevata tensione di eccitazione.
Il sintonizzatore è un circuito di accordo, mentre la fp in tal caso è compresa fra gli 88 e i
108 MHz. I circuiti che utilizzano i diodi varikap non possono provocare variazioni di frequenza
dell’ordine dei MHz e quindi vengono seguiti da blocchi moltiplicatori di frequenza o sostituiti da
altri componenti ( i moltiplicatori di frequenza, infatti, oltre a moltiplicare la fp moltiplicano anche
le f ).
Se il sistema viene migliorato in ricezione esso viene detto “sistema supereterodina”. Per
migliorare un sistema bisogna variare:
1. SENSIBILITA’: capacità di fornire determinate potenze;
2. SETETTIVITA’: capacità di selezionare due o più canali molto vicini tra di loro;
3. RAPPORTO S/N: esso dipende dalla sensibilità e determina la qualità del sistema;
4. FEDELTA’: capacità di riprodurre la Vm (t) in modo sempre più perfetto.
La fedeltà dipende da tutto il sistema e non da un singolo blocco, quindi dipende da una questione
del tutto economica.
Il sistema supereterodina permette di non demodulare direttamente il segnale ricevuto, ma effettua
prima una conversione frequenza-frequenza con cui la fp viene portata ad una frequenza intermedia
fi permettendo al selettore di lavorare in modo miglire. Quindi in definitiva, UN SISTEMA
SUPERETERODINA E’ PIU’ FEDELE.