LA DISTRIBUZIONE NORMALE
(Vittorio Colagrande)
Allo scopo di interpolare un istogramma di un carattere statistico X con una funzione
continua (di densità), si può far ricorso nell’analisi statistica alla distribuzione normale o
distribuzione di Gauss come modello teorico di riferimento. Ciò, in particolare, quando il
numero delle classi dell’istogramma è elevato e l’ampiezza di ogni classe piccola.
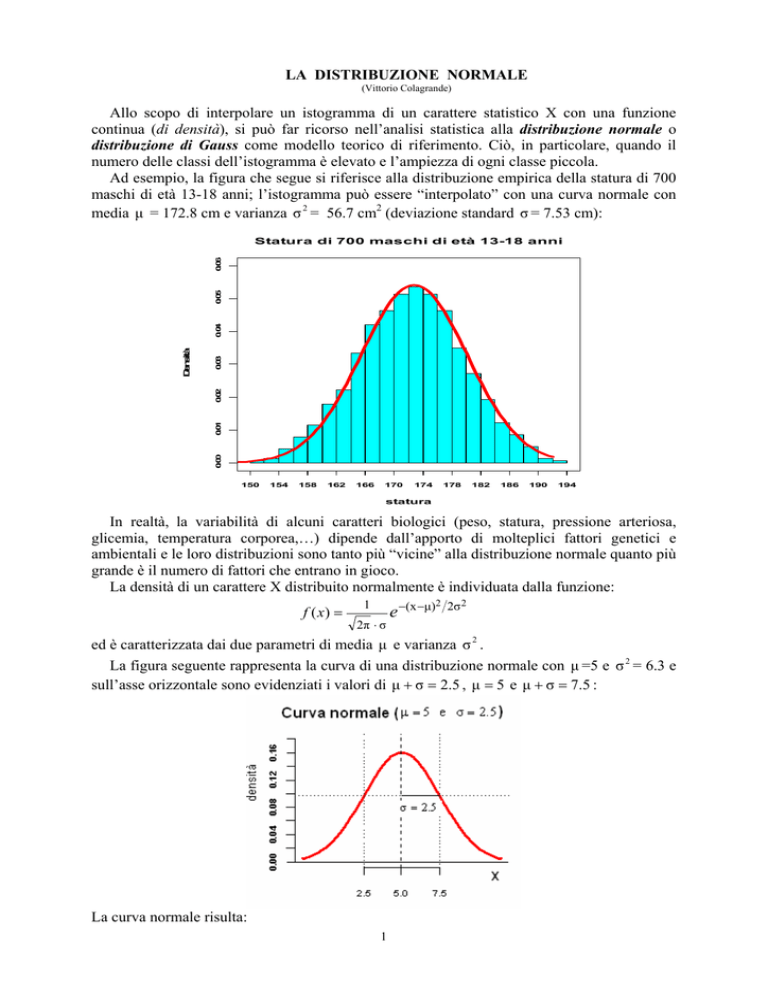
Ad esempio, la figura che segue si riferisce alla distribuzione empirica della statura di 700
maschi di età 13-18 anni; l’istogramma può essere “interpolato” con una curva normale con
media μ = 172.8 cm e varianza σ 2 = 56.7 cm2 (deviazione standard σ = 7.53 cm):
0.03
0.00
0.01
0.02
Densità
0.04
0.05
0.06
Statura di 700 maschi di età 13-18 anni
150
154
158
162
166
170
174
178
182
186
190
194
statura
In realtà, la variabilità di alcuni caratteri biologici (peso, statura, pressione arteriosa,
glicemia, temperatura corporea,…) dipende dall’apporto di molteplici fattori genetici e
ambientali e le loro distribuzioni sono tanto più “vicine” alla distribuzione normale quanto più
grande è il numero di fattori che entrano in gioco.
La densità di un carattere X distribuito normalmente è individuata dalla funzione:
f ( x) =
1
2π ⋅ σ
e −(x −μ)
2
2σ 2
ed è caratterizzata dai due parametri di media μ e varianza σ 2 .
La figura seguente rappresenta la curva di una distribuzione normale con μ =5 e σ 2 = 6.3 e
sull’asse orizzontale sono evidenziati i valori di μ + σ = 2.5 , μ = 5 e μ + σ = 7.5 :
La curva normale risulta:
1
•
•
•
simmetrica rispetto alla retta parallela all’asse verticale e passante per la media, ovvero,
presi due punti qualsiasi sull’asse orizzontale equidistanti dalla mediana (=media), uno a
sinistra e l’altro a destra, la funzione di densità assume per essi lo stesso valore;
asintotica rispetto all’asse delle ascisse, cioè per valori sempre più distanti dalla media
l’ordinata della curva tende a zero;
crescente nell’intervallo (−∞, μ ) e decrescente nell’intervallo (μ,+∞ ) ; la crescita è
“meno veloce” fino a μ − σ (punto di flesso) e più rapida da tale valore a μ ; si ha un
massimo in μ e poi l’andamento è decrescente con ritmo più veloce dal massimo a μ + σ
(punto di flesso).
Un significato importante assume l’area “al di sotto” della curva tra i valori X=x1 e X=x2:
Area tra x1 e x2 = Frequenza % dei valori di X compresi tra x1 e x2 = P(x1<X ≤ x2)
L’area totale al di sotto della curva è uguale a 1 e si può osservare che:
P(X>x1) = 1 ─ P(X ≤ x1) e P(x1<X ≤ x2) = P(X ≤ x2) ─ P(X ≤ x1).
La media è il parametro di posizione, nel senso che, al variare del suo valore, la curva non
cambia nella forma ma subisce una traslazione rispetto all’asse orizzontale; nella figura sono
rappresentate tre distribuzioni di pesi aventi la stessa varianza ma media diversa:
La varianza è il parametro di scala: al suo variare cambia la forma della curva di
distribuzione. In particolare, per bassi valori di σ , l’area sotto la curva è concentrata intorno
alla media, mentre per alti valori di σ , la curva è “schiacciata” rispetto all’asse orizzontale;
nella figura sono riportate tre distribuzioni di pesi aventi ugual media, ma varianze diverse:
2
Evidentemente esiste un numero infinito di distribuzioni normali diverse tra loro, ottenute
al variare dei due parametri. Tutte queste distribuzioni diverse possono essere ricondotte ad
un unica distribuzione standard: la distribuzione normale standard, avente media μ = 0 e
varianza σ 2 =1.
All’uopo va considerata la trasformazione (standardizzazione):
Z=
X −μ
,
σ
e Z è la variabile normale standardizzata e ha densità f ( z ) =
1
2π
e
−
z2
2
.
Graficamente:
Per il calcolo delle aree al di sotto della curva normale standardizzata si può far ricorso ad un
programma informatico (ad esempio all’ambiente R) o a tavole della distribuzione normale
standardizzata (come quella riportata in Appendice).
In merito alle aree, un risultato importante è schematizzato nella figura che segue:
3
Esempio 1. Una popolazione di maschi si distribuisce normalmente secondo la statura (X)
con media μ = 173 cm e deviazione standard σ =13 cm.
Determinare la frequenza relativa degli individui:
1. con statura maggiore di 200 cm;
2. con statura compresa tra 175 e 190 cm;
3. con statura minore di 156 cm.
Per rispondere alle domande poste è necessario procedere alla standardizzazione
dell’altezza e utilizzare la tavola riportata in Appendice.
1. standardizzando x = 200 cm:
200 − 173
z=
= 2.08 ,
13
si ha:
P(X>200) = P(Z>2.08) = 1 ─ P(Z ≤ 2.08) =
(ricercando all’interno della tavola nell’incrocio
tra la riga del 2.0 e la colonna di 0.08)
= 1─0.9812 = 0.019 = 1.9% ≅ 2% di individui;
2. standardizzando 175 e 190 cm:
175 − 173
190 − 173
z1 =
= 0.15 e z 2 =
= 1.31 ,
13
13
si ha:
P(175<X ≤ 199)=P(0.15<Z ≤ 1.31)=P(Z ≤ 1.31)–
–P(Z ≤ 0.15)= (valori interni alla tavola
nell’incrocio tra la riga di 1.3 e 0.01 e
nell’incrocio tra la riga di 0.1 e 0.05)
= 0.9049–0.5596 ≅ 35% di maschi;
4
3. standardizzando 156 cm:
156 − 173
z=
= −1.31 ,
13
risulta:
P(X ≤ 156)=P(Z ≤ ─1.31)=
(per
la
simmetria della curva) = P(Z >1.31) = 1 –
P(Z ≤ 1.31) = (valore interno alla tavola
nell’incrocio tra la riga 1.3 e la colonna
0.01) =1 – 0.9049 ≅ 10% di individui.
Sempre in riferimento all’esempio considerato, ci si può chiedere:
4. qual è la statura massima del 10% degli individui più bassi;
5. qual è la statura minima del 5% degli individui più alti.
Per rispondere alle due domande è necessario partire dai valori interni alla tavola (che sono
valori di frequenze relative/probabilità).
4. Va determinato, anzitutto, il valore z1 della variabile Z per il quale risulta
P(Z ≤ z1)=10%=0.1. Per la simmetria della curva (vedi grafico) risulta che: P(Z ≤ z1) =
P(Z>z2)=1–P(Z ≤ z2).Osservando all’interno
della tabella di Appendice, il valore z2 di Z al
quale corrisponde una probabilità di 0.90
(data da 1–0.1) è pari a 1.28 (riga di 1.2 e
colonna di 0.08). Pertanto, sempre per la
simmetria, si ha: z1=–1.28 e, per la
standardizzazione, il valore x1 della variabile
X corrispondente a z1 è dato da
(x1–
173)/13= –1.28 ⇒ x1 = 156 cm. Tale valore
è proprio la massima altezza del 10% degli
individui più bassi.
5. In questo caso il valore z1 di z è tale che P(Z>z1) = 5% = 0.05 e va determinato in modo
che risulti 1– P(Z ≤ z1) = 0.95. Dall’interno
della tavola si evince che il valore di Z al
quale corrisponde una probabilità del 95% è
pari a z1 = 1.645 (media dei valori di Z
corrispondenti al probabilità di 0.9495 e
0.9505). Il valore x1 dell’altezza di ottiene da:
(x1–173)/13= 1.645 ⇒ x1 = 194 cm, che
rappresenta proprio la statura minima del 5%
degli individui più alti nella popolazione presa
in esame.
Esempio 2. In una data popolazione è noto che l’HDL-colesterolo si distribuisce
normalmente con media μ = 57 mg/100ml e deviazione standard σ = 5 mg/100ml.
Determinare la percentuale di soggetti della popolazione con
a) HDL maggiore di 60 mg/100ml,
b) HDL compreso tra 40 e 45 mg/100ml,
c) HDL minore di 58 mg/100ml,
d) HDL tra 55 e 58 mg/100ml.
(risultati: a) 27.43%, b) 0.79%, c) 57.93%, d) 23.47%).
5
APPENDICE
6










