Capitolo 4
NMR – REOLOGIA
4.1 Introduzione
Dalla reologia si possono registrare gli effetti che la struttura del
materiale ha sul suo comportamento macroscopico e meccanico, gli studi
dei tempi di rilassamento del protone 1H provenienti dagli spettri NMR a
basso
campo
permettono
di
indagare
sulle
loro
caratteristiche
microscopiche. L’insieme delle due informazioni porta alla determinazione
della distribuzione dei diametri dei pori del reticolo polimerico.
Per comprendere appieno il significato fisico di quest’affermazione è
ora necessario spostare l’attenzione sulla caratterizzazione reologica dei
gel: le prove reologiche effettuate per questi sistemi prevedono prove di
stress sweep lungo per indicare il campo di viscoelasticità lineare. Una
volta individuato il campo di viscoelasticità lineare, vengono effettuate le
prove di frequency sweep.
Il fitting dello spettro meccanico del gel (determinato mediante prove
di frequency sweep) mediante il Modello di Maxwell generalizzato permette
di stabilire quanti siano gli elementi viscoelastici necessari per la
correlazione dei dati sperimentali. Assumendo che il modulo di taglio (G)
del gel sia dato dalla somma dei contributi elastici di tutti gli elementi di
Maxwell necessari per il fitting dello spettro meccanico, è possibile risalire
alla densità di reticolazione ρx dei gel in esame mediante la teoria di Flory
[1]:
ρ x = G ν 2p 3 RT
(4.1)
dove R è la costante universale dei gas, T è la temperatura assoluta
e νp è la frazione volumetrica di polimero nel gel. Basandosi sulla
conoscenza di ρx è possibile stimare la dimensione media (ϕ) delle maglie
NMR - Reologia
del reticolo polimerico secondo quanto previsto dalla teoria del network
equivalente [2]:
φ = 3 6 (π N av ρ x )
(4.2)
dove Nav è il numero di Avogadro. Calcolato ϕ, è possibile combinare
questa informazione con quelle provenienti dall’indagine NMR. Infatti, si
può desumere la distribuzione delle dimensioni delle maglie del reticolo
polimerico, sapendo che il tempo di rilassamento trasversale T2 degli
idrogeni dell’acqua confinata nei nanopori (le maglie del reticolo
polimerico) è uguale al prodotto del diametro medio del poro per una
costante k che dipende dalla geometria del poro (sferico, cilindrico, etc.) e
dalla natura chimica della superficie interna del poro (qua inteso come
maglia del reticolo) [3]. La determinazione di k discende direttamente
dalla definizione di tempo di rilassamento medio ( T 2 ) di uno o più picchi:
k ξ max
T2 max
∫ a(T ) * T
2
T2 =
2
* dT2
T2 min
T2 max
∫ a(T ) * dT
2
T2 min
2
T2 = kξ
}
=
k
∫ a(ξ ) * ξ * dξ
2
kφ min
kφ max
k
eq.(2)
}
= kφ = k3
∫ a(ξ ) * dξ
6
π N av ρ x
(4.3)
kξ min
dove a indica l’intensità locale di uno o più picchi dello spettro NMR
a basso campo, T2max (o ξmax) e T2min (o ξ2min) indicano l’estensione di uno o
più picchi in termini di tempo di rilassamento T2 (o diametro della
maglia). Dunque, k si misura in (ms/nm). E’ quindi possibile convertire T2
in diametri ed assegnare una distribuzione differenziale normalizzata del
poro con diametro ϕ nell’ambito del reticolo polimerico.
4.2 Densità di reticolazione
I punti di reticolazione dei reticoli polimerici o networks polimerici
sono caratterizzati, dalla densità di reticolazione ρ x che indica le moli di
punti reticolazione per unità di volume valutato sul gel secco, cioè in
assenza del solvente che lo rigonfia. Si può dimostrare che ρ x
80
è
Capitolo 4
inversamente proporzionale al peso molecolare medio per unità di
crosslinking o punto di reticolazione, M c :
ρx =
1
νMc
(4.4)
In cui ν è il volume specifico (volume/massa) del polimero.
Nei gel, la conoscenza della densità dei punti di reticolazione o
densità di crosslinking è di grande importanza, poiché essa influenza le
proprietà meccaniche di questi materiali ed il suo comportamento quando
utilizzati in diverse applicazioni pratiche, tra cui quelle biomediche.
Secondo
la
teoria
di
Flory
[4],
un
reticolo,
non
solvatato
inizialmente, rigonfia grazie all’assorbimento del solvente fino a quando
l’aumento dell’energia elastica delle catene che formano il network
polimerico
bilanciano
la
diminuzione
d’energia
libera
di
Gibbs
conseguente al mescolamento dei segmenti polimerici con le molecole di
solvente. La condizione d’equilibrio così raggiunta, si può esprimere
mediante la seguente equazione:
2
1
2
v [ln( 1 − v 2 , s ) + v 2 , s + χ 1v 2 , s ]
=
−
v
Mc
M n V1
[v1 3 − 2, s ]
2,s
2
(4.5)
dove v 2 , s , è la frazione volumetrica finale del polimero nello stato
rigonfiato, all’equilibrio termodinamico;
V 1 , è il volume molare di
solvente; v , è il volume specifico del polimero nello stato amorfo; M n , è il
peso molecolare medio numerico delle catene principali del polimero
mentre χ 1 è il parametro d’interazione polimero – solvente di Flory.
L’equazione di cui sopra, è stata modificata da Flory [5] per il caso
di networks già rigonfiati, vale a dire, reticoli polimerici dove la
reticolazione viene creata nel polimero che si trova in soluzione e non allo
stato secco. Lo stato da prendere come stato di riferimento quindi, è
quello in cui il polimero viene reticolato in soluzione occupando la
frazione volumetrica v 2 , r prima che venga messo a contatto con nuovo
81
NMR - Reologia
solvente e raggiunga con esso un nuovo equilibrio. In questo caso,
l’equazione che descrive l’equilibrio di rigonfiamento è:
2
v [ln( 1 − v 2 , s ) + v 2 , s + χ 1v 2 , s ]
1
2
=
−
v
1 v
Mc
M n V1
v 2 , r [( 2 , s )1 3 − ( 2 , s )]
v2 , r
2 v2, r
(4.6)
La teoria dell’elasticità delle gomme, Flory et al. [6], dice che,
quando un polimero reticolato, inizialmente secco, viene rigonfiato in
modo tale che la frazione volumetrica di polimero decresce fino a
raggiungere la frazione volumetrica v 2 , lo sforzo di taglio τ (espresso come
forza per unità di superficie del campione rigonfiato) ad esso applicato è
legato al rapporto di allungamento α = l l 0 ; ( l 0 , l , lunghezza iniziale e
finale del campione rispettivamente) dalla la seguente espressione:
τ
2
α − (1 α )
=
2M c 1 3
RT
(1 −
)v 2
vM c
Mn
(4.7)
Per il caso in cui il polimero venga reticolato in soluzione alla
concentrazione in peso C2,r [gr/cm3] e successivamente ulteriormente
rigonfiato, l’equazione (4.7) di cui sopra si modifica, e si ottiene la
seguente relazione [6]:
τ
2
α − (1 α )
C 2.r
2M c
(1 −
) Q −1 3
Mc
Mn
= RT
Q2 = v2 r v2 s
(4.8)
(4.9)
dove Q è il, rapporto volumetrico di rigonfiamento. La densità di
reticolazione per questi sistemi è espressa da:
ρx =
C 2.r
2M c
(1 −
)
Mc
Mn
(4.10)
La (4.8) può essere scritta in forma più semplice non appena ci si
limiti al caso di piccole deformazioni (campo viscoelastico lineare). Infatti,
si ha:
α − (1 α 2 ) = (α − 1)
α 2 +α +1
α2
(4.11)
Detta ε = (α − 1) la deformazione, la (4.11) può essere facilmente
manipolata come segue:
82
Capitolo 4
α − (1 α 2 ) = (α − 1)
α 2 +α +1
1
1
= ε (1 + 2 + )
2
α
α
α
(4.12)
da cui, si perviene a:
α − (1 α 2 ) = ε (1 +
1
α
2
+
1
α
≅α →1
)
3ε
(4.13)
Se
,
Viscoelasticità
Lineare
per piccole deformazioni. Dunque, la (4.8) diventa:
τ
= ρ x Q −1 3 RT
3ε
(4.14)
τ = ε 3 ρ x Q −1 3 RT
(4.15)
Pertanto, il modulo di Young E sarà dato da:
E = 3 ρ x Q −1 3 RT
(4.16)
Ricordando la relazione esistente, in regime viscoelastico lineare, tra
il modulo di Young e quello di taglio G ( E = 3G ), si ha:
E = 3 ρ x Q −1 3 RT
(4.17)
G = ρ x Q −1 3 RT
(4.18)
Se non c’è rigonfiamento Q = 1 . Pertanto:
G = ρ x RT ;
E = 3 ρ x RT
(4.19)
Per chiarire meglio questi concetti, supponiamo di formare un gel
reticolando una soluzione polimerica in cui la frazione volumetrica di
polimero sia v 2 , 0 . S’immagini ora di rigonfiare ulteriormente il gel
portandolo dal volume iniziale V 0 al volume finale rigonfiato V . Sia v 2 la
frazione volumetrica del polimero in queste condizioni. Si supponga ora
che il gel sia sottoposto a deformazione (compressione o allungamento)
nella direzione x rispetto ad un sistema cartesiano di assi coordinati x, y,
z, e tale deformazione avvenga a volume costante.
Siano α x =
x
y
z
, αy =
, α z = , le variazioni di lunghezza nelle
x0
y0
z0
direzioni x, y, z dovute all’effetto combinato dello swelling e della
deformazione (x0, y0 e z0 indicano le dimensioni del gel prima del
rigonfiamento e della deformazione meccanica). Ovviamente si ha che:
83
NMR - Reologia
x y z
xyz
xyz
1
=(
)( s s s ) =
.v 20
x0 y0 z0
x s y s z s x0 y0 z 0
v2
α xα y α z =
(4.20)
dove V s = x s y s z s è il volume occupato dal solo polimero (ovvero il gel
privato della componente rigonfiante).
Ma, essendo lo swelling isotropo, si ha che:
x0 s y 0 s z 0 s
=
=
x0
y0
z0
e quindi,
(4.21)
la variazione di volume del gel dovuta allo swelling
isotropo è:
x y z
x
v
V
= 0 s 0 s 0 s = ( 0 s ) 3 = 20
V0
x0 y 0 z 0
x0
v2
(4.22)
Combinando gli effetti della deformazione dovuta allo swelling
isotropo con quelli dovuti alla deformazione meccanica, la variazione di
lunghezza lungo l’asse x diventa:
swelling
isotropo
678
x
α x = 0 s
x0
x
0s
1x2
3
(4.23)
α
allungamento
meccanico
Immettendo la (4.22) nella (4.23) si ha:
13
V
α x = α
V0
v
α x = α 20
v2
(4.24)
13
(4.25)
Poiché, per simmetria, α y = α z , la (4.20) diventa:
(α z )2 α x
=
v 20
v2
(4.26)
Ricordando la (4.25), la (4.26) diventa:
13
(α z )
2
v
v 1v
= 20 = 20 2
v2α x v2 α v20
1 v
= 20
α v2
da cui:
84
23
(4.27)
Capitolo 4
1 v 20
αz = αy =
α v 2
23
Dal
vista
punto
di
v
= 20
v2
13
1
(4.28)
α
termodinamico,
la
variazione
d’entropia
configurazionale dovuta all’effetto combinato dello swelling e della
deformazione è data dall’equazione [1]:
23
23
v
κν e 2 v 20
2 v 20
+
− ln 20
α
∆S = −
α v2
2 v2
v 2
(4.29)
In cui κ è la costante di Boltzman e ν e indica il numero dei punti di
reticolazione. Ricordando che la forza elastica di richiamo per una gomma
ideale è [1]:
f =−
T ∂S
xos ∂α T ,V
(4.30)
Combinando la (4.29) con la (4.30) si ha:
23
T κν e v 20
2
−
− 2
2α
f =−
xos 2 v 2
α
Tκν e
1 v 20
f =
α − 2
xos
α v 2
v 20
v2
23
(4.31)
23
(4.32)
Dividendo f per y os * z os (superficie rigonfiata non deformata), si ha
la tensione per unità di superficie rigonfiata non deformata:
τ=
f
y osy z os
Tκν e
=
xos y osy z os
1
α − 2
α
v 20
v 2
23
(4.33)
Ricordando che:
xos y osy z os =
ν=
νe
N
v 20
V0
v2
4.34
(4.34’)
dove ν rappresenta il numero di moli di punti di reticolazione ed N
è il numero di Avogadro, la (4.33) diventa:
85
NMR - Reologia
v
1
τ = NκT 2 α − 2
V0
v 20
α
ν
v 20
v 2
23
v
1
= RT α − 2
V0
α
{
v 2
v 20
13
(4.35)
ρX
Poiché si è visto precedentemente (eqs. (4.11)-(4.13)) che per piccole
deformazioni ε il termine α − (1 α 2 ) ≈ 3ε , la (4.35) diviene:
v
τ = RTρ X 3ε 2
v 20
13
(4.36)
Essendo lo sforzo di taglio
τ
legato alla deformazione attraverso il
modulo di Young E secondo τ = Eε , allora, attraverso la (4.35), il modulo di
Young può essere espresso come:
13
v
E = 3RTρ X 2
v20
(4.37)
Poiché nell’ambito viscoelastico lineare il modulo di taglio G e di
Young E sono proporzionali tra loro secondo E = 3G [7], si ha:
v
G = RTρ X 2
v 20
13
(4.38)
Se non si ha rigonfiamento della matrice ( v 2 = v 20 ) prima della
sollecitazione meccanica, entrambi i moduli diventano:
Modulo di Taglio
(4.39)
E = 3RTρ X Modulo di Young
(4.40)
G = RTρ X
4.3 Risonanza Magnetica Nucleare (NMR)
I fondamenti fisici della spettroscopia di Risonanza Magnetica
Nucleare (NMR) si basano sulle proprietà magnetiche dei nuclei atomici
[8]. In accordo con le regole della meccanica quantistica, l’interazione del
momento magnetico di un nucleo con un campo magnetico esterno (B0)
porta alla separazione dei livelli energetici nucleari. Questo perché
l’energia magnetica del nucleo è ristretta a certi valori discreti Ep
chiamati autovalori, ai quali sono associati gli autostati, che sono i soli
stati in cui può esistere una particella elementare. Questi sono anche
chiamati stati stazionari. Operando con una radiazione elettromagnetica
86
Capitolo 4
di frequenza opportuna, è possibile indurre transizioni tra gli autostati:
l’assorbimento di energia può essere rilevato e registrato come riga
spettrale (segnale di risonanza).
In questo modo si può ottenere lo spettro di un composto che
contiene atomi i cui nuclei possiedono un momento magnetico diverso da
zero. Tra questi vi sono il protone, 1H, il fluoro,
19F,
gli isotopi
14N
e
15N
dell’azoto, e molti altri nuclei di interesse.
4.3.1 Modello quantomeccanico per un nucleo isolato
È noto dalla fisica nucleare che molti nuclei atomici possiedono
momento angolare, P, che a sua volta è responsabile del fatto che questi
nuclei esibiscono anche un momento magnetico, µ . Le due quantità sono
correlate dall’espressione:
µ = γP
Dove
(4.41)
γ , il rapporto giromagnetico, è una caratteristica del
particolare nucleo. Secondo la teoria quantistica, momento angolare e
momento magnetico nucleare sono quantizzati, un fatto che non è
spiegato dalla fisica classica. I valori permessi o autovalori della
componente massima del momento angolare nella direzione z di un
sistema di coordinate cartesiane scelto arbitrariamente sono definiti dalla
relazione:
Pz =
h
mI
2π
dove µ = γ P
(4.42)
è il numero quantico magnetico che caratterizza i
corrispondenti stati stazionari o autostati del nucleo ed h è la costante di
Planck. In accordo con la condizione quantistica:
m I = I , I − 1, I − 2 ,..., − I
(4.43)
i numeri quantici magnetici sono correlati al numero quantico di
spin, I, del nucleo. Pertanto il numero totale di autostati o livelli di energia
possibili è:
Numero livelli energetici = 2 I + 1
87
(4.44)
NMR - Reologia
Il protone ha un numero quantico di spin I = 1
2
e quindi la
componente z del suo momento angolare è data dalla:
Pz = ±
h
I
2π
(4.45)
Di conseguenza il protone può esistere in solo due stati di spin
caratterizzati dai numeri quantici magnetici m I = + 1
2
e m I = − 1 . Per
2
quanto riguarda il valore del momento magnetico nella direzione z si ha:
µz = γ
h
mI = ±γ h
4π
2π
(4.46)
Il protone può quindi essere raffigurato come un dipolo magnetico
la cui componente z, µ z , può essere parallela o antiparallela rispetto alla
direzione positiva dell’asse z del sistema di coordinate cartesiane.
Pertanto la direzione del vettore µ è quantizzata come è mostrato in
figura 4.1 (a):
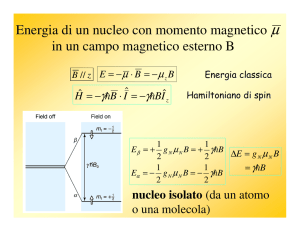
Figura 4.1. (a) Direzione quantizzata del vettore µ in assenza del campo
magnetico Bo. (b) Interazione del momento magnetico nucleare µ con Bo.
In assenza di un sistema orientante, i due stati hanno la stessa
energia, cioè sono degeneri. La degenerazione viene rimossa soltanto in
un campo magnetico B0 e questo avviene a causa dell’interazione del
momento magnetico nucleare µ con B0. Se la direzione di B0 coincide con
l’asse z, come in Figura 4.1 (b), la differenza di energia tra i due stati di
spin risulta essere:
∆E = 2 µ z Bo
(4.47)
88
Capitolo 4
Perché l’energia di un dipolo magnetico nel campo Bo è − µ z Bo ,
quando il dipolo è orientato parallelamente al campo, e + µ z Bo , quando è
orientato in opposizione (figura 4.2), si vede che la separazione d’energia
tra i due stati è proporzionale all’intensità del campo magnetico applicato.
Figura 4.2. Separazione d’energia ∆E tra due stati, proporzionale al campo
magnetico applicato.
Vista la sua minore di energia, lo stato m I = + 1
2
è il più stabile e
per indurre transizioni verso il livello ad energia più alta bisogna fornire il
quanto d’energia
∆E = hν o = 2 µ z Bo = γ
h
Bo
2π
(4.48)
Ossia si deve usare una radiazione di frequenza:
ν o = γBo 2π
(4.49)
Oppure:
ω o = γBo
(4.50)
in cui ω = 2πν
L’equazione di cui sopra, che esprime la condizione di risonanza,
rappresenta la situazione in cui la frequenza della radiazione coincide
esattamente con la differenza di energia fra i due stati. La riga spettrale
corrisponde alla freccia in figura 4.2 e ν o (o ω o ), la frequenza di Larmor,
in accordo con l’equazione 4.49 (oppure 4.50), varia linearmente con
l’intensità del campo Bo usato nell’esperimento. Ad esempio per i protone,
89
NMR - Reologia
che ha un rapporto giromagnetico γ H = 2.675 × 10 8 T −1 sec −1 , un campo di
1.41 T porta la frequenza di Larmor a 60 MHz ( λ = 5 metri, regione delle
onde radio). Valori di ν o a vari campi sono mostrati in Figura 4.3.
Figura 4.3. Separazione dei livelli energetici nucleari del protone (espressi
come frequenza di risonanza
νo )
in funzione del campo magnetico, espresso in
Tesla.
Per un nucleo con I=1 spin, vi sono tre livelli di energia, come si
osserva in figura 4.4:
Figura 4.4. A sinistra, separazione dei livelli energetici (2) di un nucleo con
numero quantico di spin I=1/2 in presenza di Bo; a destra, la separazione dei livelli
energetici (3) di un nucleo con I=1.
Per sistemi con I ≥ 1 , il trattamento quantomeccanico fornisce un
risultato non previsto dalla fisica classica: si trova che il numero quantico
magnetico m I può variare soltanto di ± 1 , cioè che sono permesse solo
transizioni tra livelli adiacenti. Così, nel caso di un nucleo con I = 1 , sono
90
Capitolo 4
possibili le transizioni tra i livelli m = +1 e m = 0 e tra i livelli m = 0 e
m = −1 , mentre non sono permesse quelle tra i livelli m = +1 e m = −1 .
Da quanto visto, si deduce che i valori dei momenti magnetici
nucleari possono essere specificati in termini del rapporto giromagnetico
definito come:
γ =
2πµ
Ih
(4.51)
Si può dimostrare inoltre che una particella sferica rotante di massa
M e con una carica e distribuita uniformemente sulla superficie genera
un momento magnetico
µ=
eh
4πMc
(4.52)
dove c è la velocità della luce. Per una particella che ha la massa e
la carica del protone si calcola:
µN =
eh
= 5.0505 × 10 − 27 joules / tesla ( J T −1 )
4πMc
(4.53)
Nella realtà si trova che il valore del momento magnetico è di circa
2.79 volte più grande di quello calcolato con questo modello semplificato.
Non esistono modelli semplici che permettono di predire o di
spiegare i valori dei momenti magnetici nucleari. Tuttavia il valore
calcolato per il protone rappresenta un’unità di misura utile per
esprimere i momenti magnetici nucleari ed è nota col nome di magnetone
nucleare, µ N . I valori osservati dei momenti magnetici nucleari possono
essere specificati in termini del magnetone nucleare usando la relazione:
µ = gN
ehI
4πMc
(4.54)
dove g N è un parametro empirico chiamato fattore g nucleare.
Pertanto, in unità di magnetoni nucleari, µ N , si ha:
µ = gN I
(4.55)
In tabella 4.1 i momenti magnetici sono espressi in queste unità.
91
NMR - Reologia
Tabella 4.1. Proprietà di alcuni nuclei di interesse in spettroscopia NMR.
4.3.2
Meccanismo
dell’assorbimento
di
energia
(Risonanza)
I nuclei con spin I = 1 2 , come i protoni
1H,
vengono spesso
raffigurati come delle barrete magnetiche. Tuttavia a causa del moto di
spin, il loro comportamento è diverso da quello manifestato dalle barre
magnetiche macroscopiche.
Figura 4.5. (a) Trottola che precede nel campo gravitazionale terrestre; (b)
Precessione di un momento nucleare in un campo magnetico.
Quando sono posti in un campo magnetico, i nuclei rotanti non
allineano i loro momenti magnetici nella direzione del campo. Al contrario,
92
Capitolo 4
come trottole in un campo gravitazionale (Figura 4.5a), i loro assi di spin
subiscono un moto di precessione intorno alla direzione del campo
(Figura 4.5b).
La frequenza di precessione è la frequenza di Larmor indicata con
ω o , in radianti per secondo, o con ν o , in Hertz (Hz, cicli per secondo):
ω o = γBo (8)
(4.56)
Se si cerca di forzare l’allineamento di µ aumentando l’intensità del
campo magnetico Bo , si ottiene soltanto una precessione più veloce.
Tuttavia è possibile far variare l’orientazione di µ applicando un campo
magnetico rotante B1 perpendicolare a Bo (Figura 4.6).
Figura 4.6. L’orientazione di
µ
applicando un campo magnetico rotante
perpendicolare a
B1
Bo .
Quando la frequenza di rotazione di B1 , ν RF , coincide esattamente
con la frequenza di precessione ν o (condizione di risonanza), il sistema
assorbe energia e cambia l’angolo θ tra il vettore µ ed il campo magnetico
statico Bo . Il processo avviene senza variazioni del valore di ν o .
4.3.3 Magnetizzazione macroscopica
93
NMR - Reologia
In un esperimento NMR non si tratta mai un singolo momento
nucleare, ma si studia sempre un insieme contenente un numero molto
grande di nuclei identici. Di conseguenza, per descrivere le proprietà della
magnetizzazione nucleare (momento magnetico per unità di volume del
campione),
si
può
usare
un
semplice
trattamento
classico.
La
magnetizzazione, M , è una quantità vettoriale le cui componenti sono
M z , per definizione secondo la direzione di Bo , e M x e M y perpendicolari
a Bo . In figura 4.7 è mostrata la precessione di un insieme di nuclei
identici con spin I = 1 2 . Tutti i momenti precedono alla stessa frequenza;
poiché non c’è modo di distinguere tra loro le direzioni x e y , non c’è
ragione per una coerenza di fase nel piano xy , allora M xy = 0 .
Figura 4.7. (a) Precessione di un insieme di momenti magnetici identici di
nuclei con I=1/2. Tutti i vettori sono considerati con origine comune. La differenza
di popolazione è mostrata da un eccesso di spin orientati secondo Bo (direzione +
z), e si produce così una magnetizzazione netta Mz. Non c’è coerenza di fase e
quindi Mxy = 0. (b) Sistema di spin in coerenza di fase, Mxy diverso da zero.
Poiché la distribuzione di Boltzmann favorisce leggermente lo stato
a più bassa energia, all’equilibrio vi sarà un eccesso di nuclei allineati
nella direzione di Bo (figura 4.8):
94
Capitolo 4
Figura 4.8. Eccesso di nuclei allineati nella direzione di Bo.
E questa differenza di popolazione genera una magnetizzazione
macroscopica netta M z (figura 4.7 a):
M z = γh( N 1 − N 2 )
(4.57)
L’applicazione del campo di radiofrequenza (RF) B1 rotante alla
frequenza di risonanza ω o = γBo
fa sì che gli spin risuonino e di
conseguenza la distribuzione causale delle orientazioni nel piano xy viene
modificata ed appare una componente M xy ≠ 0 . Sistemi di spin che danno
origine a componenti nette della magnetizzazione nel piano xy sono in
coerenza di fase (figura 4.7b).
4.3.4 NMR a basso campo
Gli spettri NMR a basso campo o spettri a linee larghe sono quelli in
cui ampiezza della linea di risonanza osservata è molto più larga rispetto
alle linee di risonanza che producono gli ambienti chimici che circondano
il nucleo osservato.
Per questo motivo, l’indagine NMR a basso campo apporta
informazioni relative alla concentrazione e all’intorno fisico di un isotopo
osservato. La tecnica può essere applicata tanto a campioni solidi come
liquidi, sospensioni, sistemi gel, emulsioni, non è una tecnica distruttiva,
è indipendente dal colore e dalla superficie del campione. Il campo di
indagine è tra i 10-65 MHz, a temperature che variano da -10 a + 70 °C
(precisione 0.02 °C).
L’ampiezza e la forma delle linee di risonanza sono indicative
dell’ambiente fisico che circonda all’isotopo. In particolare, l’ampiezza
della linea di risonanza rivela il grado di libertà di movimento dell’isotopo
95
NMR - Reologia
in quello specifico ambiente fisico, informazione che si rivela molto
importante negli studi della chimica dei polimeri, così come nella fisica
dello stato solido. Dal punto di vista qualitativo, il tempo di rilassamento
di un nucleo dipende dalla propria mobilità. Nei solidi, si ha una ridotta
mobilità e quindi un tempo di rilassamento trasversale T2 veloce (1-100
ms); nei campioni dove si ha una mobilità media come nel caso dei gel, il
tempo di rilassamento T2 è medio, (200-800 ms), infine nei liquidi la
mobilità dei nuclei è alta e quindi, il tempo di rilassamento è lento (800 e
2500 ms).
NMR a basso campo trova un vasto impiego in diverse aree, dalla
scienza e tecnologia degli alimenti, in molte applicazioni industriali e nel
campo farmaceutico e della cosmetica. Si tratta di un metodo veloce, non
distruttivo, per analizzare il contenuto protonico in grassi e oli, così come
la determinazione d’umidità o il contenuto d’acqua in molti tipi di
materiali.
Una delle recenti applicazioni trova spazio nell’analisi quantitativo
di materiali, orientato in particolare a determinare il contenuto di un
isotopo particolare mediante l’integrazione dell’area sotto il segnale di
assorbimento.
Per quanto riguarda gli idrogel, nel dominio del tempo di uno
spettro NMR del protone 1H, possono riconoscersi e distinguersi diversi
tipi di fasi presenti nel campione:
Figura 4.9. Spettro di rilassamento del protone 1H tipico di un idrogel non
omogeneo.
96
Capitolo 4
4.3.5 L’esperimento NMR
Al campione è applicato un forte campo magnetico statico Bo .
Questo campo deve essere molto omogeneo e, per migliorare l’omogeneità,
spesso il campione viene fatto ruotare intorno al suo asse verticale. Per
generare coerenza di fase tra gli spin si deve applicare un campo
magnetico rotante in direzione normale a Bo . Il campo rotante B1 , è
applicato attraverso una spira sintonizzata. Si generano così componenti
M xy della magnetizzazione che precedono alla frequenza ω o . Un processo
di rilassamento fa perdere la coerenza di fase e, dopo un certo tempo,
viene raggiunta la posizione di equilibrio dove M xy = 0 . Questo processo di
rilassamento porta ad un decadimento esponenziale di M xy con una
costante di tempo T2 (tempo di rilassamento trasversale o spin-spin). Il
risultato finale è un segnale transiente con frequenza ω o e velocità di
decadimento 1 T2 . Normalmente questo segnale viene chiamato FID (free
induction decay).
Figura
4.10.
Rappresentazione
schematica
dell’esperimento
campione è posto in una spira sintonizzata alla frequenza di risonanza.
97
NMR.
Il
NMR - Reologia
Se vi sono molti segnali con differenti valori di ω o e di 1 T2 , il FID,
che è un sovrapposizione di tutti i segnali, sarà più complicato.
Tuttavia può essere risolto usando un metodo matematico noto
come trasformata di Fourier (FT), che cambia il segnale transiente in un
normale spettro. Si deve notare che uno spettro è un diagramma
dell’intensità contro la frequenza (figura 4.11 (b)), mentre il FID è un
diagramma dell’intensità contro il tempo (figura 4.11 (a)). Il dominio dei
tempi ed il dominio delle frequenze sono collegati tra loro dalla
trasformata di Fourier.
Figura 4.11. (a) FID di due segnali NMR; (b) Lo spettro che si ottiene dal FID
operando la trasformata di Fourier.
Un concetto importante utilizzato quando si applica il metodo
transiente è quello che porta a definire in termini di angoli l’impulso del
campo applicato B1 . È stata discussa la precessione alla frequenza ω o in
un campo Bo . L’idea della precessione può essere anche estesa al caso del
campo rotante B1 per mezzo dell’espediente che utilizza un sistema di
riferimento rotante alla stessa frequenza di B1 . Rispetto a tale sistema di
riferimento B1 diventa statico a tutti gli effetti. Nell’istante in cui è
applicato B1 si ha la situazione mostrata in figura 4.12a, con B1 lungo
l’asse rotante x’ e la magnetizzazione di equilibrio, M o , lungo z. la
componente M o precede intorno a B1 proprio come i momenti magnetici
nucleari µ precedono intorno a Bo . La frequenza di precessione di M o è
98
Capitolo 4
ω1 = γB1 . Poiché ω (rad/sec) è una frequenza angolare, si vede che l’angolo
θ di cui è ruotata M o è dato da
θ = γB1t p
(4.58)
dove t p è il tempo di applicazione dell’impulso del campo B1 . Dopo
un impulso a 90° si ha M xy = M o (figura 4.12b), mentre dopo un impulso a
180° si ha M z = − M o e M xy = 0 (figura 4.12c).
Figura 4.12. Effetto dell’applicazione di un campo magnetico rotante B1
sulla magnetizzazione Mo, x’ e y’ sono coordinate che appartengono ad un sistema
di riferimento rotante alla stessa frequenza di B1. (a) Al tempo zero; (b) Situazione
dopo un impulso a 90°; (c) Dopo un impulso a 180°.
È possibile valutare l’effetto di un impulso di radiofrequenza sulle
popolazioni dei livelli nucleari quantizzati.
Si consideri un sistemi con soli due livelli α e β (figura 4.13.a), e si
supponga che vi siamo complessivamente N nuclei che possono essere in
uno stato o nell’altro.
Figura 4.13. A sinistra, popolazioni iniziali di un sistema a due livelli; a
destra effetto di un impulso che ruota la magnetizzazione di un angolo θ (angolo di
flip).
99
NMR - Reologia
Se i due livelli fossero degeneri, allora vi sarebbero N/2 nuclei per
parte, ma poiché lo stato α ha energia un po’ più bassa esso avrà un
leggero eccesso di popolazione. Se nello α vi sono δ nuclei più che in β ,
allora le rispettive popolazioni saranno ( N + δ ) / 2 e ( N − δ ) / 2 .
Per calcolare cosa succede alle popolazioni quando viene applicato
un impulso di radiofrequenza capace di far deflettere la magnetizzazione
macroscopica di un angolo θ , focalizziamo l’attenzione sulla componente
M z . È conveniente considerare le popolazioni in eccesso, cioè le deviazioni
da N / 2 , Pα e Pα degli stati α e β , che all’inizio valgono rispettivamente
+δ /2 e −δ /2.
In ogni istante la componente z della magnetizzazione, M z , è
proporzionale alla differenza di popolazione tra i livelli:
(4.59)
M z ∝ Pα − Pβ
Così all’inizio è M o ∝ δ . Inoltre sappiamo che deve essere
Pα + Pβ = 0
(4.60)
Dopo l’impulso θ , la componente z della magnetizzazione è (si veda figura
4.11.a)
M z = M o cos θ
(4.61)
E di conseguenza si ha:
Pα − Pβ = δ cos θ
(4.62)
Combinando con la 4.60, si calcolano le nuove popolazioni:
Pα =
Pβ =
δ cos θ
2
− δ cos θ
2
(4.63)
(4.64)
Queste ultime ci permettono di correlare quanto abbiamo già visto
riguardo agli impulsi
π 2
e
π con quello che succede nei livelli
quantizzati. Se θ = π 2 , allora cos θ = 0 e non vi è più eccesso di
100
Capitolo 4
popolazione in ciascun stato, cioè l’impulso di radiofrequenza eguaglia le
popolazioni. Se θ = π , allora cos θ = −1 , e le popolazioni sono invertite.
Quanto detto si realizza nella pratica perché se al sistema di spin
viene applicato ripetutamente e per tempi brevi un forte campo di
radiofrequenze (RF), si realizza una situazione in cui possono essere
eccitati simultaneamente i nuclei con frequenze di precessione di Larmor
ν i all’interno di un certo intervallo ∆ν . La ragioni di questo risiede nel
fatto che un tale campo di RF modulato da impulsi di frequenza ν o e breve
durata t p , produce bande laterali nell’intervallo ±1 t p separate tra loro da
una differenza di frequenza 1 tr dove t r è il tempo di ripetizioni dei singoli
impulsi.
Figura 4.14. (a) Sequenza di impulsi RF di frequenza vo, durata tp, tempo di
ripetizione tr; (b) Le corrispondenti frequenze componenti.
Questo è illustrato chiaramente in figura 4.14 dove il treno di
impulsi è mostrato su una scala dei tempi in figura 4.14a, e lo spettro di
frequenze di figure 4.14b.
In figura 4.14 b è illustrata la relazione tra ∆ν e numero di bande
laterali ed i parametri t p e t r . Si osservi che ∆ν diminuisce all’aumentare
di t p e, in condizioni limite, scompaiono le bande laterali.
101
NMR - Reologia
Riassumendo, l’impulso di radiofrequenza provoca una deflessione
del vettore M dall’asse z (direzione di Bo ) generando così la componente
Mxy , che a sua volta decade esponenzialmente con la costante di tempo T2 .
Quale risultato viene rilevato un voltaggio alternato in una spira
ricevitrice posta sull’asse x del sistema di laboratorio. Il segnale che viene
raccolto è detto free induction decay (FID).
Abbiamo già visto che l’angolo di deflessione θ è dato da:
θ = γB1t p
(4.65)
dove γB1 è la ampiezza o potenza dell’impulso RF e t p la sua durata
ed entrambi possono essere variati per ottenere gli angoli di deflessione
che interessano. Uno di questi può essere θ = 90° , per il quale tutta la
magnetizzazione è portata nel piano xy ed il segnale ha la sua massima
intensità (Figura 4.14.b). Un altro è θ = 180° ; in questo caso M è invertita
e punta nella direzione negativa dell’asse z (Figura 4.14.c).
4.3.6 Processo di Rilassamento
È
conveniente
rivedere
l’esperimento
NMR
pulsato.
Il
comportamento di Mo durante l’esperimento è descritto in figura 4.15.
Nell’esperimento è stato impiegato un impulso RF che ruota la
magnetizzazione di π 2 radianti (o 90°), cioè che la porta nel piano x' y '
(figura 4.15.c). M o è rappresentata in un sistema di coordinate che ruota
con B1 . A causa delle disomogeneità in Bo e nel campione (la seconda è
dovuta alle interazioni tra gli spin), i singoli dipoli nucleari non precedono
tutti alla stessa velocità ed i vettori tendono a sparpagliarsi nel piano
(figure 4.15.d e 4.15.e). le perdite di coerenza di fase risultante è
manifestata dal decadimento della componente Mxy che procede con la
costante di tempo T2 (si confrontino i paragrafi precedenti). Questo
processo di rilassamento non produce perdita di energia netta.
102
Capitolo 4
Contemporaneamente
si
osserva
che
anche
la
componente
longitudinale M z cresce, fino a raggiungere il valore di equilibrio M z , con
una legge cinetica di primo ordine caratterizzata da una costante di tempo
T1. (cfr figure 4.15.d, 4.15.e, 4.15.f):
dM z M o − M z
=
dt
T1
(4.66)
Questo processo è noto come rilassamento longitudinale o spinlattice.
Figura 4.15. Diagrammi nel sistemi di coordinate rotanti che mostrano
l'andamento della magnetizzazione durante l'esperimento NMR a impulsi. Gli assi
x', y', z' sono usati per indicare il sistema rotante. (a) La maagnetizzazione netta
Mo è allineata secondo il campo Bo; (b) e (c) E’ applicato un campo RF B1
perpendicolare a Bo. La durata dell’impulso di RF è sufficiente a far deflettere la
magnetizzazione di 90°; (d) e (e)Gli spin cominciano a rilassare nel piano x’y’ col
meccanismo spin-spin (con costante di tempo T2) e nella direzione z col
meccanismo spin-lattice (con costante di tempo T1); (f) La magnetizzazione di
equilibrio Mo si è ristabilita lungo Bo.
103
NMR - Reologia
4.3.7 Rilassamento trasversale o spin-spin
Procede con la costante di tempo T2 ed implica il trasferimento di
energia tra nuclei ad alta energia. Perciò questo tipo di rilassamento non
provoca perdita netta di energia, ma fa perdere coerenza di fase nel piano
xy, cioè è responsabile dell’azzeramento della componente M xy della
magnetizzazione che va a zero secondo la legge:
dM xy
dt
=−
M xy
(4.67)
T2
Il tempo di rilassamento T2 è correlato alla larghezza di riga a mezza
altezza dalla:
∆ν 0.5 =
1
πT2
(4.68)
4.3.8 Misura di T2
L’indagine NMR a basso campo per le misure dei tempi di
rilassamento di
1H
sono state condotte utilizzando l’apparecchiatura
Bruker Minispec mq20 NMR che opera ad una frequenza di 20 MHz (0.47
Tesla) e a diverse T (10°C- 25°C- 40°C).
La misura del tempo di rilassamento trasversale T2 è stata
determinata mediante la sequenza di impulsi Carr-Purcell-Meiboom-Gill
(CPMG): 90°-τ-{[180°-2τ-]M180°-τ-measurement-τ}N, dove τ è il tempo di
ritardo tra l’impulso a 90° e quello ad 180°. Il ritardo è di 5 sec. ed il
numero di scansioni 8.
Tale analisi prevede il riempimento per circa 2 cm di un tubetto di
vetro (diametro 8 mm) con il campione da studiare. Ad ogni misura, il
campo magnetico viene controllato ed il tempo di rilassamento misurato.
La temperatura è stata controllata con una precisione di ± 0.1°C mediante
il ricircolo di acqua distillata attorno al campione. La curva esponenziale
del tempo di rilassamento trasversale (T2) ottenuta, viene analizzata
104
Capitolo 4
mediante il fitting dei dati con una funzione multiesponenziale con un
programma informatico scritto in linguaggio FORTRAN.
4.3.9 Analisi del tempo di rilassamento T2
Il tempo di rilassamento trasversale T2 è stato studiato mediante il
fitting dei dati sperimentali da una funzione multi-esponenziale: fitting ai
minimi quadrati secondo l’algoritmo di Levenberg-Marquardt [9]:
Ne
∑ A e(
−t T2k
k
)
(4.69)
k =1
dove t è il tempo, Ak è il k-esimo fattore pre-esponenziale e T2k è il
k-esimo tempo di rilassamento. Il numero Ne di esponenziali considerati è
quello che minimizza il prodotto (Ne χ2) dove χ2 è la somma dei quadrati
delle differenze tra funzione eq. (4.69) che fitta i dati sperimentali ed i dati
sperimentali stessi.
Figura 4.16. Curva esponenziale del tempo di rilassamento trasversale T2
Una volta che Ne, A1, .., ANe, T21, .., T2Ne sono stati individuati
secondo la logica del miglior fitting, la distribuzione continua di T2 viene
determinata assumendo che per ogni istante di tempo t , il segnale
intensità I( t ) è la somma di infiniti termini del tipo a (T2 )e (−t T2 )dT2 . Pertanto
si ha:
105
NMR - Reologia
T2max
( ) ∫ a(T )e(
It =
−t T2 )
(4.70)
dT2
2
T2min
T2min - T2max indica il range di validità della distribuzione continua di
T2. L’integrale che compare nell’equazione (4.70) può essere approssimato
attraverso il metodo dei trapezi:
T2max
( ) ∫ a(T )e(
It =
∑ 0.5(a (T )e
i = N −1
−t T2 )
dT2 ≈
2
i
2
i
−t T2i
( )
i +1
+ ai+1 T2i+1 e −t T2
)(T
i +1
2
− T2i
)
(4.71)
i =1
T2min
dove T21 = T2min, e T2N = T2max. La semplificazione rappresentata in
eq. (4.71) implica approssimare la distribuzione continua di T2 con una
discreta composta da N elementi ognuno dei quali caratterizzato da un
peso
ai
corrispondente
ad
un
tempo
di
rilassamento
T2i.
La
determinazione dei pesi ai richiede la risoluzione di un sistema lineare di
N x N equazioni del tipo dell’ eq.(4.71), ognuna valutata a diversi istanti
di tempo t j . Pertanto, dopo alcune semplici manipolazioni, la generica
equazione di questo sistema diventa:
(
a1 e −t j
T21
(T
2
2
)) ∑ a (e
i = N −1
− T21 +
−t j T2i
i
(T
i +1
2
))
(
− T2i−1 +a N e −t j
T2N
(T
N
2
))
()
− T2N−1 = 2 I j t j
(4.72)
i=2
k = Ne
( ) ∑ A e(
dove I j t j =
−t j T2k
k
) . Siccome questo sistema è mal condizionato,
k =1
la risoluzione diretta generalmente fallisce. Di conseguenza, è necessario
risolverlo seguendo una procedura iterativa che implica la scelta di un
vettore di primo tentativo a(a1,..,ai,..aN). Scegliendo t j = T2i (per j = i), il
sistema assomiglia approssimativamente ad un sistema triangolare
superiore dove i valori dei coefficienti ai sotto la diagonale sono vicini allo
zero. Pertanto, una scelta ragionevole di primo tentativo per il vettore
(a0(a10,..,ai0,..aN0)) è:
a N0 =
2I N
;
T − T2N-1
N
2
m =i +1
2I i −
ai0 =
∑ a (T
0
m
m +1
2
)
− T2m−1 e −t i
m= N
T2i+1 − T2i−1
106
T2m
Capitolo 4
m =2
2 I1 −
a10 =
∑ a (T
0
m
m +1
2
)
m
− T2m−1 e −t1 T2
(4.73)
m= N
T22 − T21
Una volta che la scelta è stata fatta, la soluzione (an(a1n,..,ain,..aNn)
viene valutata nel seguente modo:
m = N −1
2I N −
a Nn =
∑
T2m
T2N − T2N −1
m ( ≠i )= N
∑
( )
amn −1e −t i
T2m
m ≠i =1
i +1
2
ain =
T
m= N
2 I1 −
a =
)
m =1
2I i −
n
1
(
amn −1 T2m+1 − T2m−1 e −t N
− T2i−1
∑a
n −1 −t N T2m
m
e
m =2
T22 − T21
(4.74)
Il processo iterativo si ferma quando il valore assoluto della
differenza ain − ain -1 è minore di una tolleranza fissata a priori. Questa è la
strategia che è stata adottata ed eseguita con l’uso di un programma
informatico scritto in linguaggio FORTRAN.
4.4 Caratterizzazione Reologica
Per la caratterizzazione reologica dei sistemi presi in esame lo
strumento utilizzato è il reometro rotazionale che lavora in configurazione
controlled stress, equipaggiata con sensori di diversa geometria in grado di
sottoporre il materiale ad una deformazione a taglio [7].
Essenziale per la caratterizzazione reologica è stabilire il legame tra
le grandezze dinamiche che caratterizzano lo stato di tensione del
materiale (lo sforzo tangenziale τ ) e le grandezze cinematiche che
rappresentano lo stato di flusso (la velocità di deformazione γ& ). Nelle
prove sperimentali si lavora con grandezze macroscopiche, applicando,
nello specifico, un momento torcente T (generato mediante un campo
magnetico) e registrando lo spostamento o la velocità di rotazione Ω della
parte mobile del sistema di misura, il cui valore dipende strettamente
107
NMR - Reologia
dalle proprietà del materiale inserito nel sistema di misura stesso (gli
attriti sono minimizzati da un sistema a cuscino d’aria). Da queste
grandezze macroscopiche deve essere possibile risalire ai valori puntuali
d’interesse, τ e γ& , in maniera relativamente semplice e per questo motivo i
dispositivi di misura devono avere un’adeguata geometria, di forma
semplice. La conversione tra le grandezze d’interesse è implementata nel
software di gestione dello strumento, grazie al quale è possibile accedere
ai dati che più interessano. È opportuno presentare brevemente alcuni
concetti riguardanti i sensori realmente utilizzati in fase operativa. In
sostanza si tratta di dispositivi costituiti da due piatti tra i quali viene
disposto il campione da esaminare in modo da ottenere un riempimento
ottimale del volume di misura.
4.4.1 Dispositivi di misura: Sistema a piatti paralleli
La geometria a piatti paralleli è largamente utilizzata per la misura
delle proprietà dei fluidi non newtoniani e per la caratterizzazione dei
materiali viscoelastici. Diverse sono le ragioni di tale largo uso: il
caricamento dei campioni è semplice, la shear rate può essere variata
indipendentemente
dalla
velocità
di
rotazione
W,
semplicemente
cambiando il gap d tra le superfici del sensore, lo slittamento alla parete
può essere stimato mediante prove a diversi gaps ed infine la edge failure
dei campioni può essere spostata a valori superiori di velocità di
deformazione diminuendo la distanza tra i piatti. Fonti di errore in fase
sperimentale possono essere lo strain field non omogeneo, come effetti
inerziali, sviluppo di flussi secondari e lo shear heating.
Occorre, tuttavia, tenere presente che anche le misure effettuate
con sistemi torsionali non sono esenti da circostanze ed effetti che
generano
errori
sistematici
in
fase
operativa;
alcune
situazioni
problematiche sono riassunte qui di seguito.
• Effetti inerziali: soprattutto ad alti valori di shear rate si
generano flussi secondari, di tipo toroidale, che fanno sovrastimare le
proprietà viscose dei materiali e, quindi, il momento torcente
108
Capitolo 4
misurato è maggiore del momento dovuto alle sole proprietà
reologiche.
• Effetti geometrici: se il fluido caricato è in eccesso, la
superficie libera non è sferica, e si generano effetti di bordo; altri
effetti possono derivare da un assetto non corretto, con conseguenti
eccentricità, mancanza di allineamento ed oscillazioni verticali.
• Effetti d’instabilità: il materiale non conserva la propria forma
in tutte le condizioni di moto ed alle alte velocità il campione tende a
separarsi in due lembi fino a giungere all’espulsione per effetto
centrifugo (splitting).
• Effetti del riscaldamento viscoso: se il sistema non è
termostatato in modo adeguato, all’interno del volume di misura si
raggiungono temperature superiori a quelle che si hanno alla
superficie e che sono oggetto di misura e controllo.
Figura 4.17. Rappresentazione schematica del sensore a piatti paralleli:
sono indicati il raggio dei piatti (R) ed il gap tra le due superfici (d).
4.4.2 Prove di stress sweep
L’utilità di un’indagine stress sweep, come già anticipato, risiede
nella possibilità di localizzare la regione di viscoelasticità lineare che
compete ai sistemi esaminati: in tale regione le componenti G’ e G” del
modulo elastico e viscoso si mantengono costanti, indipendentemente
dall’aumento della deformazione applicata, fino al raggiungimento di un
valore limite γ 0 , oltre il quale tali grandezze denotano una rapida
109
NMR - Reologia
diminuzione.
Le prove SS si basano sulla misura della risposta del campione
all’applicazione di uno sforzo variabile nel tempo secondo un profilo
sinusoidale d’ampiezza costante e frequenza oscillatoria fissata (1 Hz di
norma) in modo da poter individuare il valore della deformazione critica (o
dello sforzo critico) che delimita il campo di viscoelasticità lineare.
La risposta del sistema alla sollecitazione è anch’essa di tipo
sinusoidale, d’ampiezza proporzionale al carico applicato ma con un
ritardo di fase.
Per valori di sforzi (deformazioni) inferiori al limite di viscoelasticità
lineare i valori di G’ e G’’ sono indipendenti dallo sforzo applicato: le
condizioni del sistema possono essere considerate come stati d’equilibrio
in quanto la struttura del materiale non subisce significative alterazioni o
distruzioni.
Al superamento della deformazione critica, la struttura cede e i
valori d’entrambi i moduli cambiano, tendendo, di norma, a diminuire.
Le distribuzioni della deformazione, della velocità di deformazione e
degli sforzi possono essere descritte dalle seguenti equazioni:
γ = γ 0 sin (ωt )
(4.75)
γ& = γ 0 ω cos(ωt ) = γ& 0 cos(ωt )
(4.76)
τ = τ0 sin (ωt + δ ) = τ0 cos δ ⋅ sin (ωt ) + τ0 sin δ ⋅ cos(ωt )
(4.77)
dove γ0 è la deformazione massima, corrispondente al rapporto tra
lo spostamento massimo della piastra superiore e la distanza tra i due
•
piatti,
γ0
è la velocità di deformazione massima e ω la frequenza di
oscillazione.
Lo sforzo
τ
ha la stessa frequenza, ma è sfasato (di un angolo δ)
rispetto alla deformazione.
Il primo termine della formula:
τ = τ0 sin (ωt + δ ) = τ0 cos δ ⋅ sin (ωt ) + τ0 sin δ ⋅ cos(ωt )
110
(4.78)
Capitolo 4
rappresenta la componente elastica del comportamento reologico
del materiale, mentre il secondo è legato alla componente viscosa: nei due
casi limite, rappresentati da δ = 0 oppure da δ = π/2, si ha un
comportamento perfettamente elastico oppure perfettamente viscoso.
L’equazione (4.78) può essere riscritta come:
τ = G ' γ 0 ⋅ sin (ωt ) + G ' ' γ 0 ⋅ cos(ωt )
(4.79)
dove il modulo elastico G’ è legato alla componente in fase con la
deformazione applicata e il modulo dissipativo viscoso G’’ è in quadratura
di fase con essa. Questi moduli rappresentano il contributo elastico e
viscoso alle proprietà del fluido e sono legati alle corrispondenti funzioni
η’ e η’’ attraverso le:
G ' = η' ' ω
(4.80)
G ' ' = η' ω
(4.81)
Per un fluido newtoniano η’ coincide con la viscosità a taglio e G’ è
nullo, mentre per un fluido elastico è il modulo viscoso ad annullarsi.
Entrambe le coppie di variabili possono essere viste come la parte reale e
la parte immaginaria di una funzione complessa. Si possono scrivere sia
la viscosità complessa:
η* = η'−iη' '
(4.82)
che il modulo complesso:
G* = iωη* = G'+iG' '
(4.83)
Il modulo di G* è rappresentato dal rapporto tra il massimo sforzo e
la massima deformazione applicata:
2
G* =
(G ') + (G ' ')
2
2
Lo sfasamento δ è definito come:
tan δ =
G' ' η '
=
G' η ' '
2
τ cos δ τ0 sin δ
τ
+
= 0
= 0
γ0
γ0 γ0
(4.85)
111
(4.84)
NMR - Reologia
4.4.3 Prove di frequency sweep
Le prove di frequency-sweep permettono di ricavare lo spettro
meccanico del campione in esame e di conseguenza, di caratterizzare le
proprietà strutturali in condizioni d’equilibrio. Sulla base delle prove di
stress-sweep deve essere scelto un valore dello sforzo (strain) da applicare
durante le prove di frequency-sweep, tale da garantire la permanenza del
campione nel campo di viscoelasticità lineare (cioè G’ e G” indipendenti
dallo sforzo o deformazione applicata) per tutta la durata della prova. In
generale, la risposta di un materiale dipende sia dalle caratteristiche
strutturali intrinseche sia dall’entità della deformazione applicata e dal
tempo di applicazione della stessa. Un parametro da considerare per
classificare il comportamento di un materiale è il numero di Deborah che
corrisponde al rapporto tra il tempo caratteristico λ di rilassamento del
materiale e il tempo caratteristico del processo di deformazione cui il
materiale è sottoposto, Λ:
De = λ Λ ,
Λ ∝1 ω
De ∝ λω
I solidi reali possono esibire una componente viscosa subendo
deformazioni il cui recupero non è né completo né istantaneo. In molti
liquidi reali, quando lo sforzo viene rimosso, si ha in tempi osservabili, un
parziale
recupero
delle
deformazioni
e
quindi
si
manifesta
una
componente elastica. Quando il processo di deformazione è molto veloce,
De è molto grande: il materiale può comportarsi come solido elastico.
Invece quando il processo di deformazione è lento, De è piccolo, il
materiale può comportarsi come un liquido viscoso. Le prove condotte in
regime oscillatorio con deformazioni e sforzi di piccola ampiezza costante
consentono di sondare i differenti comportamenti di un materiale a
differenti numeri di Deborah.
4.4.4 Modelli di correlazione
Terminata la raccolta dei dati, è utile organizzare le informazioni in
maniera adeguata per facilitare l’interpretazione dei comportamenti
112
Capitolo 4
macroscopici osservati e per correlare i parametri compositivi ai parametri
reologici.
La caratterizzazione delle proprietà fisiche di questi idrogel, il grado
del rigonfiamento e la densità di reticolazione si possono valutare
attraverso
l’elaborazione
letteratura
propone
dei
diverse
dati
delle
soluzioni
proprietà
per
meccaniche.
l’approccio
alla
La
tempo-
dipendenza viscoelastica e per la conseguente caratterizzazione delle
relazioni G' (ω ) e G" (ω ) (spettri meccanici). Il punto di partenza è
rappresentato dalla combinazione dei sistemi che rappresentano gli
estremi tra i quali si colloca il comportamento dei materiali viscoelastici,
vale a dire il modello di fluido newtoniano, caratterizzato dalla viscosità µ
indipendente
dalle
condizioni
di
moto,
ed
il
modello
di
solido
perfettamente elastico, descritto dal modulo elastico G. Collegando in
serie queste due componenti, la deformazione sperimentata dall’apparato,
a fronte dell’applicazione di uno sforzo è data dai contributi viscoso
elastico
γ v ed
γe :
γ = γv +γe
(4.86)
Derivando rispetto al tempo e tenendo conto delle equazioni
costitutive che regolano le risposte dei componenti,
γ&v =
τ
µ
(4.87)
si ottiene:
τ+
µ ∂τ
G ∂t
= − µγ&
(4.88)
In tale espressione, che descrive il cosiddetto modello di Maxwell
(strain additive), il rapporto µ / G è a tutti gli effetti un tempo e viene
indicato come tempo caratteristico di rilassamento del sistema (λ) e,
qualora
il
modello
fisico
venga
utilizzato
per
approssimare
il
comportamento di sistemi reali, esprime il tempo necessario alla struttura
per rilassare gli sforzi in risposta all’applicazione di una deformazione
113
NMR - Reologia
costante. Significativo è il confronto di λ con i tempi caratteristici delle
varie prove, espressi nel caso dei test FS da 1/ω , operato mediante il
numero di Deborah (De) presentato in precedenza. Bassi valori di De
comportano un tempo di prova superiore al tempo di rilassamento del
materiale, il quale ha dunque a disposizione una finestra temporale
sufficientemente ampia per allentare lo stato di tensione e manifestare
una risposta prossima a quella viscosa. Al contrario, per valori elevati di
De il tempo di carico è talmente breve da non consentire al sistema di
riassestarsi: in tal modo il comportamento assume tratti tipici delle
risposte elastiche.
Applicando l’equazione al moto oscillatorio e lavorando con le
grandezze complesse, si ottiene:
G ′(ω ) =
η 0 λω 2
2
1 + (λω )
(4.89)
G ′′(ω ) =
η 0ω
2
1 + (λω )
(4.90)
Le curve di G’(ω) e G”(ω), che si possono tracciare in un grafico
bilogaritmico con queste relazioni, s’intersecano nel punto ω = 1 λ , in
corrispondenza di un massimo di G” e del valore unitario di De.
L’approccio
di
Maxwell
fin
qui
considerato
risulta
tuttavia
insufficiente nella descrizione delle risposte dei materiali analizzati in un
ampio range di condizioni: immaginando che i sistemi siano caratterizzati
dalla coesistenza di più modalità di rilassamento, si possono combinare
in parallelo n elementi di Maxwell, ciascuno individuato dalla coppia di
parametri (Gk ,η k ) o (Gk , λk ) , nell’intento di migliorare le prestazioni per il
trattamento dei dati. Il risultato è una configurazione del tipo stress
additive che in condizioni di moto oscillatorio restituisce le seguenti
relazioni:
η k λk ω 2
2
k =1 1 + (λ k ω )
n
G ′(ω ) = ∑
(4.91)
114
Capitolo 4
ηkω
.
2
k =1 1 + (λ k ω )
n
G ′′(ω ) = ∑
(4.92)
I parametri di fitting del modello di Maxwell generalizzato sono,
dunque, 2n:, i tempi di rilassamento λk e le viscosità η k (o, in alternativa,
i moduli elastici g k = η k λk ), ed è possibile aggiungere un termine residuo
G'e
che rappresenta il limite asintotico della componente elastica a basse
frequenze ed equivale ad un elemento di Maxwell nella condizione estrema
di pura elasticità, caratterizzata da un tempo di rilassamento infinito.
Un’ulteriore informazione che si ricava è lo spettro di rilassamento, ossia
la relazione g k (λk ) : essa permette di delineare l’entità con cui i diversi
componenti intervengono nelle modalità di rilassamento.
Nel caso specifico di questa trattazione, il numero di parametri
coinvolti nell’analisi numerica è stato ridotto, lasciando libero uno solo dei
tempi caratteristici λk e determinando i rimanenti mediante un fattore di
scala fissato a priori. In base alla finestra di frequenze sperimentalmente
accessibile, il numero di elementi con cui operare è stato fissato a quattro
o a cinque, lasciando il fattore moltiplicativo dei tempi pari a dieci.
Bibliografia
[1] Flory P J. Principles of Polymer Chemistry, Cornell University
Ithaca, NY, (1953).
[2] Schurz J, Progress in Polymer Science 16, (1991) 1-53.
[3] Brownstein KR, Tarr CE., Phys. Rev. A, 19 (1979) 2446-2452.
[4] P. J. Flory, Principles of Polymer Chemistry, Cornell University
Press, Ithaca, 1959.
[5] P. J. Flory, J. Chem. Phys. Principles of Polymer Chemistry,
Cornell University Press, Ithaca, 1959.
[6] P. J. Flory, N. Rabjohn, M. C. Shaffer, J. Polym. Sci., 4, 225,
435, 1949.
115
NMR - Reologia
[7] Lapasin R., Reologia: Appunti di Lezione, Dip. di Ing. Chimica,
Università degli Studi di Trieste, 2008.
[8] Alessandro Gambaro, Risonanza Magnetica Nucleare: Appunti
di Lezione, Stan's Library, Vol.II, 2008.
[9]
Numerical
Press,W.H.;
Recepies
Teukolsky,S.A.;
Vetterling,W.T.;
in
Cambridge
FORTRAN,
Cambridge, USA, 2nd edition, 1992.
116
Flannery,B.P.,
University
Press,