Spettroscopie per lo stato solido
L’ NMR allo stato solido
Teoria ed applicazioni
Piercarlo Mustarelli
Dipartimento di Chimica Fisica “M. Rolla”
Università di Pavia
SOMMARIO
1. Introduzione all'esperimento NMR: approccio classico e approccio quantistico
2. L’esperimento NMR
3. Meccanismi di rilassamento
4. Il ruolo della fase degli impulsi
5. La matematica dell’NMR: la trasformata di Fourier
6. Hamiltoniana di interazione e forma di riga
7. Tecniche per alta risoluzione nei solidi
8. La cross-polarizzazione (CP-MAS)
9. Informazioni ottenibili nei solidi
a. Sistemi a spin I=½
b. Sistemi a spin I>½
10. Attività di laboratorio
a. La strumentazione NMR per lo stato solido
b. Sintonizzazione della catena trasmittente-ricevente
c. Determinazione dell’impulso da 90° e sequenza di impulso singolo
d. Il ruolo delle fasi
e. Eco di Hahn
f. Misure di T1 e T2
g. Aggiustamento dell’angolo magico
h. Ricerca della condizione di Hartmann-Hahn
i. L’esperimento base CP-MAS
2
NMR - CENNI STORICI
~1936 Gorter e Broer studiano l'assorbimento di energia a radiofrequenza da parte di
nuclei di 7Li con tecniche calorimetriche. Non funziona perchè i materiali
usati sono troppo puri!!!
1945
Praticamente in contemporanea Bloch (Stanford) e Purcell (Harvard)
osservano il segnale dei protoni rispettivamente in acqua e paraffina (Nobel
condiviso nel 1952).
~ 1960 Primi esperimenti di Magic Angle Spinning (studio di solidi)
1966
Ernst e Anderson evidenziano la superiorità dell'NMR impulsato a
Trasformata di Fourier (FFT-NMR) sulla tecnica classica ad onda continua
(CW).
~1970 Sviluppo esplosivo delle applicazioni spettroscopiche, principalmente su 13C.
~1975 Sviluppo delle applicazioni di NMR allo stato solido in alta risoluzione.
~1990 Microscopia NMR allo stato solido. Misure MAS di routine. Applicazioni
multidimensionali allo stato solido (PASS, MQMAS)
3
1) INTRODUZIONE ALL'ESPERIMENTO NMR: APPROCCIO
CLASSICO E APPROCCIO QUANTISTICO
1a. LO SPIN NUCLEARE
Classicamente, un nucleo di massa mn e di raggio r che ruota con pulsazione ω ha un
momento angolare P (in modulo) dato da
P = ωmnr2 = 2π mnr2/tr
dove tr è il tempo di rotazione. Al momento angolare corrisponde un momento
magnetico
µ=
qP
2 mn
Il termine q/2mn si indica con γ e prende il nome di rapporto giromagnetico. Al
momento angolare viene associata la grandezza quantistica spin nucleare, I, dato da:
µ=
P = hI
qhI
= γhI
2 mn
I valori assunti dallo spin nucleare sono funzione del numero di neutroni e di protoni
che formano il nucleo:
Numero atomico
Pari
Pari
Dispari
Dispari
Peso atomico
Numero quantico, I
Esempi
0
n/2
n
n/2
12C,16O,
Pari
Dispari
Pari
Dispari
…
13C,17O, 29Si,
…
…
1H, 7Li, 15N, …
2H, 6Li, 14N,
Le grandezze dei momenti magnetici vengono normalmente espresse in termini del
rapporto giromagnetico γ espresso in megahertz/tesla; ad esempio, per il nucleo 1H si
ha γ = 42.577 MHz T−1. In altre parole, i protoni che si trovano immersi in un campo
magnetico di 1 tesla risuonano a 42.577 MHz (vedi pagina seguente).
4
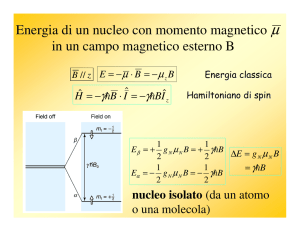
1b. IL NUCLEO IMMERSO IN UN CAMPO MAGNETICO
Un nucleo a spin nucleare I ≥ ½ immerso in un campo magnetico B0 acquista una
energia data da
E = −µ•B0 = −µB0cos θ = −µzB0
e precede attorno alla direzione del campo magnetico come mostrato in figura.
La precessione attorno a Bo prende il nome di precessione di Larmor ed è
l'equivalente elettromagnetico della precessione di una trottola nel campo
gravitazionale. Le leggi della dinamica classica affermano che la variazione nel
tempo del momento angolare è uguale al momento torcente dato dall'interazione tra µ
e Bo
dI
= µ × Bo = Iω o
dt
da cui riarrangiando si ottiene la prima equazione fondamentale dell'NMR,
l'equazione di Larmor
ω = γBo
che collega la frequenza di precessione all’intensità del campo magnetico
sperimentato dal nucleo in oggetto.
5
1c. IL VETTORE MAGNETIZZAZIONE MACROSCOPICA
Data una popolazione di nuclei all’equilibrio immersa in un campo magnetico,
per le singole componenti lungo gli assi cartesiani valgono le seguenti relazioni:
∑ µx = ∑ µ y = 0
i
i
∑ µz = M z
i
per cui il momento magnetico totale può essere rappresentato con un vettore M di
componente Mz.
Dal punto di vista quantistico, l’esistenza di una campo magnetico esterno B0
causa la rimozione della degenerazione dei livelli energetici. Nel caso semplice I = ½,
si ottengono due livelli corrispondenti agli autovalori –½ e ½
1
E1 / 2 = − hγB0
2
E −1 / 2 =
B0 = 0
1
hγB0
2
B0 ≠ 0
All’equilibrio, la popolazione dei livelli energetici è fornita dalla statistica di
Boltzmann
∆E
−
µB
n1
= e kT ≅ 1 + 0
n2
kT
da cui risulta che lo stato fondamentale è più popolato. A temperatura ambiente
(kT ≅ 0.025 eV) la differenza è dell’ordine di 10-5 (bassa sensibilità dell’NMR).
6
1d. L'ECCITAZIONE A RADIOFREQUENZA
L'eccitazione del sistema di spin viene realizzata applicando un campo a
radiofrequenza definito come
B1(t) = B1 cos ω1t
Quando la frequenza angolare di rotazione di B1 eguaglia quella di Larmor del nucleo
si ha la condizione di risonanza: il sistema di spin assorbe energia dal campo a
radiofrequenza e la magnetizzazione netta ruota verso il piano convenzionalmente
chiamato x-y
A. Approccio classico
In pratica, l'eccitazione viene applicata con un campo polarizzato linearmente lungo x
o y. Un campo di questo tipo può essere risolto in due componenti controrotanti, della
quali una ruoterà attorno all'asse z nella corretta direzione, mentre l'altra non avrà
effetto alcuno.
7
Il sistema di riferimento rotante
Considerando un sistema di coordinate rotanti x’, y’, z’ con pulsazione ω1, il moto del
vettore magnetizzazione macroscopica M è dato da:
dM
= γM × Beff
dt
dove il campo Beff è dato da
Beff = ( B0 −
ω rf
)k + B1i
γ
Per ωrf = ω0 il vettore M precede attorno a B1. L’angolo di rotazione, θ, in funzione
della lunghezza dell’impulso a radiofrequenza τ, è dato da
θ = γ B 1τ
z’
y’
B1
x’
8
B. Approccio quantistico
Dato un sistema a più livelli (I ≠ 0), il campo a radiofrequenza determina transizioni
tra i livelli stessi.Nel caso semplice I = ½ si ha:
1
E1 / 2 = − hγB0
2
∆E = hγB0
E −1 / 2 =
1
hγB0
2
e lo spettro NMR consiste di una sola riga a frequenza ∆E = hγB0 , mentre nel caso di
spin I>1/2 lo spettro consiste di 2I righe, corrispondenti alle transizioni tra i (2I+1)
livelli energetici.
9
2) L’ESPERIMENTO NMR
In generale, un esperimento NMR consiste di tre fasi:
1) la preparazione del sistema di spin
2) l’evoluzione del sistema di spin
3) la rivelazione del segnale nucleare
preparazione
evoluzione
rivelazione
Il più semplice esperimento possibile consiste nella applicazione di un impulso RF di
90°
90o
Canale trasmittente
2 D
G r a p h
1
2
Free Induction Decay, FID
Y Data
1
Canale ricevente
0
-1
0
1 0
2 0
3 0
X
D
4 0
5 0
6 0
7 0
t
10