1
Tutorato Lezione 2 Gli amplificatori operazionali
Ideale:
Gli op-amp sono circuiti elettronici di base ideati e sviluppati con la nascita delle prime macchine di
calcolo analogico. In seguito con l’avvento dell’elettronica digitale il loro utilizzo rimase comunque
incentrato sull’elaborazione di segnali analogici, In quanto tramite questi circuiti è possibile
comunque svolgere un’elevato numero di operazioni tra di essi, come amplificazione di somme
differenze, realizzazione di circuiti integratori, derivatori, somme di segnali etc….
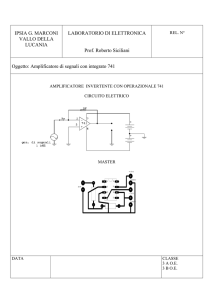
Lo schema base con cui possiamo rappresentare un amplificatore operazionale è ancora quello del
generatore controllato che amplifica la differenza di due segnali in ingresso.
−
out
v1
+
±
A(v2 − v1 )
v2
Per un op-amp si definiscono:
Il segnale di ingresso differenziale come la differenza dei segnali che sono presenti ai terminali
v ID = (v 2 − v1 )
E il segnale di modo comune come la media dei segnali presenti ai due terminali
v ICM =
1
(v1 + v2 )
2
Idealmente un op-amp ha una resistenza di uscita nulla e una resistenza di ingresso infinita.
Molte delle potenzialità e delle operazioni che vengono realizzate con gli amplificatori operazionali
derivano dal fatto che possono essere utilizzati come circuiti reazionati con una reazione negativa.
Come insegna la teoria dei controlli un blocco reazionato può essere schematizzato come in figura
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
2
xs
+
−
xi
Σ
A(s )
xO
xf
β (s )
Possiamo scrivere le equazioni del sistema come segue:
xO segnale in uscita dal sistema
xi segnale in ingresso alla catena dei sistemi
xs segnale che proviene dal generatore
Σ circuito sommatore
A= guadagno ad anello aperto del sistema
β = tasso o fattore di controreazione
Possiamo scrivere le seguenti equazioni
xO = Axi
x f = β xO = Aβxi
x s = xi + x f ⇒
xO
+ β xO
A
x
1 + Aβ
A
⎛1
⎞
)⇒ O =(
)
x s = xO ⎜ + β ⎟ = x O (
A
xs
1 + Aβ
⎝A
⎠
Dove Aβ viene definito come guadagno d’anello del sistema
Le cose cambiano un po nel caso dell’amplificatore operazionale in quanto abbiamo due terminali
di ingresso
Per esempio consideriamo la retroazione sul terminale negativo quando il terminale positivo è a
massa
x
1 + Aβ
A
⎛1
⎞
)⇒ O =(
)
x s = xO ⎜ + β ⎟ = xO (
A
xs
1 + Aβ
⎝A
⎠
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
3
Per il momento non eseguiamo il calcolo del guadagno d’anello e del guadagno a ciclo chiuso del
sistema utilizzando la teoria della retroazione, che riprenderemo quando a lezione vedrete i quattro
tipi di controreazione ma studiamo le due configurazioni fondamentali dell’operazionale reazionato
con elementi passivi utilizzando solo i concetti di corrente e tensione del sistema.
Consideriamo invece il calcolo utilizzando il bilanciamento delle correnti e tensioni andando ad
esaminare entrambe le configurazioni partendo dalle idealità ed eliminando le idealita
La configurazione invertente
L’operazionale idealmente parlando è un amplificatore caratterizzato dall’avere un guadagno
infinito.
v−
−
vid
A
+
−
+
vO
v+
Se considerato così la relazione tra ingresso uscita sarà:
v0
v
= A → vid = O
vid
A
Ora se
v
A → ∞ ⇒ O → 0 ⇒ vid = 0 ; ⇒ v + = v −
A
siccome la tensione presente sul nodo positivo è nulla allora la tensione sul nodo negativo è nulla e
stiamo facendo l’ipotesi di cortocircuito virtuale
Cioè avere un guadagno infinito equivale ad annullare la tensione differenziale che si ha in ingresso,
ma è una conseguenza!! Non vuol dire che il sistema non funziona, infatti se passiamo al sistema
reazionato per esempio da elementi passivi abbiamo che possiamo scrivere le equazioni di
kirkchoff:
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
4
v2
R2
i2
v1
R1
vS
i1
+
i−
v−
−
vid
−
+
v+
vO
Dobbiamo trovare la legge che lega la tensione di uscita alla tensione di ingresso
Siccome l’amplificatore è ideale ha una resistenza di ingresso infinita una resistenza di uscita nulla
e un guadagno a ciclo aperto infinito
La tensione sull’uscita viene riportata indietro da una rete di reazione composta da elementi passivi
Possiamo scrivere l’equazione al nodo di ingresso per le correnti
Per la legge di kirckoff la somma delle correnti entranti nel nodo deve essere uguale alla somma
delle correnti uscenti
i1 = i− + i2
Avendo l’operazionale una resistenza ideale di ingresso idealmente infinita la corrente che entrerà
nel terminale invertente dell’amplificatore è nulla
i1 = i2
Poi possiamo scrivere anche l’equazione alla maglia considerando le tensioni
v s = v0 + v1 + v 2 ⇒ v s − v0 − v1 − v 2 = 0
O scritta in termini di correnti
v s − v 0 − i1 R1 − i2 R2 = 0 ⇒ v s − v0 − i1 R1 − i1 R2 = 0
La corrente
i1 =
vs − v−
R1
La v- abbiamo detto che è nulla per il cortocircuito virtuale quindi
i1 =
vs
R1
Inserendo questa nell’equazione trovata in precedenza si ottiene
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
5
v s − v0 −
vs
v
v
R1 − s R2 = 0 ⇒ −v0 − s R2 = 0
R1
R1
R1
v 0 − R2
=
vs
R1
La resistenza di ingresso è quella che si vede guardando da dove viene applicato il generatore di
ingresso applicando un generatore di prova vx e misurando la corrente ix
R2
RIN
R1
vx
ix
−
+
−
+
Per la presenza del cortocircuito virtuale si vede solo la R1 connessa a massa
La resistenza di uscita si calcola allo stesso modo ma considerando un generatore di prova di
corrente applicato in uscita.
R2
ROut
R1
−
+
+
v+
vx
−
ix
v x = i1 R1 + i2 R2
i1 = i2
Siccome la R1 p tra massa e massa non ci può essere corrente che la attraversa vista dall’uscita
quindi anche I2=0 allora
ROut = 0
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
6
Togliendo le on idealità si ottengono e ripetendo i ragionamenti e reinterpretando i risultati con la
teoria dei controlli si ottengono le seguenti espressioni
Av0
β
RIN
ROut
guadagno dell’amplificatore apertoin continua
fattore di reazione
resistenza di ingresso
resistenza di uscita
Av 0 =
β=
− R2
R1
⎛ A0 β
⎜⎜
⎝ 1 + A0 β
⎞ − R2
⎟⎟ ≈
;
R1
⎠
R1
1
=
1 + Av0
R1 + R2
⎛
R2
RIN = R1 + ⎜⎜ RID //
1 + A0
⎝
⎞
⎟⎟ ≈ R1 ;
⎠
ROUT =
RO
1 + A0 β
invece è il fattore di retroazione
I limiti sulla R2
Dato che la RID dell’amplificatore ha un valore finito nel morsetto invertente entra comunque una
corrente. Affinché il sistema funzioni però la corrente che entra deve essere minore della corrente
che scorre in R2 in pratica deve essere trascurabile rispetto ad essa.
Come indicazione pratica di progetto si assume che il valore limite della resistenza R2
R
R2 (max ) = ID
2
Ora come già detto il guadagno di un’amplificatore è funzione della frequenza e il suo andamento
sarà rappresentato dal diagramma di Bode, per ora ci interessa solo il modulo e si l’ipotesi di
singolo polo
AdB
A0
0
ωB
ωT
ω = 2πf
Per effetto
della reazione
La risposta dell'amp ad anello chiuso
viene modificata ovvero è possibile diminuire il guadagno
rispetto a quello che avrebbe il sistema a ciclo aperto e
aumentare la banda passante del sistema
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
7
A0ω B
ωT
=
dove
G BW = ωT = A0ω B gain badwidth è il prodotto guadagno
s + ωB s + ωB
larghezza di banda che per definizione è la frequenza a guadagno unitario, ovvero la frequenza a cui
il guadagno si riduce a 1=0dB.
A(s ) =
AV = −
R2 A(s )β
;
R1 1 + A(s )β
ora sostituendo As nell’espressione calcolata sopra si ottiene
⎛ R2 ⎞ A0 β
A0ω B
⎜⎜ −
⎟⎟
β
R
⎛ R2 ⎞ s + ω B
1 ⎠ (1 + A0 β )
⎟⎟
=⎝
AV = ⎜⎜ −
s
⎝ R1 ⎠ 1 + A0ω B β
+1
ω B (1 + A0 β )
s + ωB
Che per
A0 β >> 1
Diventa
⎛ R2 ⎞
A0ω B
⎜⎜ −
⎟⎟
β
R
⎛ R2 ⎞ s + ω B
1 ⎠
⎟⎟
=⎝
AV = ⎜⎜ −
s
ω
A
R
1 ⎠
⎝
+1
1+ 0 B β
ωH
s + ωB
Dove
ωH =
ωt
≈ βω T
A0
(1 + A0 β )
Cosa succede dal punto di vista della risposta in frequenza quando si mettono più stadi in cascata?
AV (s ) =
AV 1 (0)
⎛
s ⎞
⎟⎟
⎜⎜1 +
ω
H1 ⎠
⎝
⋅
AV 2 (0)
⎛
s
⎜⎜1 +
⎝ ωH 2
⎞
⎟⎟
⎠
⋅⋅⋅
AVN (0)
⎛
s
⎜⎜1 +
⎝ ω HN
⎞
⎟⎟
⎠
La larghezza di banda dell’amplificatore rappresenta la frequenza alla quale il guadagno di tensione
si riduce del fattore
1
− 3dB =
2
Se si mettono nel caso particolare N amplificatori in cascata identici si ottiene:
⎡
⎤
⎢ A (0 ) ⎥
⎥
AV (s ) = ⎢ V 1
⎢1 + s ⎥
⎢ ωH1 ⎥
⎣
⎦
N
Si trova che la banda passante si riduce di un fattore che dipende da quanti stadi metto in cascata:
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
8
f H = f H 1 = 21 / N − 1
Dove N è il numero degli stadi.
Quindi possiamo riportare in una tabellina i risultati finora trovati e ripetere il ragionamento per la
configurazione non invertente
Si HA
CONFIGURAZIONE INVERTENTE
Av 0 =
β=
R
− R2
; R IN = R1 ; ROUT = O dove RO è la resistenza di uscita propria dell’amplificatore
R1
A0 β
R1
1
; f H1 =
=
R1 + R2 1 + AV (0)
fT
; f H = f H 1 21 / N − 1
A0
1 + A0 β
CONFIGURAZIONE NON INVERTENTE
Av 0 = 1 +
R2
;
R1
R IN = RID (1 + A0 β ) ; ROUT =
RO
R1
1
=
; β=
;
A0 β
R1 + R2 1 + AV (0)
f H1 =
fT
;
A0
1 + A0 β
f H = f H 1 21 / N − 1
La differenze fondamentali tra i due stadi stanno nel fatto che:
La configurazione invertente fornisce in uscita uno sfasamento di 180° del segnale di ingresso
La configurazione non invertente ha a parità di guadagno una banda più ampia rispetto a quella
invertente dovuto al fatto che l’espressione del guadagno è 1+….
AV (inv) = −
R2
,
R1
ω 3dB =
ωt
1 + R2 R1
AV (noninv ) = 1 +
R2
R1
ω 3dB =
ωt
1 + R2 R1
A parità di guadagno quindi la configurazione non invertente permette di avere una ω 3dB maggiore
rispetto alla invertente perché si ottiene lo stesso valore del guadagno con valori di resistenza più
piccoli.
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
9
Esercizio 1
Progettare un amplificatore di tensione per un canale telefonico in grado di fornire un guadagno di
tensione pari a Av = 90dB nella banda passante a 3dB 100 Hz ÷ 4.5 KHz con impedenza di ingresso
RIN ≥ 68KΩ e impedenza di uscita ROUT = 4.7 KΩ
Si dispone di condensatori con tolleranze del 10% , di resistori con tolleranze del 5% e di
amplificatori operazionali con le seguenti caratteristiche:
Av = 106dB
CMRR = 80dB
R ID = 2 MΩ
VOS < 5mV
VO (max ) = ±12V con RL > 2 KΩ
SR = 0.5V µ sec
RO = 75Ω
I B < 500nA
GBW = 1MHz
I OS < 500nA
Traccia di una possibile soluzione
Ci viene chiesto di realizzare un circuito con la risposta in frequenza rappresentata in figura 1
utilizzando degli amplificatori operazionali con la risposta in frequenza rappresentata in figura 2
Figura 1
Figura 2
La prima cosa da calcolare è quanti stadi serviranno. Chiudendo l’amplificatore con una retroazione
che può essere sia negativa che positiva ci muoviamo infatti dentro la figura 2 tenendo presente che
a una riduzione del guadagno corrisponde un aumento della banda.
Per calcolare il numero degli stadi necessari dobbiamo prima sapere qual’è il massimo guadagno
ottenibile con uno stadio e questo viene fissato dal rapporto tra le due frequenze di taglio ad anello
aperto e chiuso
1 ⋅ 10 6
A(max) =
= 222.23 → 46.9dB
4.5 ⋅ 10 3
Ovviamente per arrivare a 90 dB ≈ 31623 mi serviranno almeno due stadi!!.
Se decido di usare due stadi la cosa più semplice da fare è vedere se posso ottenere le specifiche
utilizzando due stadi uguali.
Per fare questo devo considerare il limite imposto dalla frequenza superiore e il fattore di riduzione
della banda passante dovuto all’utilizzo di più stadi uguali in cascata.
Indicando quindi con f H 1 e f H 2 le frequenze di taglio superiori, rispettivamente del primo e del
secondo stadio abbiamo la seguente relazione:
⎛ f H1 + f H 2 ⎞
⎜
⎟ ⋅ 0.644 = 4.5 KHz
2
⎝
⎠
Da cui se imponiamo f H 1 = f H 2 = f H essendo gli stadi uguali otteniamo
4.5 KHz
≈ 6.99 KHz
0.644
Questo ci dice che la frequenza di taglio superiore per il singolo stadio sarà di 6.99 KHz .
Possiamo ora calcolare il guadagno corrispondente dividendo GBW del 741 per f H
fH =
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
10
A(max ) =
1 ⋅ 10 6
= 143 → 43dB
6.99 ⋅ 10 3
Per arrivare al guadagno richiesto occorre aggiungere uno stadio con un guadagno di 4dB ≈ 1.58 .
Essendo il guadagno piccolo, il polo è a una frequenza molto alta rispetto a quella richiesta dalle
specifiche e quindi non le influenza.
fH =
1 ⋅ 10 6
= 446.428 KHz che risulta molto maggiore di 4.5 KHz
2.24
Possiamo quindi disegnare un primo schema a blocchi.
Nella figura c’è un’errore il guadagno del terzo stadio è 4 non 7dB.
Adesso dobbiamo vedere come possiamo realizzare le configurazioni richieste e questo possiamo
farlo applicando le formule
Dalla teoria sappiamo che possiamo utilizzare l’amplificatore sia in configurazione invertente che in
configurazione non invertente.
Abbiamo una specifica sulla resistenza di ingresso del sistema che deve essere di 68KΩ e una sulla
resistenza di uscita.
Sicuramente la resistenza di uscita per entrambe le configurazioni è
RO
con A0β>>1
A0 β
La resistenza di uscita è piccola pertanto per ottenere la Rout richiesta si metterà un carico di
4.7KΩ in serie.
ROUT =
Per la resistenza di ingresso possiamo esaminare entrambe le configurazioni e fare un’analisi
comparata per vedere quale sarà la migliore.
Se scegliamo di utilizzare la configurazione invertente avremo che
Per soddisfare la specifica sulla resistenza di ingresso dovremo scegliere una resistenza di ingresso
R1 almeno pari al valore indicato.
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
11
RIN = R1 = 68KΩ
Mentre per il fatto che il guadagno dell’amplificatore deve essere di 43dB=141.25 dovremo
utilizzare una
R2 = 141.2 R1 = 141.2 ⋅ 68 KΩ = 9.6 MΩ
Ma in questo caso dato che questo valore di resistenza è più grande di quello della RID la corrente
che scorrerebbe su di essa è minore di quella su RID mentre dovrebbe succedere l’esatto contrario
infatti si ha come regola pratica
R2 (max ) =
R ID
≈ 1MΩ
2
Che anche commercialmente è un valore limite.
Se vogliamo utilizzare la configurazione invertente come primo stadio dobbiamo quindi ricorrere ad
uno schema circuitale differente caratterizzato dal fatto di offrire un’alta impedenza e quindi
utilizzare l’operazionale ad alta impedenza!
La cui espressione del guadagno è data dalla relazione:
A=−
R2
R1
⎛
R
R ⎞
R
⎜⎜1 + 4 + 4 ⎟⎟ da cui imponendo : 2 = 10 → R2 = 680 KΩ e R4 = R2 il valore di
R 2 R3 ⎠
R1
⎝
R3 = 55.28ΩK ≈ 56 KΩ considerando i valori delle resistenze al 5%.
I seguenti valori di resistenza permettono di ottenere il guadagno pari a
680 ⎞
⎛
A = −10⎜1 + 1 +
⎟ = 141.43 .
56 ⎠
⎝
Mettendo insieme questi stadi considerando il fattore di riduzione della banda passante e del
guadagno si ottiene un’amplificazione con guadagno
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
12
A = 141.43 ⋅ 141.3 = 86 dB
Essendo la
fH =
10 MHz
≈ 7 KHz
141.3
Dobbiamo ora realizzare il circuito non invertente del sistema
⎛
R ⎞
4dB = ⎜⎜1 + 2 ⎟⎟ si sceglie un valore con tolleranza del 5% e si calcola il corrispondente valore di
R1 ⎠
⎝
R2
R1=10KΩ R2=15.8KΩ.=16ΚΩ
Rimane ora da fissare la frequenza di taglio inferiore del circuito in modo che vengano tagliate le
frequenza al di sotto dei 100 Hz . Per fare questo possiamo aggiungere in serie alla resistenza di
ingresso di uno stadio un condensatore il cui valore si ottiene facilmente dalla relazione:
C=
1
≈ 24nF
2πfR
Il condensatore ha anche la funzione di bloccare le componenti in continua del primo stadio che se
troppo elevate comprometterebbero il corretto funzionamento del secondo stadio.
Per quanto riguarda invece l’ultimo stadio possiamo scegliere
pertanto una prima possibile soluzione del circuito è la seguente
680K
680K
16 K
680K
680K
56K
68K
56K
−
+
68K
10 K
−
−
+
24n
+
Ovviamente non è necessario realizzare il secondo stadio con una configurazione invertente ad alta
impedenza in quanto on si hanno vincoli sulla resistenza di ingresso, pertanto dato che la resistenza
di uscita del primo amplificatore è molto bassa, possiamo realizzare un secondo stadio con una
configurazione invertente semplice!!
Se invece come primo stadio decidessimo di utilizzare una configurazione noninvertente avremo:
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
13
R IN = RID (1 + A0 β ) la specifica sulla resistenza di ingresso sarà soddisfatta a prescindere dai valori
di resistenze che si utilizzeranno perché la resistenza di ingresso è molto elevata e per default va
pure meglio infatti sappiamo che per un amplificatore di tensione la resistenza di ingresso deve
essere la più elevata possibile.
Possiamo fissare la banda per uno stadio che sarà pari a 7KHz e andare a determinare qual è il
guadagno ottenibile.
f 3dB =
⎛
ft
R ⎞ 1 ⋅ 10 6
⇒ ⎜⎜1 + 2 ⎟⎟ =
= 143
R1 ⎠ 7 ⋅ 10 3
1 + R2 R1
⎝
⎛
R ⎞
R
⎜⎜1 + 2 ⎟⎟ = 143 ⇒ 2 = 142
R1 ⎠
R1
⎝
In aggiunta a questo possiamo scegliere il valore di resistenza che preferiamo senza inficiare il
valore della resistenza di ingresso del progetto e rispettando il limite pratico per il valore della
corrente che deve scorrere sulla R2 infatti ricordiamo che
R2 (max ) =
R ID
≈ 1MΩ
2
Scegliendo un valore sulla tabella dei componenti standard per R si vede che non possiamo
soddisfare tale specifica con i valori standard, pertanto dovremo scegliere una combinazione di
resistori esistenti sul mercato che mi dia il guadagno un po inferiore e una banda un po maggiore
R1=820KΩ
R2=6.2KΩ
R2 820
=
= 132.26
R1 6.2
fH
1 ⋅ 10 6
=
= 7.56 KHz
132.26
Per cui avremo mettendo due stadi in cascata identici
f HT = 7.56 KHz ⋅ 0.644 ≈ 4.87 KHz
Che soddisfa la specifica sulla banda
Ora il valore del guadagno ottenuto espresso in decibel è:
AdB = 20 log(132.26) = 42.42dB
Per cui mettendo insieme due stadi in cascata si ottiene
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
14
A = A1 + A2 = 84.8dB
Servirà mettere un terzo stadio che abbia un guadagno di
A3 = 2
Allora avremo
⎛
R ⎞
R
⎜⎜1 + 2 ⎟⎟ = 2 ⇒ 2 = 1
R1 ⎠
R1
⎝
Basta scegliere due valori che sono presenti sul mercato e metterli per es: 10KΩ
In questo caso la banda il polo che introdurrà il terzo amplificatore sarà a 500MHz e non influenza
il comportamento del sistema alla frequenza che vogliamo noi.
Quindi una possibile configurazione è:
10K
820K
820K
10K
−
6.2K
6.2K
−
+
−
C
+
+
+
−
Rimane da mettere la resistenza in uscita che si aggiunge semplicemente inserie
E fare in modo che la banda del sistema tagli le frequenze sotto i 100Hz
Si procede come nel caso precedente tenendo presente che qui la
⎛
⎛ 10 KΩ ⎞ ⎞
11
R IN = RID (1 + A0 β ) ⇒ 2 ⋅ 10 6 ⎜⎜1 + 1.99 ⋅ 10 5 ⎜
⎟ ⎟⎟ = 1.99 ⋅ 10 Ω
20
K
Ω
⎝
⎠⎠
⎝
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
15
Per cui basta un capacitore di:
C=
1
1
=
= 8 fF
2πfR 2π 100 ⋅ 1.9911
Troppo piccolo!! Deve essere almeno delle centinaia di pF
Pertanto posso metterlo tra il primo e il secondo stadio?
⎛
⎛ 6.2 KΩ ⎞ ⎞
9
R IN = RID (1 + A0 β ) ⇒ 2 ⋅ 10 6 ⎜⎜1 + 1.99 ⋅ 10 5 ⎜
⎟ ⎟⎟ = 2.98 ⋅ 10 Ω
826
.
2
K
Ω
⎝
⎠⎠
⎝
C=
1
1
=
= 534 fF
2πfR 2π 100 ⋅ 2.98 9
Se posso realizzarlo ok se no torno indietro per esempio imponendo un valore di 500fF che posso
realizzare connettendo in serie due capacitori da 1pF e calcolo il valore della RIN
Es
R=
1
1
=
= 3.18 9 Ω
−15
2πfC 2π 100 ⋅ 500
Calcolo il beta
3.18 9 = RID (1 + A0 β ) ⇒ β = 0.080
⎛
R ⎞
1
⎜⎜1 + 2 ⎟⎟ =
= 125 = 41.93dB
R1 ⎠ 0.0080
⎝
La ft di due stadi messi in cascata sarà quindi
10 6
0.644 ≈ 5.125KHz che soddisfa la specifica sulla banda ma ci sono 500KHz in più…
125
Se danno fastidio non si può seguire questa strada e la soluzione più semplice è utilizzare una
configurazione invertente come ultimo stadio per poter trovare un valore di capacità realizzabile.
Oppure provare con stadi diversi; per esempio si potrebbe provare a realizzare uno stadio con
specifica sulla banda 4.5KHz avente guadagno di:
10 6
= 67 dB
4.5 3
E un secondo stadio di guadagno di
Tutorato Lez.2 Glia amplificatori operazionali [email protected]
16
23dB = 14.1 ⇒
16
≈ 71KHz
14.1
Vedendo se è possibile soddisfare le specifiche.
Come possiamo vedere ci sono molte soluzioni, per un esame vi conviene abbozzare la soluzione
più semplice quella per cui ci mettete meno tempo, poi motivare se va bene o meno e cambiarla
Tutorato Lez.2 Glia amplificatori operazionali [email protected]