Matematica e Statistica
Modulo di Matematica
Sonia L’Innocente
Corso di Laurea
Biologia della Nutrizione
Argomento 4.
Derivate
a.a.
2013-2014
Sonia L’Innocente
Sonia L’Innocente (Camerino)
1 / 26
Derivate
Outline
1
Derivate
Significato geometrico della derivata di una funzione
Teoremi legati alla derivata
Derivate di ordine superiore
Uso delle derivate per il calcolo dei limiti
Sonia L’Innocente
Sonia L’Innocente (Camerino)
2 / 26
Derivate
Iniziamo con l’osservare che se t è una variabile che rappresenta il
tempo e se p(t) è una funzione che rappresenta il peso di un
determinato corpo al tempo t, allora nell’intervallo di tempo [t, t + h],
con h > 0, il peso del corpo varia da p(t) a p(t + h) ed il rapporto
p(t + h) − p(t)
h
indica di quanto è variato in media il peso nell’unità di tempo, tale
rapporto è detto tasso medio di accrescimento o tasso medio di
variazione o velocità media di variazione.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
3 / 26
Derivate
Se, invece della variazione media, si vuole la variazione istantanea
allora si deve considerare
p(t + h) − p(t)
h
h→0
lim
il quale è detto tasso di accrescimento.
Se invece t è una variabile che rappresenta il tempo e s(t) è una
funzione che rappresenta lo spazio percorso da un corpo al tempo t,
allora la quantità
s(t + h) − s(t)
h
rappresenta la velocità media tenuta dal corpo nell’intervallo di
tempo [t, t + h], mentre la quantità
s(t + h) − s(t)
h
h→0
lim
rappresenta la velocità istantanea tenuta dal corpo al tempo t.
Sonia L’Innocente (Camerino)
Sonia L’Innocente
4 / 26
Derivate
Derivata
Definizione. Data una funzione f : (a, b) → R e dato x ∈ (a, b), si
definisce rapporto incrementale in x la seguente quantità
f (x + h) − f (x)
,
h
h ∈ R, h 6= 0
e si dice che f è derivabile nel punto x se esiste ed è finito il
seguente limite
f (x + h) − f (x)
lim
,
h
h→0
il valore di tale limite è detto derivata di f in x e si indica in uno dei
seguenti modi:
df (x)
f 0 (x),
, Df (x).
dx
Inoltre si dice che f è derivabile in (a, b) se f è derivabile in ogni
punto x ∈ (a, b)
Sonia L’Innocente
Sonia L’Innocente (Camerino)
5 / 26
Derivate
Vediamo come si calcolano le derivate di alcune semplici funzioni
utilizzando solo la definizione.
Se f (x) = c è una funzione costante con c ∈ R allora f 0 (x) = 0,
dc
cioè Dc = dx
= 0. Infatti
f (x + h) − f (x)
c−c
= lim
= lim 0 = 0
h
h
h→0
h→0
h→0
f 0 (x) = lim
Se f (x) = x allora f 0 (x) = 1, cioè Dx =
f 0 (x) = lim
h→0
dx
dx
= 1. Infatti
x +h−x
h
f (x + h) − f (x)
= lim
= lim = lim 1 = 1
h
h
h→0
h→0 h
h→0
Sonia L’Innocente
Sonia L’Innocente (Camerino)
6 / 26
Derivate
Definizione
Data una funzione f : (a, b) → R e dato x ∈ (a, b), se il seguente limite
f (x + h) − f (x)
,
h
h→0
lim
non esiste o è infinito (±∞) allora si dice che f non è derivabile in x.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
7 / 26
Derivate
Esempi
Vediamo alcuni esempi di funzioni non derivabili in un punto.
1
La funzione f (x) = |x| non è derivabile in 0 infatti
f (0 + h) − f (0)
|h|
= lim
h
h→0
h→0 h
lim
2
e questo limite non esiste.
√
La funzione f (x) = 3 x − 1 non è derivabile in 1 infatti
√
√
3
3
2
f (1 + h) − f (1)
1+h−1
h
lim
= lim
= lim
= lim h− 3
h
h
h→0
h→0
h→0 h
h→0
1
= +∞.
= lim √
3
h→0
h2
Sonia L’Innocente
Sonia L’Innocente (Camerino)
8 / 26
Derivate
Definizione
In alcuni casi, invece del limite completo per h → 0, soltanto il limite
destro h → 0+ , oppure il limite sinistro h → 0− . Nel primo caso si parla
di derivata destra e nel secondo caso, di derivata sinistra. Se f (x) è
una funzione in [a, b], si dice che f derivabile nell’intervallo chiuso
[a, b] se è derivabile in ogni punto x ∈ (a, b), ed inoltre se, f ammette
derivata destra nel punto x = a, e ammette derivata sinistra nel punto
x = b.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
9 / 26
Derivate
Diamo ora una tabella dove ci sono le derivate delle funzioni
elementari
f (x)
c
xb
ex
log x
ax
loga x
f 0 (x)
0
b x b−1
ex
ax
1
x
1
x
log a
loga e
f (x)
sin x
cos x
tan x
arcsin x
arccos x
arctan x
f 0 (x)
cos x
− sin x
1
cos2 x
√1
1−x 2
−√ 1 2
1−x
1
1+x 2
Sonia L’Innocente
Sonia L’Innocente (Camerino)
10 / 26
Derivate
Operazioni e derivazione
Se f (x) e g(x) sono due funzioni derivabili allora anche la loro somma,
differenza, prodotto e quoziente è derivabile nel loro dominio, inoltre
valgono le seguenti formule
D(cf ) = cDf , quando c è una costante
D(f ± g) = Df ± Dg
D(f · g) = Df · g + f · Dg
D( gf ) =
Df ·g−f ·Dg
g2
Sonia L’Innocente
Sonia L’Innocente (Camerino)
11 / 26
Derivate
Osservazione
Vediamo altre formule di derivazione.
Derivazione della funzione composta. Se f e g sono due
funzioni tali che: g è derivabile in x e f è derivabile in g(x) allora
f ◦ g è derivabile in x e
D(f ◦ g)(x) = Df (g(x)) · Dg(x)
Derivazione della funzione inversa. Se f è continua, derivabile
ed invertibile in (a, b) e se Df (y) 6= 0, ∀y ∈ (a, b) allora f −1 è
derivabile in x = f (y), y ∈ (a, b) e si ha
D(f −1 )(x) =
1
Df (y )
dove y = f −1 (x).
Sonia L’Innocente
Sonia L’Innocente (Camerino)
12 / 26
Derivate
Osservazione
Vediamo altre formule di derivazione.
Derivazione della funzione (f (x))g(x) .
g(x)f 0 (x)
g(x)
g(x)
0
D (f (x))
.
= (f (x))
g (x) log(f (x)) +
f (x)
Tale formula può essere evitata utilizzando le regole sopra
esposte e la seguente identità:
(f (x))g(x) = elog(f (x))
g(x)
= eg(x) log(f (x))
Sonia L’Innocente
Sonia L’Innocente (Camerino)
13 / 26
Derivate
Significato geometrico della derivata di una funzione
Significato geometrico della derivata di una funzione
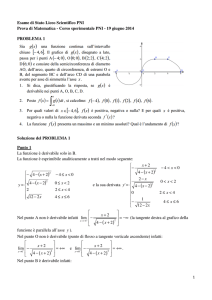
Si noti che se f è una funzione derivabile in x0 allora quando h tende a
0 (h → 0) la retta passante per i punti P = (x0 , f (x0 )) e
Ph = (x0 + h, f (x0 + h)) tende alla retta tangente al grafico di f nel
punto P. Dunque, quando esiste f 0 (x0 ) tale valore coincide con il
coefficiente angolare della retta tangente al grafico di f nel punto P,
vedi Figura successiva (a), e l’equazione di tale retta è
y = f (x0 ) + f 0 (x0 )(x − x0 ).
Sonia L’Innocente
Sonia L’Innocente (Camerino)
14 / 26
Derivate
x0
x0+h0
x0+h1
x0+h2
Significato geometrico della derivata di una funzione
x0
Figure: Retta tangente nel punto (x0 , f (x0 )); (a) la retta tangente ha
coefficiente angolare f 0 (x0 ); (b) la retta tangente è verticale.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
15 / 26
Derivate
Significato geometrico della derivata di una funzione
Esercizi
1
2
3
Determinare la retta tangente al grafico di f (x) = ex nel punto di
ascissa x0 = 0, [Soluzione r : y = x + 1].
Determinare la retta tangente al grafico di f (x) = sin x nel punto di
ascissa x0 = π2 , [Soluzione r : y = 1].
√
Determinare la retta tangente al grafico di f (x) = x + 1 nel
punto di ascissa x0 = −1, [Soluzione r : x = −1].
Sonia L’Innocente
Sonia L’Innocente (Camerino)
16 / 26
Derivate
Teoremi legati alla derivata
Derivabilità e continuità
Se f è derivabile in x allora f è continua in x.
Teorema di Rolle
Se f : [a, b] −→ R è continua in [a, b] e derivabile in (a, b) e se
f (a) = f (b) allora ∃x0 ∈ (a, b) tale che f 0 (x0 ) = 0, cioè esiste un punto
del grafico di ascissa x0 in cui la retta tangente è orizzontale, si veda la
Figura successiva (a).
Teorema di Lagrange
Se f : [a, b] −→ R è continua in [a, b] e derivabile in (a, b) allora
(a)
∃x0 ∈ (a, b) tale che f 0 (x0 ) = f (b)−f
b−a , cioè esiste un punto del grafico
di ascissa x0 in cui la retta tangente è parallela al segmento che
congiunge (a, f (a)) con (b, f (b)), si veda la Figura successiva (b).
Sonia L’Innocente
Sonia L’Innocente (Camerino)
17 / 26
Derivate
Teoremi legati alla derivata
f(a)=f(b)
a
x0
b
a
x0
b
Figure: (a) Rappresentazione grafica del teorema di Rolle; (b)
Rappresentazione grafica del teorema di Lagrange.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
18 / 26
Derivate
Teoremi legati alla derivata
Osservazione
Se f : [a, b] −→ R è tale che f 0 (x) = 0 ∀x ∈ [a, b] allora f (x) =
costante.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
19 / 26
Derivate
Derivate di ordine superiore
Derivate di ordine superiore
Le derivate di ordine superiore si ottengono derivando ulteriormente le
funzioni ottenute.
Derivata seconda di una funzione f : f 00 (x) = D(f 0 (x))
Derivata terza di una funzione f : f 000 (x) = D(f 00 (x))
...
Derivata n-esima di una funzione f : f (n) (x) = D(f (n−1) (x))
Sonia L’Innocente
Sonia L’Innocente (Camerino)
20 / 26
Derivate
Derivate di ordine superiore
Esercizi
1
2
Calcolare f 0 (x), f 00 (x), f 000 (x) quando f (x) = ex . Quanto vale in
questo caso f (n) (x)?
Soluzione: f 0 (x) = f 00 (x) = f 000 (x) = f (n) (x) = ex
Calcolare f 0 (x), f 00 (x), f 000 (x) quando f (x) = sin x. Quanto vale in
questo caso f (n) (x)?
Soluzione: f 0 (x) = cos x, f 00 (x) = − sin x, f 000 (x) = − cos(x),
(−1)k sin x n = 2k
f (n) (x) =
.
(−1)k cos x n = 2k + 1
Sonia L’Innocente
Sonia L’Innocente (Camerino)
21 / 26
Derivate
Uso delle derivate per il calcolo dei limiti
Teorema di De L’Hôpital
Se f , g : A \ {x0 } −→ R sono due funzioni derivabili e tali che
lim f (x) = 0,
x→x0
lim g(x) = 0,
x→x0
oppure
lim f (x) = ±∞,
x→x0
lim g(x) = ±∞,
x→x0
se g 0 (x) 6= 0 ∀x ∈ A \ {x0 } allora
lim
x→x0
f 0 (x)
f (x)
= lim 0
g(x) x→x0 g (x)
se il limite a destra esiste.
Si noti che se il limite a destra non esiste non si può concludere nulla
su quanto valga il limite a sinistra.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
22 / 26
Derivate
Uso delle derivate per il calcolo dei limiti
Osservazione
Tale teorema continua a valere anche se si hanno limiti destri
(x → x0+ ), limiti sinistri (x → x0− ) o limiti ad infinito (x → ±∞).
Esempi
Tutti i limiti seguenti soddisfano le ipotesi del teorema di De L’Hôpital
1.
lim
x→0
2.
lim
x→0
sin x
cos x
= lim
= 1,
x→0
x
1
1 − cos x
sin x
cos x
1
= lim
= lim
= ,
x→0 2x
x→0
2
2
x2
Sonia L’Innocente
Sonia L’Innocente (Camerino)
23 / 26
Derivate
Uso delle derivate per il calcolo dei limiti
Esempi
Tutti i limiti seguenti soddisfano le ipotesi del teorema di De L’Hôpital
3.
ex
ex − 1
= lim
= 1,
x→0 1
x→0
x
lim
4.
1
log(1 + x)
= lim 1+x = 1,
x→0
x→0 1
x
lim
5.
ex
ex
= lim
= +∞,
x→+∞ x
x→0 1
lim
6.
x 3 + 2x + 1
3x 2 + 2
6x
=
lim
= lim
= +∞,
x→+∞ x 2 + x + 1
x→+∞ 2x + 1
x→+∞ 2
lim
Sonia L’Innocente
Sonia L’Innocente (Camerino)
24 / 26
Derivate
Uso delle derivate per il calcolo dei limiti
Il teorema di De L’Hôpital risulta essere un utile strumento per risolvere
∞
. Vediamo come si possono trattare
forme indeterminate del tipo 00 o ∞
altre forme indeterminate.
Sonia L’Innocente
Sonia L’Innocente (Camerino)
25 / 26
Derivate
Uso delle derivate per il calcolo dei limiti
La forma indeterminata 0 · ∞ può essere ricondotta alla forma
indeterminata 00 oppure a ∞
∞ . Infatti se f (x) → 0 e g(x) → ±∞
allora
f (x) · g(x) = f (x)
= g(x)
1
1
g(x)
↓
0·∞
f (x)
↓
↓
0
0
∞
∞
La forma indeterminata +∞ − ∞ può essere ricondotta alla forma
indeterminata 00 . Infatti se f (x) → +∞ e g(x) → +∞ allora
f (x) − g(x) =
↓
+∞ − ∞
1
1
− f (x)
g(x)
1
f (x)·g(x)
↓
0
0
+∞
−∞
0
1 , 1 , (+∞)
Le forma indeterminata
e 00 possono essere
ricondotte ad una delle forme indeterminate sopra descritte nel
seguente modo:
f (x)g(x) = elog(f (x)
Sonia L’Innocente (Camerino)
g(x)
) = eg(x)·log(f (x)) .
Sonia L’Innocente
26 / 26