momento – esercizio n. 4
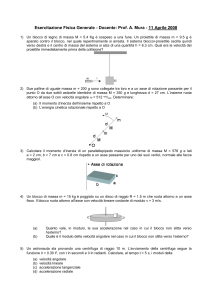
Una barra uniforme di lunghezza L e massa M è imperniata su un asse orizzontale
privo di attrito passante per un suo estremo. La barra è rilasciata da ferma in posizione
verticale. Nell’istante in cui la barra è in posizione orizzontale, trovare.
a. La sua velocità angolare.
b. Il modulo della sua accelerazione angolare.
c. Le componenti x ed y dell’accelerazione del suo centro di massa.
d. Le componenti della forza di reazione del perno.
M⋅ g⋅L 3 g 3
3
3
1
R.:
; ⋅ ; ⋅ g ; ⋅ g ; M⋅ ⋅ g ; M⋅ ⋅ g ;
I
2 L 2
4
2
4
y
y
y
L
L
L
Ry
L/2
θ
θ
x
x
Rx
m·g
ax
x
ay
a) Calcolo della velocità angolare
Sulla barra agiscono solo forze conservative come l’energia potenziale gravitazionale (la
massa M della barra viene considerata concentrata nel centro di massa) e come l’energia
cinetica rotazionale, pertanto:
k f + Uf = K i + Ui
1
L
⋅ I ⋅ ω2f + 0 = 0 + M ⋅ g ⋅
2
2
M⋅ g ⋅L
I
Conoscendo il momento d’inerzia di una barra rettangolare passante per il suo asse, è
possibile ricavare ω f :
M ⋅ L2
I=
3
ωf =
ωf =
M⋅ g ⋅L
3
3⋅g
= M⋅ g⋅L ⋅
=
2
I
M⋅L
L
b) Calcolo del modulo dell’accelerazione angolare
Ricordando che il momento meccanico risultante agente su un corpo libero in moto intorno
ad un certo asse è uguale al prodotto del momento di inerzia rispetto allo stesso asse si
rotazione per l’accelerazione angolare, si ha:
∑ τ = I⋅ α
L M ⋅ L2
=
⋅α
2
3
3 g
α= ⋅
2 L
M⋅ g⋅
1
momento – esercizio n. 4
c) Calcolo delle componenti x ed y dell’accelerazione del suo centro di massa
La componente lungo l’asse x dell’accelerazione del centro di massa è diretta lungo
l’orizzontale negativa e vale proprio l’accelerazione centripeta:
3⋅g L 3
⋅ = ⋅g
a x = ac = ω2f ⋅ R =
L 2 2
La componente lungo l’asse y dell’accelerazione del centro di massa è diretta lungo la
verticale negativa e vale proprio l’accelerazione tangenziale:
3⋅g L 3
a y = at = α ⋅ R =
⋅ = ⋅g
2 ⋅L 2 4
d) Calcolo delle componenti della forza di reazione del perno
Usando l’espressione ∑ F = m·a , particolarizzata per l’asse delle x e delle y si ha:
3
Rx = M ⋅ ax = M ⋅ ⋅ g
2
R y − M ⋅ g = −M ⋅ a y
Ry = M ⋅ g − M ⋅ ay = M ⋅ g − M ⋅
3
1
⋅ g = M⋅ ⋅ g
4
4
2