Principali variabili casuali - Dipartimento di Scienze Sociali ed

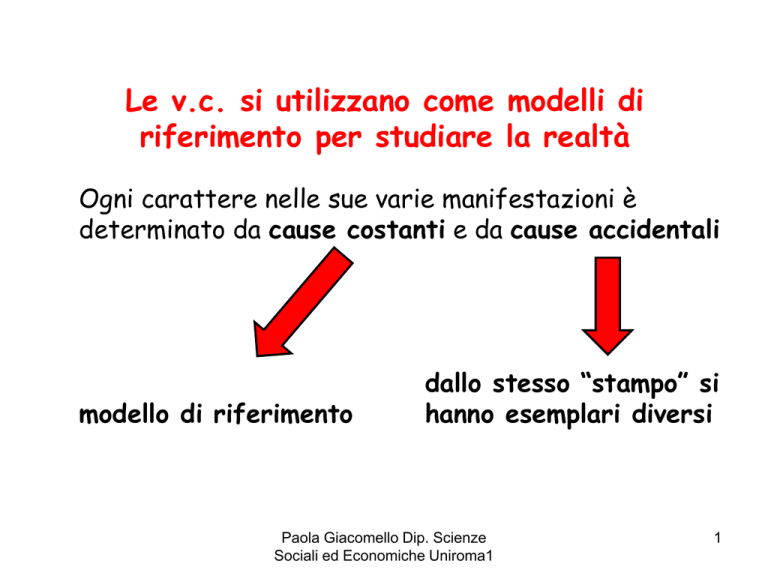
Le v.c. si utilizzano come modelli di
riferimento per studiare la realtà
Ogni carattere nelle sue varie manifestazioni è
determinato da cause costanti e da cause accidentali
modello di riferimento
dallo stesso “stampo” si
hanno esemplari diversi
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
1
Esistono diverse variabili casuali
Variabili discrete
•La variabile bernoulliana
•La variabile binomiale
•La variabile ipergeometrica
Variabili continue
•La variabile di Poisson
•La variabile normale
•etc
•La variabile t di Student
•La variabile Chi-Quadrato
•La variabile F di Snadecor
•etc
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
2
Distribuzione delle stature degli iscritti alla leva dei
nati in Abruzzo e Molise nel 1933
1. Addensamento delle frequenze nelle classi centrali
Paola Giacomello
Scienze
2. Diminuzione delle frequenze
nelleDip.
classi
estreme
Sociali ed Economiche Uniroma1
3
Questo istogramma si può
rappresentare bene
tramite la curva normale o
distribuzione di Gauss
Classe mediana=160-165
Classe modale= 160-165
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
4
Un altro modo per identificare
la distribuzione Normale
https://www.youtube.com/watch?v=FwO2L-oeqIY
Se si misura più volte una stessa grandezza fisica
accontentandosi di una approssimazione grossolana, i
valori che si ottengono sono identici
Se si cerca di avere una precisione elevata l’identità
dei valori svanisce poiché differiscono, seppur di
poco, tra loro
Come valore reale della grandezza si considera la media
delle misure
Gli scostamenti tra ciascuna grandezza e il valor
medio sono detti errori accidentali
Gli errori accidentali si distribuiscono secondo
determinate regole
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
5
Gli errori positivi compensano gli errori
negativi
Intervalli simmetrici rispetto allo 0
contengono circa lo stesso numero di
errori
In valore assoluto gli errori piccoli sono
più frequenti dei grandi ossia le
frequenze diminuiscono al crescere
dell’errore
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
6
From Chaos to Order on the Galton Machine -- A Random Walker
https://www.youtube.com/watch?v=p65aYYuAz-s
Gauss pervenne nel 1809 alla legge che porta il
suo nome, cioè a stabilire che gli errori
accidentali si distribuiscono secondo la curva
normale http://it.wikipedia.org/wiki/Carl_Friedrich_Gauss
Quetelet nel 1835 osservò che le stature ed i
perimetri toracici misurati nelle operazioni di leva
si distribuivano più o meno in modo normale
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
7
La v.c. Normale
è una v.c. continua che può assumere valori su tutto
l’asse reale.
La funzione di densità è data da:
1
f ( x) 
e
 2
1 x
 
2











EX   
-
V  X   2
2>0
2
e = 2,71828 18284 59045 23536 02874 71352 66249 77572 47093
69995...numero di Eulero (in Italia numero di Nepero) funzione
esponenziale
Paola Giacomello Dip. Scienze
8
Π = 3,14 rapporto tra la circonferenza
e
il
diametro
di
un
cerchio
Sociali ed Economiche Uniroma1
La v.c. Normale Standardizzata Z
Se la v.c. X ha una distribuzione
normale con parametri  e 2,
allora Z= (X- )/  è ancora una
v.c. Normale con media nulla e
varianza unitaria.
1
f(z) 
2
z2

e 2
0,30
0,15
0,95
0,00
-1,96
0,00
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
1,96
9
Distribuzione Normale
(confronti con la normale standardizzata varianza diversa)
 

0,75
0,60
0,45
N(0;1)
0,30
 

 

0,15
 

0,00
-4,5
-3,0
-1,5
0,0
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
1,5
3,0
4,5
10
Distribuzione Normale
(confronti con la normale standardizzata media diversa)
0,45
=0
=1 =2
=3
0,0
1,5
3,0
=4
=5
0,30
0,15
0,00
-1,5
4,5
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
6,0
7,5
11
Teorema del limite centrale
Sia X 1, X 2 , X 3 ,... una successione di variabili
casuali indipendenti e identicamente distribuite,
con media  e varianza  2 finite, posto
1
Xn 
n
si ha che la v.c.
Zn

X

n
X
i
i 1
n
 

n
converge in distribuzione, per n   , alla v.c.
Normale standardizzata.
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
12
Supponiamo che il risultato ottenuto dagli studenti
all’esame di statistica sia distribuito normalmente con μ=
73 e σ= 8
• qual è la probabilità di conseguire una votazione non
superiore a 91? P(X ≤ 91)
I STEP standardizzare il valore dell’ascissa per
poter entrare nelle tavole della N(0,1)
(91-73)/8 = 2,25
P(X ≤ 91) = P(Z ≤ 2,25)
II STEP disegnare sulla N(0,1) l’area che
ci interessa
III STEP entrare nella tavola Φ(z)
e leggere in corrispondenza della
riga 2,2 incrocio colonna
0,05 il valore all’interno
= 0,9878
Paola Giacomello Dip. Scienze
Sociali ed Economiche Uniroma1
2,25
13