modello neurofisiologico dei possibili processi cerebrali

FACOLTA’ DI SCIENZE MM.FF.NN.
Corso di Laurea in Scienze dell’Informazione
MODELLO NEUROFISIOLOGICO DEI POSSIBILI PROCESSI
CEREBRALI DETERMINANTI DIFFERENTI CAPACITÀ IN
TERMINI DI MEMORIA DI LAVORO
TESI DI LAUREA DI :
EMILIANO SPERA
RELATORE:
PROF. DOMENICO TEGOLO
CORRELATORE
DOTT. MICHELE MIGLIORE
Matricola:
ANNO ACCADEMICO 2011 - 2012
1
Indice:
Introduzione
pag 4
capitolo 1:
1.1
Introduzione
pag 6
1.2
Modelli per la memoria di lavoro
pag 7
1.3
Il modello multi-componenziale
pag 10
1.4
Memoria di lavoro e altre capacità cognitive, natura e
obiettividella ricerca
pag 13
Capitolo 2:
2.1
introduzione
2.2
Individual Differences in Working Memory Capacity and
pag 14
Episodic Retrieval: Examining the Dynamics of Delayed
and Continuous Distractor Free Recall
pag 14
2.2.1 selezione dei partecipanti all’esperimento
pag 14
2.2.2 modalità dell’esperimento
pag 16
2.2.3 risultati della sperimentazione
pag 16
Capitolo 3:
3.1
introduzione
pag 19
3.2
l’ippocampo e la memoria di lavoro
pag 19
3.3
potenziamento sinaptico e memorizzazione di informazioni
pag 22
3.4
codifica degli oggetti nei neuroni CA1
pag 23
3.5
propagazione dei potenziali d’azione nel neurone e
processo di riconoscimento di un oggetto
pag 24
3.6
il modello
pag 25
3.7
risultati
pag 27
Capitolo 4:
2
4.1
introduzione
pag 30
4.2
I dati sperimentali
pag 30
4.3
trattamento dei dati sperimentali
pag 31
4.4
le simulazioni
pag 32
4.5
simulazioni e dati sperimentali a confronto
pag 34
4.6
dallo spazio parametrico (λ,A) allo spazio delle proprietà
4.7
fisiologiche (n-pla, rumore sul potenziale di membrana)
pag 36
conclusioni
pag 38
AppendiceA (codice)
pag 40
Bibliografia
pag 46
3
INTRODUZIONE
Dalla metà dello scorso secolo è nata un’intensa attività nella comunità
scientifica sui modelli e sui metodi per modellare il processo mnemonico
relativo alla memoria di lavoro.
I test psicologici hanno dimostrato come questo processo mnemonico sia
centrale per lo svolgimento di un gran numero di attività che svolgiamo
quotidianamente, questo motiva la grande attività scientifica in questa direzione.
Nonostante esista una vastissima letteratura che tratta i meccanismi della
memoria di lavoro, fin ora vani sono stati i contributi capaci di ipotizzare i
processi neurofisiologici coinvolti in tali meccanismi.
Questo contributo intende proporre una prima analisi di tale processo
mnemonico e inoltre tiene conto dei processi neuro-fisiologici in esso coinvolti.
La tesi fa riferimento all’analisi condotta da Unsworth in [40] e dal modello
neuro-computazionale per la memorizzazione di oggetti in una lista sviluppato
in [37] .
Il lavoro di Unsworth ha svelato come esista una dipendenza tra le prestazioni
ottenute in esperimenti di rievocazione libera e la bontà della memoria di lavoro
dei soggetti sottoposti alla sperimentazione. Partendo da questa relazione e dalla
modellazione proposta in [37] siamo riusciti a sviluppato un’ipotesi sulla
differenziazione, in termini fisiologici, che intercorre tra soggetti con buone
capacità nella memoria di lavoro e i soggetti con scarse capacità.
La tesi è stata strutturata in quattro capitoli, il primo capitolo è stato dedicato
alla memoria di lavoro dal punto di vista psicologico, fornendo alcune delle
definizioni e dei modelli di natura psicologica più accreditati, e sono state
introdotte alcune relazioni che intercorrono tra memoria di lavoro e altre
capacità cognitive.
4
Nel secondo capitolo saranno proposti i dati sperimentali presentati da Unsworth
con la relativa analisi dei dati.
Un’analisi dei processi cerebrali coinvolti nei meccanismi relativi alla memoria
di lavoro saranno presentati nel terzo capitolo. In esso sarà data una descrizione
della regione ippocampale e i flussi di informazione che si sviluppano al suo
interno, si focalizzerà quindi l’attenzione sui neuroni della famiglia CA1 per poi
presentare il modello,proposto in [37], per la memorizzazione di oggetti da una
lista.
In fine nel quarto capitolo mostreremo un’analisi dei risultati ottenuti tramite il
modello descritto, e si svilupperanno le motivazioni che hanno condotto
all’identificazione
delle
caratteristiche
fisiologiche
che
maggiormente
intervengono nel determinare le differenti capacità dei soggetti in termini di
memoria di lavoro.
5
CAPITOLO 1
1.1 Introduzione
I primi studiosi che si occuparono del processo di memorizzazione cercarono di
spiegarlo nei termini di un singolo processo unitario, esattamente come
tentavano di spiegare i processi di apprendimento. Negli anni successivi gli
psicologi iniziarono a proporre modelli relativi a specifici aspetti della memoria,
giungendo così a formulare teorie multiprocesso e multimodali della memoria
umana che appariva, quindi, composta da vari sistemi interconnessi.
Una prima e fondamentale distinzione tra i vari processi mnemonici fu proposta
dal neurofisiologo Donald O. Hebb, il quale ipotizzò l’esistenza di una doppia
traccia: una responsabile di una registrazione "a breve termine" della durata di
pochi secondi o minuti e una seconda che subentra alla prima e che codifica le
informazioni in forma stabile e duratura. Hebb propose anche uno dei principi
cardine su cui si fondano i processi di memorizzazione ossia il "principio di
convergenza sincronica" secondo il quale due cellule o sistemi che
ripetutamente si mostrino attivi al tempo stesso tenderanno a divenire "associati"
in modo che l’attività dell’uno faciliti quella dell’altro.
Le intuizioni di Hebb furono poi confermate sperimentalmente da diversi studi
divenendo il punto di partenza per ogni analisi sui processi mnemonici che si
sarebbero sviluppati in futuro.
Le due differenti tipologie di memoria individuate da Hebb si distinguono oltre
che per la differente durata temporale anche per la capacità di immagazzinare
informazioni.
La memoria primaria o a breve termine infatti presenta una capacità limitata,
come è stato mostrato sperimentalmente da George Miller [29] un individuo può
elaborare e trasmettere circa sette unità per volta, mentre la memoria a lungo
termine ha una capacità sostanzialmente illimitata.
6
Con lo sviluppo della neuropsicologia nacquero quindi vari modelli che
miravano all’unificazione delle precedenti ricerche sui vari processi di
memorizzazione, al fine di spiegare le componenti e l’organizzazione della
memoria stessa.
Con il susseguirsi di ricerche sempre più specifiche e con l’avvicendarsi di
differenti teorie, vennero messi a fuoco diversi tipi di memoria, le loro relative
componenti e le interazioni tra i sistemi coinvolti.
Negli anni successivi alla classificazione proposta da Hebb si svilupparono altre
classificazioni che tennero conto della fisiologia delle diverse memorie. Alcune
delle più importanti tipologie di memoria che sono state identificate sono la
memoria procedurale o implicita, la memoria semantica, la memoria episodica,
la memoria visiva, la memoria iconica, quella uditiva e quella motoria.
Un’altra tappa fondamentale nello studio dei processi mnemonici si ebbe grazie
al lavoro di Baddeley e Hitch [6 ] che partendo dalla grande distinzione tra
memoria a lungo termine e memoria a breve termine svilupparono il concetto di
memoria di lavoro : un sistema per il mantenimento temporaneo e per la
manipolazione dell’informazione durante l’esecuzione di differenti compiti
cognitivi.
In questo capitolo analizzeremo questo tipo di memoria con un’analisi più
approfondita mostrando i principali punti di contatto dei modelli (di natura
psicologica) più affermati proposti in letteratura
per poi presentare nello
specifico il modello multi-componenziale .
1.2 Modelli per la memoria di lavoro
Nella storia delle Neuroscienze cognitive molti sono stati gli studiosi che hanno
cercato di dare una definizione della memoria di lavoro.
7
Baddeley e Logie due dei più affermati studiosi dei processi mnemonici l’hanno
definita come: “l’insieme di componenti cognitive che consentono agli individui
di comprendere e rappresentarsi mentalmente il loro ambiente circostante, di
mantenere le informazioni sulle loro esperienze recenti, di sostenere
l’acquisizione di nuove conoscenze, di risolvere problemi e di formulare,
collegare e raggiungere obiettivi specifici e attuali” [7].
Questa particolare tipologia di memoria è stata negli anni molto studiata e
analizzata e molti sono stati i modelli che hanno tentato di spiegarne il
funzionamento. Tra questi, il primo e sicuramente il più studiato, citato, criticato
e correlato anatomicamente fu quello elaborato da Baddeley e Hitch [5,6] .
L’interesse del mondo scientifico nei confronti della memoria di lavoro nasce
dalla molteplicità e dalla varietà dei compiti in cui è coinvolta, si è visto ad
esempio che è in relazione con la capacità di apprendimento di un vocabolario
[11,12], o ancora con la capacità di imparare un linguaggio di programmazione
[21,36] così come con le performance nei test attitudinali scolastici (S.A.T.)
[39].
Inoltre diversi lavori in letteratura hanno mostrato l’esistenza di un legame tra la
bontà della memoria di lavoro degli individui e la loro capacità nelle abilità
fluide [1,9,13,19,20,41].
È proprio l’eterogeneità delle funzioni in cui è coinvolta che ha determinato una
difficoltà nel dare una definizione unanimemente condivisa della memoria di
lavoro.
Questa difficoltà nel determinare una definizione universalmente accettata della
memoria di lavoro ha stimolato un’interessante analisi da parte di Miyake e
Shah [27] i quali attraverso un confronto tra i più accreditati modelli di Mdl
proposti in letteratura hanno individuato una serie di punti comuni che
caratterizzano tutti i modelli.
I punti di consenso dei diversi modelli trovati sono:
8
1. La MdL non è concepita come una
“box” per il mantenimento di
informazioni a breve termine strutturalmente separata dagli altri sistemi di
memoria o cognitivi;
2. La MdL è al servizio di attività cognitive complesse, quali il making
decision, il problem solving e così via;
3. Il “controllo” e la “regolazione” della MdL dipendono dal monitoraggio e
dall’aggiornamento, ma anche dall’inibizione attiva delle informazioni
presenti in MdL;
4. La MdL è a capacità limitata;
5. La MdL non è completamente unitaria e dominio-generale;
6. Le conoscenze in memoria a lungo termine (MLT) giocano un ruolo
determinante nelle prove di MdL.
Partendo da questi 6 punti di consenso generale Miyake e Shah [27] hanno
proposto una definizione di MdL onnicomprensiva, che unifica i modelli di MdL
presi in considerazione.
Miyake e Shah forniscono la seguente definizione:
“La memoria di lavoro comprende i meccanismi o processi che sono coinvolti
nel controllo, nella regolazione e nel mantenimento attivo di informazioni
rilevanti per l’esecuzione di compiti cognitivi complessi, siano essi nuovi o
familiari e ben appresi. Essa non è una “scatola” e nemmeno ha una “sede” fissa
all‟interno dell’architettura cognitiva. Non è un sistema completamente unitario,
in quanto comprende molteplici codici di rappresentazione e/o differenti
sottosistemi. I limiti di capacità della MdL sono legati a vari fattori e devono
essere visti come una proprietà emergente dei diversi processi e meccanismi
coinvolti. La MdL è strettamente legata alla MLT, e i suoi contenuti consistono
essenzialmente in rappresentazioni attivate dalla MLT, ma possono anche
9
estendersi a rappresentazioni che possono essere rapidamente riattivate dalla
MLT mediante segnali di recupero” .
1.3 Il modello multi-componenziale
Il modello multi-componenziale proposto da Baddeley e Hitch [6] ipotizza che
la MdL sia composta da un sistema attentivo di controllo, il sistema Esecutivo
Centrale, che supervisiona e coordina un insieme di sistemi sussidiari o
periferici, tra cui i più studiati sono il Loop Articolatorio e il Taccuino Visuospaziale.
Il primo è deputato al mantenimento e all’elaborazione di informazioni verbali e
acustiche, mentre il secondo è responsabile del mantenimento e della
manipolazione di materiale visuo-spaziale .
Baddeley [5] ha successivamente ampliato il modello, con l’aggiunta
dell’episodic
buffer,
un’ulteriore
componente
capace
di
integrare
le
informazioni che provengono dai due sotto-sistemi con quelle della MLT, sotto
il controllo dell’esecutivo centrale.
Ognuna delle componenti della MdL assolve un compito specifico e ha delle
caratteristiche differenti. Il sistema esecutivo centrale è volto alla selezione di
strategie, alla presa di decisioni o ancora all’integrazione di informazioni
provenienti da diverse fonti. Secondo Baddeley [3,4], l’esecutivo centrale deve
essere considerato come un sistema attentivo piuttosto che un magazzino di
memoria ed è un sistema a capacità limitata come la MdL e quindi può essere
sovraccaricato da compiti che richiedono un carico attentivo oneroso.
Il loop articolatorio, uno dei due sistemi sussidiari regolati dall’ esecutivo
centrale, ha il compito di memorizzare informazioni verbali ed è composto da
due diverse componenti:
10
1)Magazzino fonologico in grado di
mantenere l’informazione linguistica.
2)Processo di controllo articolatorio.
.
Le tracce delle informazioni contenute nel magazzino fonologico decadono
rapidamente, tuttavia è possibile mantenere più a lungo le informazioni
attraverso la ripetizione subvocalica, la quale consente di mantenere la traccia
per poter essere successivamente riutilizzata.
L’altro sistema sussidiario, il taccuino visuo-spaziale , o memoria di lavoro
visuo-spaziale (MLVS), invece è deputato al mantenimento e all’elaborazione di
materiale visivo e spaziale.
Logie [23] considera il taccuino visuo-spaziale composto da due magazzini a
breve termine, uno visivo e l’altro spaziale. Il primo è soggetto al decadimento e
all’interferenza da parte di nuove informazioni e permette l'elaborazione di
oggetti e delle loro caratteristiche visive mentre il secondo è un sistema deputato
alla pianificazione del movimento e assolve il suo compito avvalendosi delle
informazioni presenti nell’altro magazzino.
Molti studiosi considerano la MLVS come una componente della memoria
complementare al Loop Articolatorio [3,22,23]. Quest’interpretazione nasce dal
fatto che, nonostante le ricerche non hanno dimostrato una completa analogia tra
MdL verbale e visuo-spaziale, una serie di studi hanno riscontrato nella MLVS
alcuni effetti simili a quelli presenti nel Loop Articolatorio [10,24,25,35].
Ad esempio si può osservare come sia nella MdL Visuo-spaziale che in quella
verbale, in presenza di stimoli simili tra loro, si riscontra più difficoltà
nell’operazione di ricordo. O ancora come per entrambe le tipologie di memoria
si verifica che se viene presentato materiale di sottofondo in concomitanza ad un
compito di memorizzazione si ha una compromissione della prestazione.
Sebbene il modello multicomponenziale di MdL sembrasse offrire spiegazioni
plausibili ad un ampia serie di dati provenienti sia da adulti sani che da pazienti
neurologici, esso presentava una serie di problemi legati all’interazione tra MdL
11
e MLT, dovuti all’assunzione che l’Esecutivo Centrale fosse esclusivamente un
sistema attentivo, o alla mancanza di una componente in grado di far interagire il
Loop Fonologico ed il Taccuino Visuo-spaziale. Questi ed altri problemi
spinsero Baddeley [5] ad introdurre nel modello l’episodic buffer (Figura 1), un
ulteriore processo o meccanismo in grado di combinare sinergicamente
informazioni provenienti dai vari sottosistemi sottoforma di rappresentazione
temporanea.
Figura 1 Rappresentazione schematica del modello multi-componenziale di Mdl proposto da Baddeley nel 2000
Baddeley [5] ritiene che l’Episodic Buffer sia in grado di immagazzinare
informazioni in un codice multidimensionale, fornendo così un’interfaccia
temporanea tra i servo-sistemi (il Loop Articolatorio e il Taccuino Visuospaziale) e la MLT. Si presume che sia controllato dall’Esecutivo Centrale e che
è responsabile dell’integrazione di informazioni da differenti fonti in
rappresentazioni consapevoli. L’Episodic Buffer permette, quindi, non solo di
modellare l’ambiente circostante, ma anche di creare nuove rappresentazioni
cognitive in grado di facilitare la risoluzione di problemi.
12
1.4 Memoria di lavoro e altre capacità cognitive, natura e obiettivi della
ricerca
In definitiva la memoria di lavoro è determinante per una serie di compiti che gli
esseri umani svolgono quotidianamente ed influenza in modo significativo
moltissime capacità.
È questa trasversalità che rende centrale la comprensione del funzionamento del
processo mnemonico, in quanto la comprensione del meccanismo sottostante
potrebbe rendere possibile intervenire sullo stesso per ottenerne un
miglioramento prestazionale e di conseguenza un miglioramento prestazionale
su tutti i processi ad esso collegati.
Se, come abbiamo visto, esistono molti modelli psicologici che tentano di
descrivere la memoria di lavoro non esistono modelli che tengano conto dei
processi fisiologici alla base di questo processo cerebrale.
L’obiettivo della tesi è stato quindi, partendo da dati sperimentali ottenuti da
Unsworth in esperimenti di rievocazione libera (free recall) su soggetti con
differenti capacità di memoria di lavoro, costruire un modello neurofisiologico
in grado di riprodurre i dati sperimentali e da questo riuscire ad individuare le
differenze fisiologiche che determinano una maggiore o minore capacità della
memoria di lavoro nei diversi individui.
13
CAPITOLO 2
2.1 Introduzione:
In questo capitolo presenteremo i dati sperimentali a cui ci si riferisce per la
formalizzazione del modello.
Nel seguito verrà dettagliato l’articolo “Individual Differences in Working
Memory Capacity and Episodic Retrieval: Examining the Dynamics of Delayed
and Continuous Distractor Free Recall” [40]. In esso sono presentati i risultati
che evidenziano, tramite esperimenti di tipo psicologico, la tempistica
elaborativa del cervello umano al fine di recuperare informazioni dalla memoria
di lavoro.
2.2 Individual differences in working memory capacity and episodic
retrieval: examining the dynamics of delayed and continuous distractor free
recall
2.2.1Selezione dei partecipanti all’esperimento:
la prima fase dell’esperimento consiste in una pre-selezione dei partecipanti,
seguendo una procedura standard, classificando i soggetti in funzione di tre
diverse misure rappresentative della qualità della memoria di lavoro.
1) Test su operazioni matematiche:
I partecipanti sono tenuti a risolvere una serie di operazioni matematiche e tra
un’operazione e l’altra vengono presentate delle lettere indipendenti per un
intervallo di tempo di 1 secondo.
I partecipanti sono successivamente tenuti a richiamare le lettere presentate
nel corretto ordine.
14
Il punteggio è dato dalla percentuale di lettere corretti posizionati nella
posizione corretta.
2) Test su operazione di lettura:
I partecipanti sono tenuti a leggere una serie di frasi e tra una frase e l’altra
gli vengono proposte delle lettere indipendenti.
In questo test i partecipanti devono leggere una frase e verificarne la
sensatezza.
La metà delle frasi aveva un senso e l'altra metà no.
Le frasi senza senso sono state ottenute con la semplice sostituzione di una
parola da una frase altrimenti sensata. Dopo che i partecipanti hanno indicato
se la frase ha senso, la lettera gli viene presentata soltanto per 1 secondo.
Anche in questo test i partecipanti erano quindi tenuti a ricordare le lettere
presentate nel loro corretto ordine.
Infine il punteggio sarà calcolato in maniera analoga al test precedente.
3) Test su operazioni di identificazione di simmetria:
In questo test ai partecipanti è richiesto di ricordare una sequenza di quadrati
rossi presentati all’interno di una matrice.
Ai soggetti vengono proposte delle matrici 8*8 su di esse i partecipanti
devono valutare la simmetria, dopo ogni valutazione viene loro presentata
una matrice di dimensioni 4*4 per un tempo di 650 ms in cui un riquadro è
colorato di rosso.
Infine i partecipanti saranno tenuti ad indicare la sequenza ordinata delle
celle presentate in rosso all’interno della matrice.
Anche in questo caso il punteggio è dato dalla percentuale delle posizioni
individuate correttamente e nella posizione opportuna all’interno della
sequenza.
15
I test sono stati proposti a più di 600 individui al fine di individuare, in funzione
dei risultati, 25 soggetti classificati come soggetti con alte capacità mnemoniche
e 20 classificati come soggetti con basse capacità mnemoniche.
2.2.2 Modalità dell’esperimento:
Ai partecipanti selezionati per l’esperimento sono state presentate 21 liste di
parole di lunghezza variabile (6,9 o 12 parole).
Le parole sono state presentate solo per 1″ ciascuna e i partecipanti
erano tenuti a leggere ogni parola ad alta voce.
Dopo la presentazione della lista, i soggetti sono stati impegnati per 20″ in
attività che li distraessero prima dell’operazione di ricordo.
Dopodiché i partecipanti hanno avuto 45″ per ricordare il maggior numero di
parole possibili, in qualsiasi ordine loro volessero.
Per ogni risposta si è quindi registrato quando la risposta è stata data .
2.2.3 Risultati della sperimentazione:
Nell’articolo vi è un’analisi dei dati da vari punti di vista.
Vengono misurate in funzione della lunghezza della lista e della categoria
d’appartenenza dei soggetti su cui è stato condotto l’esperimento varie misure
d’interesse come ad esempio: la percentuale di parole ricordate, la percentuale di
ricordi errati, la media dei tempi impiegati per ricordare le parole e le
distribuzioni delle latenze cumulative.
I risultati riportati in [40] relativi alle distribuzioni delle latenze cumulative sono
stati considerati di particolare interesse e rappresentano il punto di partenza del
lavoro di questa tesi.
16
Unsworth mostra come i dati relativi al numero di parole ricordate in funzione
del tempo siano ben fittabili attraverso una esponenziale cumulativa (fig. 2):
Dove: A è il valore asintotico a cui tende l’esponenziale per t tendente a infinito
è un parametro che indica la rapidità con cui cresce la funzione
t è la variabile tempo
Figura 2 grafici proposti da Unsworth in cui vengono riportati i dati sperimentali e le curve tramite le quali
sono fittati per esperimenti condotti utilizzando liste composte da 6, 9 e 12 parole
Inoltre tramite l’utilizzo di test statistico non parametrico di KolmogorovSmirnov si è verificata che la differenza tra i dati sperimentali fittati e la
distribuzione definita dall’esponenziale cumulativa non è significativa sia per i
soggetti con buone capacità mnemoniche sia per i quelli con cattive capacità
mnemoniche, e per gli esperimenti condotti per tutte le diverse lunghezze delle
liste.
L’articolo mostra come gli individui con migliori capacità mnemoniche
ricordano un numero maggiore di parole e di conseguenza come le latenze
17
cumulative associate a questi soggetti siano fittate da esponenziali cumulative
con asintoto “A” più alto.
Inoltre per questi soggetti è stata riscontrata una capacità di raggiungere gli
asintoti in maniera più rapida e quindi un valore maggiore del parametro λ nella
esponenziale cumulativa che fitta i dati relativi ai loro test.
Successivamente sono stati fittati anche i dati ottenuti come media dei risultati
degli esperimenti raggruppandoli secondo le due categorie di individui,
ricavando i seguenti parametri per le relative esponenziali cumulative (tab1):
Parametro λ:
capacità mnemonica
parametro A:
(lunghezza lista)
valore asintotico del numero rapidità
con
cui
di parole ricordate
ricordano le parole
Bassa (6)
3,39
0,10
Alta (6)
4,19
0,16
Bassa (9)
4,57
0,08
Alta (9)
5,48
0,12
Bassa (12)
5,24
0,07
Alta (12)
6,10
0,10
CAPI
Tab 1: valore dei parametri A e λ delle esponenziali cumulative che fittano al meglio i dati sperimentali ottenuti
mediando tutti i dati relativi alle differenti tipologie di esperimenti
18
si
CAPITOLO 3
3.1 Introduzione:
In questo capitolo saranno presentate le zone del cervello e le famiglie di
neuroni coinvolte nella memoria di lavoro. Inoltre saranno evidenziati i
meccanismi fisiologici che permettono l’apprendimento e il ricordo di un
generico oggetto.
Passeremo quindi alla presentazione del nostro modello e faremo un riepilogo
esaustivo dei risultati ottenuti in [37]
3.2 l’ippocampo e la memoria di lavoro
Il cervello umano è un organo molto complesso, il suo tessuto è composto da
unità fondamentali chiamate neuroni, che si diversificano in funzione della loro
posizione e del loro compito.
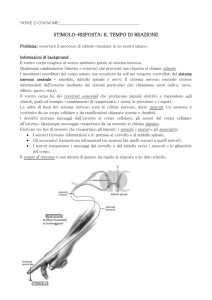
Diversi studi hanno mostrato come l’ippocampo sia la regione cerebrale
principalmente coinvolta nei processi relativi alla memoria di lavoro [38,2,33] ,
e come i neuroni della famiglia CA1, in funzione delle loro caratteristiche
fisiologiche [32] e della loro particolare posizione all’interno della zona
ippocampale [18], possano essere identificati come le unità atte al
riconoscimento degli oggetti da ricordare quando si utilizza la memoria di
lavoro [31].
I neuroni della famiglia CA1 sono neuroni con una struttura piramidale (figura
3), e come per la maggior parte delle cellule neuronali nella sua struttura si
possono distinguere 3 parti morfologicamente e funzionalmente distinte: i
dendriti (classificati in funzione della posizione nella cellula) che hanno forma
filamentosa e fungono da terminali di input della cellula, il soma che ha il
19
compito di elaborare gli stimoli che arrivano in input e gli assoni che fungono da
terminale di output della cellula.
I neuroni di questa famiglia hanno dimensione dell’ordine di grandezza delle
centinaia di μm e sono caratterizzati dalla presenza di un solo assone, da uno o
più dendriti apicali (i piu lontani dal soma), da diversi dendriti
obliqui
(distribuiti lungo la cellula tra il soma e i deneriti apicali), caratterizzati da
dimensioni inferiori alla media, e da molti dendriti basali (posizionati alla base
del neurone in prossimità del soma) [17].
I dendriti obliqui hanno un ruolo fondamentale nel funzionamento del neurone
in quanto fungono da terminali di input, su di essi infatti arrivano i potenziali
d’azione provenienti dai neuroni della famiglia CA3.
Figura 3 ricostruzione tramite NEURON di un neurone CA1
Un altro aspetto che caratterizza fortemente i neuroni della famiglia CA1 è la
loro collocazione spaziale, questi sono il terminale di output del processo di
elaborazione delle informazioni che si ha nella regione ippocampale.
20
È infatti noto che l’informazione nella regione ippocampale compia il seguente
iter (figura 4): il segnale di input viene trasmesso dalla corteccia entorinale ai
Dentate Gyrus e ai CA3 tramite il Perforant Path, i CA3 inoltre ricevono anche
un altro input dai Dentate Gyrus attraverso le Mossy Fibers.
I CA3 mandano quindi un segnale di output tramite l’assone ai neuroni CA1,
attraverso il Schaffer Collateral Pathway, i quali ricevono contemporaneamente
degli input sui dendriti distali dalla corteccia entorinale via Perforant path .
Gli assoni dei neuroni CA1 infine mandano il loro output alla corteccia
entorinale e al subiculum.
Figura 4 flusso delle informazioni nell'ippocampo
21
3.3 Potenziamento sinaptico e memorizzazione di informazioni
È importante sottolineare che, durante la vita di ogni neurone, le sinapsi sono in
continua mutazione, viene indicata col termine plasticità sinaptica questa
fondamentale capacità del sistema nervoso di modificare l'efficienza del
funzionamento delle sinapsi, di instaurarne di nuove e di eliminarne alcune.
Questa proprietà permette al sistema nervoso di modificare la sua funzionalità e
la sua struttura in modo più o meno duraturo in funzione degli input esterni.
In funzione del nostro lavoro è importante evidenziare come questa sia la
proprietà neurobiologica che sta alla base del fenomeno della memoria e dei
processi di apprendimento.
Più in particolare il processo che si pensa sia alla base dei processi di
apprendimento è quello del potenziamento sinaptico.
Quello che succede in questo processo dal punto di vista fisiologico è che in
presenza di stimolazioni pre-sinaptiche a frequenze elevate, chiamate
stimolazioni tetaniche (processi riscontrati in molte cellule nervose), viene
indotto un’aumento dell'ampiezza dei "potenziali eccitatori post-sinaptici"
(excitatory postsynaptic potential, EPSP).
Tramite il potenziamento sinaptico possiamo quindi indurre un neurone a
rispondere con maggiore eccitazione a stimoli provenienti da alcune sinapsi
piuttosto che da stimoli provenienti da altre.
Inoltre, poiché all’interno del nostro sistema nervoso gli oggetti che
costituiscono la realtà sono rappresentati come insiemi di potenziali d’azione
che si trasmettono attraverso le reti neuronali tramite interazioni sinaptiche, è
facile intuire come il potenziamento di una n-pla di sinapsi su un neurone
corrisponda a rendere quel neurone maggiormente eccitabile in funzione della
stimolazione attraverso una particolare n-pla di potenziali d’azione.
22
Questo corrisponde alla capacità di quel neurone di rispondere con maggiore
intensità alla codifica di un particolare oggetto ossia alla capacità di
“riconoscere“ l’oggetto.
È tramite questo meccanismo di sintonizzazione di un neurone su un particolare
oggetto che si attua il processo di memorizzazione.
3.4 Codifica degli oggetti nei neuroni CA1
Un qualsiasi oggetto quindi può essere rappresentato, nella comunicazione tra
neuroni, tramite un insieme di potenziali d’azione indirizzati a specifiche sinapsi
.
In particolare nell’ippocampo i neuroni della famiglia CA1 ricevono un insieme
di potenziali d’azione sui loro dendriti obliqui dai neuroni della famiglia CA3
[8,28].
In questo processo, le interazioni sinaptiche su sinapsi in precedenza potenziate,
potranno determinare dei potenziali d’azione locali nei dendriti obliqui dei CA1
[30,26,14], segnali che potrebbero diffondersi all’interno di tutto il neurone [15]
e così determinare un potenziale d’azione nel soma che si propagherà attraverso
l’assone in altre regioni cerebrali. Nel processo di trasmissione di informazioni
dai neuroni CA3 ai neuroni CA1 possiamo, quindi, pensare che gli oggetti siano
rappresentati dal sottoinsieme dei dendriti obliqui del neurone CA1 su cui
arrivano i potenziali d’azione dai neuroni CA3. Poiché inoltre è noto che gli
oggetti vengono riconosciti non come elementi unitari, ma come unione dei
propri elementi caratterizzanti, potremmo ipotizzare, nel codificare un oggetto
tramite una n-pla di obliqui, di associare ogni elemento caratterizzante
dell’oggetto ad un diverso obliquo.
23
Potremmo ad esempio codificare un volto tramite una tripla di obliqui
associando i tre obliqui rispettivamente a occhi, naso e bocca (figura 5).
Figura 5 schematizzazione di un’ipotesi di rappresentazione dei volti nella comunicazione tra neuroni CA3 e CA1
3.5 Propagazione dei potenziale d’azione nel neurone e processo di
riconoscimento di un oggetto
Gli elementi determinanti per la formazione di un potenziale d’azione nel soma
in un neurone CA1 stimolato su una n-pla di sinapsi sono principalmente 2:
- il numero e le posizioni dei dendriti obliqui nei quali si determinano potenziali
d’azione locali
- il rumore di sottofondo di membrana [31].
Se il primo dipende dalla codifica dell’oggetto su cui è accordato il neurone e
dal segnale che arriva in input, il secondo nasce a causa dell’attività di centinaia
24
di migliaia di sinapsi eccitatorie ed inibitorie presenti sulla membrana cellulare
dei neuroni della famiglia CA1.
In accordo con gli studi proposti da Quiroga che vede il potenziale d’azione di
un particolare neurone come l’elemento associato al ricordo di un oggetto [34].
Nel nostro modello il ricordo di un oggetto memorizzato in precedenza si avrà
quando il neurone sintonizzato su esso verrà stimolato sugli obliqui che
codificano l’oggetto stesso. Negli obliqui stimolati si determineranno infatti
potenziali d’azione che propagandosi lungo il neurone, sotto opportune
condizioni di rumore di membrana, determineranno un potenziale d’azione nel
soma che corrisponderà al ricordo .
3.6 Il modello
Il modello proposto in [37] si basa quindi sull’idea che nel processo di
memorizzazione viene associato un neurone, tramite il potenziamento sinaptico,
ad ogni parola che viene memorizzata.
Inoltre il modello prevede che nella fase di recupero dell’informazione
memorizzata si abbia una stimolazione di n-ple casuali di sinapsi, posizionate
sui dendriti obliqui, tramite potenziali d’azione che codificano parole casuali.
Osservazioni sperimentali mostrano che la regione ippocampale in cui sono
localizzati i neuroni della famiglia CA1 è stimolata con una frequenza
caratteristica γ pari a circa 60 hz.
Nelle nostre simulazioni abbiamo quindi assunto che i neuroni della famiglia
CA1 ricevano in input una differente n-pla casuale di potenziali d’azione sui
dendriti obliqui con una frequenza di 60 hz.
La stimolazione di ogni neurone andrà avanti finché il neurone non riceverà un
input sui dendriti potenziati ossia finché non riceverà in input la codifica della
parola su cui è stato accordato.
25
Il nostro modello inoltre teorizza che, nel processo che conduce al ricordo di
parole apprese da una lista, si ha una stimolazione parallela di tutti i neuroni
coinvolti nella fase di apprendimento.
Fissato un tempo t0 avremo quindi N differenti neuroni, accordati su N
differenti parole da ricordare, stimolati contemporaneamente (figura 6).
Figura 6 rappresentazione grafica del nostro modello nell’istante di tempo
Sopra: 6 differenti neuroni della famiglia CA1 ognuno associato a una parola differente. Ogni neurone riceve un’n-pla di
potenziali di azione in una n-pla casuale di dendriti obliqui (codificanti una parola). i punti rossi rappresentano i
potenziali d’azione che arrivano sui dendriti potenziati i punti neri quelli che arrivano sui dendriti non potenziati.
Sotto: grafico del voltaggio nei soma dei neuroni nel momento della stimolazione
Al trascorrere del tempo avremo invece ciascun neurone, accordato su una
particolare parola, stimolato su n-ple di dendriti obliqui casuali codificanti
differenti parole (figura 7).
26
Figura 7 rappresentazione grafica di differenti stimolazioni di un singolo neurone al passare del tempo
Sopra: lo stesso neurone viene stimolato in istanti di tempo successivi tramite n-ple che codificano parole differenti
Sotto:grafici del voltaggio nel soma del neurone durante le differenti stimolazioni
3.7 Risultati
In [37] si è evidenziato come tramite questo modello si possano simulare dal
punto di vista qualitativo i dati riscontrati da Unsworth negli esperimenti di
delayed free recall.
Si è inoltre mostrato come il modello, utilizzando diversi neuroni di tipo CA1,
con diverse geometrie, riesca ad identificare un range di variabilità per il rumore
di membrana e per la dimensione della n-pla per i quali è possibile riprodurre
distribuzioni esponenziali cumulative come quelle riscontrate da Unsworth.
27
Inoltre le simulazioni hanno dimostrato che si è in grado di ottenere distribuzioni
molto simili a quelle calcolate come distribuzioni medie per alcuni particolari
categorie di esperimenti.
Ad esempio utilizzando il neurone con geometria geo9068802, che presenta 11
dendriti obliqui, codificando le parole tramite 7-ple e un valore medio di rumore
di 0,82 mv si sono ottenuti dati modellati da un’esponenziale cumulativa con
parametro λ=0,10 e con valore asintotico 3,37 entrambi valori molto vicini a
quelli ottenuti da Unswoth in media nei test fatti su persone con cattive capacità
mnemoniche nello studio di una lista di lunghezza 6 (figura 8) .
6
dati simulazioni
5
fitting
dist.Unsworth
Parole ricordate
4
3
2
1
0
0
10
20
30
40
50
Tempo
Figura 8: distribuzione esponenziale cumulativa ottenuta tramite simulazioni con parametri molto simili a quelli
riscontrati sperimentalmente da Unsworth
Questi dati mostrarono come il modello fosse in grado di produrre, almeno in
alcuni casi, dati dello stesso ordine di grandezza di quelli prodotti da Unsworth
28
sperimentalmente riuscendo a riprodurre distribuzioni rappresentative di un
insieme.
29
CAPITOLO 4
4.1 Introduzione:
In questo capitolo presenteremo l’evoluzione della tesi al fine di, tramite il
nostro modello, identificare le differenze fisiologiche sottostanti le diverse
capacità mnemoniche dei vari soggetti.
Presenteremo quindi i dati sperimentali fornitici da Unsworth, per poi passare
alle simulazioni svolte ed infine presenteremo i risultati ottenuti.
4.2 I dati sperimentali:
Come visto in precedenza e come mostrato in figura 9.a) e b) i dati sperimentali
ottenuti da Unsworth si distribuiscono secondo distribuzioni ben approssimabili
Fig9:a)dati sperimentali per 2 diverse categorie di esperimenti
b)esempi di dati sperimentali e esponenziale cumulativa che fitta al meglio
c)distribuzioni ottenute per le 6 categorie di esperimenti
30
a funzioni esponenziali cumulative i cui parametri , λ e A, variano in funzione
delle capacità mnemoniche del soggetto sottoposto all’esperimento e della
lunghezza della lista utilizzata nel test, rispettivamente da 0,01 a 0,3 e da 0,5 a
10 .
Inoltre in figura 9.c) si osserva come, raggruppando i dati sperimentali in
funzione della categoria di appartenenza (HighWMC o LowWMC) e della
lunghezza della lista utilizzata, si osservano, nello spazio parametrico (λ ,A),
delle distribuzioni difficilmente distinguibili perché in parte sovrapposte.
4.3 Trattamento dei dati sperimentali
Al fine di poter differenziare maggiormente le prestazioni nel test dei soggetti
con diverse capacità mnemoniche abbiamo effettuato un campionamento
selezionando i 10 soggetti che tra gli individui identificati da Unsworth come
HighWMC mostravano le maggiori capacità mnemoniche e i 10 soggetti che tra
i LowWMC mostravano le peggiori capacità mnemoniche.
Per
fare
ciò
abbiamo
ordinato
gli
individui
per
ogni
categoria
(HighWMC/LowWMC) e per ogni lunghezza della lista (6/9/12 parole) in
funzione del numero di parole che ricordavano in media, ottenendo quindi 6
classifiche 3 per gli individui con alte capacità mnemoniche e 3 per quelli con
scarse capacità mnemoniche.
Abbiamo quindi calcolato la media delle posizioni nelle 3 classifiche di
appartenenza di ogni soggetto e riordinato i due gruppi di individui in funzione
di questo valore.
Infine
abbiamo
selezionato
i
primi
10
individui
che
comparivano
nell’ordinamento degli individui con buone capacità mnemoniche e gli ultimi 10
che comparivano in quello degli individui con basse capacità mnemoniche.
31
Tramite questa metodologia abbiamo ottenuto i 10 soggetti che negli
esperimenti condotti da Unworth hanno mostrato la memoria migliore e i 10 che
hanno mostrato la memoria peggiore.
4.4 Le simulazioni:
Al fine di validare il modello proposto si sono definite delle simulazioni mirate
alla stimolazione di un neurone della famiglia CA1 tramite n-ple random di
potenziali d’azione sui dendriti obliqui.
Le nostre simulazioni sono state implementate nell’ambiente di sviluppo
Neuron, utilizzando per tutte le simulazioni il neurone di geometria
geoc91662.hoc che presenta 26 dendriti obliqui (figura 10).
Figura 10: rappresentazione 3d della ricostruzione ottenuta dalla geometria geoc91662
32
Il protocollo per la definizione delle simulazioni è il seguente: nella prima parte
del listato viene caratterizzato il neurone attraverso una serie di parametri che ne
stabiliscono le proprietà passive e la distribuzioni dei diversi canali ionici come
proposto in [31], successivamente viene assegnato un valore “n” corrispondente
alla dimensione del set di potenziali di azione che arrivano in input al neurone
(dimensione della codifica delle parole) e infine l’intensità del rumore di fondo
sul potenziale di membrana.
Viene quindi scelto in maniera random una n-pla di obliqui, rappresentante la
codifica della parola su cui il neurone è accordato, e vengono poste su di essi n
sinapsi eccitatorie, modellate tramite un doppio esponenziale (Exp2Syn in
Neuron). A queste sinapsi è stato dato un valore di conduttanza tale da
determinare dei potenziali d’azione locali sugli obliqui stessi mentre sugli altri
obliqui sono poste sinapsi con valore di conduttanza uguale a 0.
Il neurone viene quindi stimolato con al più 2700 input random (ogni input è una
n-pla di potenziali d’azione mandata sulle sinapsi presenti sugli obliqui)
corrispondenti al numero di input che un neurone CA1 riceve con una frequenza
di 60 hz in 45″.
In questo modo riusciamo a simulare tutto il periodo di 45″ proposto da
Unsworth nelle sue sperimentazioni, e concesso al soggetto esaminato per il
ricordo delle parole.
Infine, in funzione del verificarsi del potenziale d’azione sul soma, viene
interrotto il flusso di input e registrata la posizione dell’n-pla che ha determinato
il potenziale d’azione all’interno della serie di input. La posizione così calcolata
corrisponderà al tempo trascorso prima dell’insorgere del ricordo.
I dati così ottenuti sono stati quindi raccolti a gruppi di 6,9 e 12 in funzione delle
3 diverse tipologie di test presentate da Unsworth.
33
Si è quindi calcolato, per ognuno dei gruppi di dati così raccolti, il numero
medio di n-ple riconosciute, ossia il numero medio di parole ricordate, in
funzione del tempo.
Tramite questi raggruppamenti abbiamo simulato il funzionamento in parallelo
dei neuroni, nel meccanismo di recupero dell’informazione.
4.5 Simulazioni e dati sperimentali a confronto
Al fine di approssimare al meglio i dati sperimentali tramite il modello proposto
sono state condotte svariate simulazioni al variare della dimensione della n-pla
di codifica da 6 a 22 potenziali d’azione e con rumore di fondo da 1 a 1,3 mv.
Con questo range di rumore di fondo e di n-ple, abbiamo ottenuto distribuzioni
ben approssimabili a esponenziali cumulative.
Inoltre prendendo in considerazione i parametri delle esponenziali cumulative
che approssimano al meglio le simulazioni da noi svolte, si è riusciti a ricoprire
nello spazio parametrico (λ,A) la regione identificata dai fitting dei dati
sperimentali.
Dalla figura 11 si osservano le ottime approssimazioni dei dati sperimentali
Figura 11: distribuzioni ottenute tramite simulazioni per differenti valori di
rumore e taglia della n-pla di codifica ed dati sperimentali più vicini ad esse
34
ottenute per i diversi tipi di esperimenti e di individui e con valori di λ e A molto
diversi tra loro.
Inoltre è possibile osservare come esista una correlazione tra le proprietà
fisiologiche di cui abbiamo imposto la variazione nelle diverse simulazioni e i
parametri λ e A delle esponenziali cumulative associate alle simulazioni.
Infatti come è possibile osservare in figura 12 si ha un incremento dei valori di
entrembi i parametri all’aumentare della dimensione della n-pla di codifica
(figura12A),12B)) e un decremento degli stessi parametri all’aumentare del
rumore nel potenziale di membrana (figura 12C),12D)).
Figura12: sopra: valori di A e λ per diversi valori dell’n-pla di codifica
sotto: valori di A e λ per diversi valori del rumore di membrana
Inoltre associando ad ogni esponenziale cumulativa che modella al meglio i dati
sperimentali, degli individui da noi selezionati, l’esponenziale cumulativa con
parametri più simili ottenuta fittando i dati delle nostre simulazioni, abbiamo
ottenuto delle distribuzioni nello spazio (λ,A) molto simili a quelle sperimentali.
35
In figura 13 è possibile ad esempio osservare come le distribuzioni sperimentali
per i 10 individui con le più alte capacità mnemoniche negli esperimenti
condotti con liste di 12 parole e per i 10 individui con le più basse capacità
mnemoniche negli esperimenti con liste di 6 parole possano essere riprodotte in
modo molto fedele tramite distribuzioni esponenziali cumulative associate a
simulazioni prodotte dal nostro modello.
Figura 13:rappresentazione nello spazio (λ,A) delle esponenziali cumulative associate a dati sperimentali e esponenziali
cumulative relative alle simulazioni ad esse più vicine
4.6 Dallo spazio parametrico (λ,A)allo spazio delle proprietà fisiologiche (npla, rumore sul potenziale di membrana).
Nel paragrafo precedente si è mostrato come tramite il modello proposto si
riesca a riprodurre i dati sperimentali e inoltre si è in grado di costruire delle
distribuzioni nello spazio (λ,A) molto simili a quelle sperimentali per ogni
36
tipologia di esperimento e per ogni tipologia di individuo sottoposto
all’esperimento.
In questo paragrafo mostreremo come rappresentando le simulazioni, associate
alle diverse categorie di esperimenti, nello spazio delle proprietà fisiologiche
(n-pla, rumore sul potenziale di membrana) è possibile caratterizzare le 2
categorie di individui tramite questi parametri.
Nella figura 14 abbiamo rappresentato le simulazioni associate agli esperimenti
condotti su soggetti con alte capacità mnemoniche utilizzando liste composte da
12 parole e quelle associate agli esperimenti condotti su soggetti con basse
capacità mnemoniche utilizzando liste composte da 6 parole.
Figura 14:simulazioni associate a due differenti categorie di test rappresentate
nello spazio (n-pla, rumore sul potenziale di membrana)
È possibile osservare come le 2 distribuzioni interessino regioni
che si
sovrappongono solo in minima parte , suggerendo l’esistenza di regioni continue
37
nello spazio (n-pla, rumore sul potenziale di membrana) associate a regioni
continue nello spazio (λ,A).
Inoltre è possibile osservare in figura 15 come le simulazioni associate ai dati
sperimentali per i soggetti con alte capacità mnemoniche presentino in media
una taglia della n-pla di codifica e un rumore di fondo significativamente
maggiore di quello riscontrato per i soggetti con basse capacità mnemoniche.
Figura 15:media e deviazione standard della media della dimensione dell’n-pla e
del rumore sul potenziale di membrana per le 6 tipologie di esperimenti
Quest’ultimo dato lascia intravedere l’origine delle differenti capacità
mnemoniche negli individui associate a queste due variabili fisiologiche.
4.7 conclusioni
I dati presentati finora mostrano come tramite il modello proposto si è in grado
di riprodurre sia qualitativamente sia quantitativamente tutti i dati sperimentali
ottenuti da Unsworth nel processo di rievocazione libera.
Tramite questo contributo è stato inoltre possibile individuare, attraverso la
selezione dei 10 individui con le migliori capacità mnemoniche e dei 10
individui con le peggiori capacità mnemoniche, distribuzioni nello spazio
38
parametrico (λ,A) maggiormente caratterizzabili
in funzione dei diversi
esperimenti e delle 2 tipologie di individui sottoposti alla sperimentazione. A
partire da queste distribuzioni e da quelle ad esse associate, ricavate tramite le
simulazioni, siamo quindi riusciti a formulare l’ipotesi secondo cui una
maggiore capacità in termini di memoria di lavoro sia dovuta a un rumore di
membrana con maggiore intensità nei neuroni della famiglia CA1 e a una
codifica con n-ple di maggiore dimensione delle parole memorizzate.
A sostegno di questa ipotesi è possibile osservare come l’idea che i soggetti con
alte capacità mnemoniche codifichino con n-ple di dimensioni maggiori è
consistente con l’ipotesi di Unsworth e Engle [42] secondo cui le maggiori
capacità mnemoniche di alcuni soggetti dipendano dalla capacità di cercare la
parola da ricordare in un insieme più piccolo di parole.
Dal nostro lavoro risulta che in media i soggetti con alte capacità mnemoniche
utilizzino codifiche delle parole tramite 20-ple mentre i soggetti con basse
capacità mnemoniche utilizzino 14-ple.
Questa differenza nella codifica implica anche una differenza dimensionale del
dominio da cui vengono presi casualmente gli input.
Avremo infatti che per i soggetti con alte capacità mnemoniche il dominio sarà
 26 
composto da   = 230230 possibili 20-ple, ossia possibili parole, mentre per i
 20 
soggetti con basse capacità mnemoniche il numero di parole tra cui cercare sarà
 26 
dato dal numero di 14-ple selezionabili tra i 26 obliqui ossia   = 9657700.
 14 
Questo modello quindi oltre ad essere il primo modello neuro-computazionale
capace di riprodurre i dati sperimentali, relativi ad esperimenti di rievocazione
libera, svelando almeno in parte i meccanismi cerebrali relativi a questo
particolare processo, e apre anche la strada per un’interpretazione in termini
fisiologici di cosa sia la memoria di lavoro.
39
Suggerisce infatti come migliori capacità in termini di memoria di lavoro
possano essere associate a una rappresentazione più accurata a livello cerebrale
degli oggetti che compongono la realtà.
APPENDICE A
CODICE SIMULAZIONE
load_file("nrngui.hoc")
cvode_active(0)
a1=0.1
b1=0.71
a1max=0.1
b1max=0.71
rap=5
numaxon=1
numsoma=1
numbasal=58
numapical=78
numtrunk=57
cont=26 // number of obliques
last=22 // n-ple size
ns=26 // number of trunk comps with noise
sim4conf=102
double pin[cont]
double cond[cont]
double trunko[cont]
double dendo[cont]
double u2[last+3]
double u[last]
weight=80
xopen("geoc91662.hoc")
// geometry file
xopen("fixnseg.hoc")
Rm = 28000
RmDend = Rm/1
RmSoma = Rm
RmAx = Rm
Cm
= 1
CmSoma= Cm
CmAx = Cm
CmDend = Cm*1
RaAll= 150
RaSoma=150
RaAx = 50
Vrest = -65
dt = 0.1
gna = .025
AXONM = 5
gkdr = 0.01
celsius = 35.0
KMULT = 0.03
KMULTP = 0.03
ghd=0.00005
nash=0
objref g, b,c, stim, vbox,vecchio,pc, args, args2, r,ennupla
objref p, s[cont], rsyn[cont], nc[last], sref, blist[numtrunk],aplist,f[2*cont]
strdef dend, trunk
for i=0, numtrunk-1 {blist[i] = new Vector()}
args = new Vector()
args2 = new Vector()
aplist = new Vector(numapical)
forsec "axon" {insert pas e_pas=Vrest g_pas = 1/RmAx Ra=RaAx cm=CmAx}
forsec "soma" {insert pas e_pas=Vrest g_pas = 1/RmSoma Ra=RaSoma cm=CmSoma}
40
forsec "dendrite"{insert pas e_pas=Vrest g_pas = 1/RmDend Ra=RaAll cm=CmDend}
forsec "user5" {insert pas e_pas=Vrest g_pas = 1/RmDend Ra=RaAll cm=CmDend}
access soma
freq=50
geom_nseg()
tot=0
forall {tot=tot+nseg}
distance()
maxdist=0
forsec "user5" for(x) {if (distance(x)>maxdist) {maxdist=distance(x)}}
print "total # of segments (50Hz): ",tot, " max path distance: ", maxdist
//*********mapping bifurcations******************
for i=0, numapical-1 apical_dendrite[i] {
while (!issection("user5.*")) {
sref = new SectionRef()
access sref.parent
sprint(dend, secname())
}
for k=0, numtrunk-1 user5[k] {
sprint(trunk,secname())
x=strcmp(dend, trunk)
if (x==0) {blist[k].append(i)aplist.x[i]=k}
}
}
/*****************lettura da file********************/
vecchio = new File()
vecchio.ropen("obliqui91662.txt")
for i=0,cont-1 {
trunko[i]=vecchio.scanvar()
dendo[i]=vecchio.scanvar()
pin[i]=vecchio.scanvar()
cond[i]=vecchio.scanvar()
}
vecchio.close()
/******************** fine **********************/
tstop=30
for z=0, cont-1 {
s[z] = new NetStims(.5)
s[z].interval=0.2
s[z].number = 1
s[z].start=10
s[z].noise=0
s[z].seed(987651119)
rsyn[z] = new Exp2Syn(0.5)
rsyn[z].tau1 = 0.4
rsyn[z].tau2 = 1
rsyn.e=0
}
user5[13] {
stim= new IClamp(0)
stim.amp=0
stim.dur=tstop
stim.del=0
}
forsec "axon" {
insert nax gbar_nax=gna * AXONM
sh_nax=nash
insert kdr gkdrbar_kdr=gkdr
insert kap gkabar_kap = KMULTP*1
}
forsec "soma" {
insert hd ghdbar_hd=ghd
vhalfl_hd=-73
insert na3 ar_na3=1 sh_na3=nash gbar_na3=gna
insert kdr gkdrbar_kdr=gkdr
insert kap gkabar_kap = KMULTP
insert ds
}
for i=0, numbasal-1 dendrite[i] {
41
insert hd
insert
insert
insert
ghdbar_hd=ghd
vhalfl_hd=-73
na3 ar_na3=1 gbar_na3=gna sh_na3=nash
kdr gkdrbar_kdr=gkdr
kap gkabar_kap = KMULTP
}
forsec "user5" {
insert hd ghdbar_hd=ghd
insert na3 ar_na3=1 gbar_na3=gna sh_na3=nash
insert kdr gkdrbar_kdr=gkdr
insert kap gkabar_kap=0
insert kad gkabar_kad=0
for (x,0) {
xdist = distance(x)
ghdbar_hd(x) = ghd*(1+3*xdist/100)
if (xdist > 100){
vhalfl_hd=-81
gkabar_kad(x) = KMULT*(1+xdist/100)
} else {
vhalfl_hd=-73
gkabar_kap(x) = KMULTP*(1+xdist/100)
}
}
}
for i=0, numapical-1 apical_dendrite[i] {
insert hd
insert na3 ar_na3=1 gbar_na3=gna sh_na3=nash
insert kdr gkdrbar_kdr=gkdr
insert kap
insert kad
gkabar_kad = 1*user5[aplist.x[i]].gkabar_kad(1)
gkabar_kap = 1*user5[aplist.x[i]].gkabar_kap(1)
vhalfl_hd = user5[aplist.x[i]].vhalfl_hd
ghdbar_hd = user5[aplist.x[i]].ghdbar_hd(1)
}
proc init() {
t=0
forall {
v=Vrest
if (ismembrane("nax") || ismembrane("na3")) {ena=55}
if (ismembrane("kdr") || ismembrane("kap") || ismembrane("kad")) {ek=90}
if (ismembrane("hd") ) {ehd_hd=-30}
}
finitialize(Vrest)
fcurrent()
forall {
for (x) {
if(ismembrane("na3")||ismembrane("nax")){
e_pas(x)=v(x)+(ina(x)+ik(x))/g_pas(x)
}
if (ismembrane("hd")) {e_pas(x)=e_pas(x)+i_hd(x)/g_pas(x)}
}
}
cvode.re_init()
cvode.event(tstop)
access soma
flag=0
}
proc advance() {
fadvance()
if (vmax_ds(.5)>0) {t=tstop flag=1}
//g.plot(t)
//g.flush()
//p.flush()
42
doNotify()
}
func superrun() {
local id, numprove, c, k, seme1, seme2, seme3
a1=$o2.x[0]
b1=$o2.x[1]
stim.amp=$o2.x[2]
k=$3
c=$4
seme1=(k*sim4conf+c)*31530
seme2=(k*sim4conf+c)*22210
seme3=(k*sim4conf+c)*18230
print "seme1", seme1
print "seme2", seme2
print "seme3", seme3
for kk=0, ns user5[kk] {
f[kk] = new Gfluct2(0.5)
f[kk].g_e0 = a1
f[kk].g_i0 = b1
f[kk].std_e = a1/rap
f[kk].std_i = b1/rap
f[kk].new_seed(seme1)
print " noise #",kk, " at ",secname()
}
print k,c
objref ennupla
numprove=0
id = hoc_ac_
ennupla= new Vector()
flag=0
// definiamo ennupla
for c=0, cont-1 {
ennupla.append(c)
}
aux=cont
r= new Random()
r.MCellRan4(seme3)
for c=0, last-1 {
ind=r.discunif(0, aux-1)
cond[ennupla.x[ind]]=80
aux=aux-1
print ennupla.x(ind)
ennupla.remove(ind)
}
print "\n"
for c=0, cont-last-1 {
cond[ennupla.x(c)]=0
print ennupla.x(c)
}
ennupla.resize(0)
r= new Random(seme2)
r.MCellRan4(seme2)
while(flag==0){
numprove=numprove+1
for c=0, cont-1 {
ennupla.append(c)
}
aux=cont
for c=0, last-1 {
ind=r.discunif(0, aux-1)
u[c]=ennupla.x[ind]
u2[c]=dendo[u[c]]
nc[c] = new NetCon(s[u[c]],rsyn[u[c]],0,0,cond[u[c]]*1.e-3)
apical_dendrite[u2[c]] rsyn[u[c]].loc(0.5)
ennupla.remove(ind)
43
aux=aux-1
}
ennupla.resize(0)
run()
if (flag==1) { print "ha sparato dopo",numprove,"prove" spikec=1}
if(numprove>3600){print "piu di 3600 prove" flag=1 spikec=0}
}
pc.post(id, $o2,numprove,seme1,seme2,seme3)
return id
}
pc = new ParallelContext()
pc.runworker()
for yy=0, last-1 {u[yy]=0}
order=0
conto=0
print "Begin Simulation"
print "Contesto = ",stim.amp
objref aa1, bb1, aamp
aa1 = new Vector()
bb1 = new Vector()
aamp = new Vector()
aa1.append(0.095)
bb1.append(0.095)
contex = 0.3
proc loop() { local k, first, ind, c
k=$1
c=$2
args.resize(0)
args.append(aa1.x[nsim]*a1max)
args.append(bb1.x[nsim]*b1max)
args.append(contex)
pc.submit("superrun", order, args,k,c)
order=order+1
}
for nsim=0, aa1.size()-1 {
for z=1,sim4conf{
loop(nsim,z)
}
}
objref outfile, outfile2
outfile = new File()
outfile2 = new File()
strdef name, name2
total=0
while ((id = pc.working) != 0) {
pc.take(id)
args2 = pc.upkvec
m = pc.upkscalar
seme1=pc.upkscalar
seme2=pc.upkscalar
seme3=pc.upkscalar
total = total +1
sprint(name,"le%dple-%dobl-%gecc-%gini%d.txt",last,cont,args2.x[0]/a1max,args2.x[1]/b1max,sim4conf)
sprint(name2,"le%dple-%dobl-%gecc-%gini-solotempi%d.txt",last,cont,args2.x[0]/a1max,args2.x[1]/b1max,sim4conf)
outfile.aopen(name)
outfile.printf(" %d configurazioni ",m)
args2.printf(outfile, " %g ")
outfile.printf(" seme r seme e semel %d %d %d",seme1,seme2,seme3)
outfile.close()
outfile2.aopen(name2)
outfile2.printf(" %d
%d \n",m,seme1)
outfile2.close()
}
pc.done
44
BIBLIOGRAFIA
1) Ackerman, P. L., Beier, M. E., & Boyle, M. O. Working memory and intelligence: The same or
different constructs? Psychological Bulletin 131: 30–60,2005.
2) Andersen P, Morris R, Amaral D, Bliss T, O’Keefe J. Historical perspective: proposed
functions, biological characteristics, and neurobiological models of the hippocampus. In:
Andersen P, Morris R, Amaral D, Bliss T, O’Keefe J, editors. The Hippocampus Book. New
York: Oxford University Press, 2006.
3) Baddeley, A. D. Human Memory. Theory and Practice. Hove, Erlbaum.1990
4) Baddeley, A. D. Exploring the central executive. Quarterly Journal of Experimental
Psychology, 49A:5-28,1996
5) Baddeley, A. D. The episodic buffer: A new component of working memory? Trends in
Cognitive Sciences 4: 417-423,2000
6) Baddeley, A. D., Hitch, G. Working memory. In G. A. Bower (Ed), Recent Advances in
Learning and Motivation (47-90). New York: Academic Press,1974.
7) Baddeley A. D., Logie, R. H. Working memory: The multiple-component model. In A. Miyake
& P. Shah. (Eds), Models of Working Memory (pp. 28-61). Cambridge: Cambridge University
Press. 1999
8) Bannister NJ, Larkman AU. Dendritic morphology of CA1 pyramidal neurones from the rat
hippocampus. II. Spine distributions. J Comp Neurol 360:161–171, 1995.
9) Conway, A. R. A., Cowan, N., Bunting, M. F., Therriault, D. J., & Minkoff, S. R. B. A latent
variable analysis of working memory capacity,short-term memory capacity, processing
speed, and general fluid intelligence.Intelligence 30: 163–183.2002.
10) Cornoldi, C. La memoria di lavoro visuo-spaziale. In Marucci F.S. (Ed), Le immagini mentali .
La Nuova Italia Scientifica,145-180,1995
11) Daneman, M., Carpenter, P. A. Individual differences in working memory and reading.
Journal of Verbal Learning and Verbal Behavior, 19, 450–466, 1980.
12) Daneman, M., Green, I. Individual differences in comprehending and producing words in
context. Journal of Memory and Languag, 25:1-18,1986.
13) Engle, R. W., Tuholski, S. W., Laughlin, J. E., & Conway, A. R. A. Working memory, shortterm memory and general fluid intelligence: A latent-variable approach. Journal of
Experimental Psychology: General 128: 309–331.1999
14) Gasparini S, Losonczy A, Chen X, Johnston D, Magee JC. Associative pairing enhances action
potential back-propagation in radial oblique branches of CA1 pyramidal neurons. J Physiol
580:787–800, 2007.
15) Gasparini, S., Migliore, M., Magee, J. C. On the initiation and propagation of dendritic spikes
in CA1 pyramidal neurons. The Journal of Neuroscience, 24, 11046–11056, 2004.
16) Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput 9:1179–
1209,1997.
45
17) Ishizuka N, Cowan WM, Amaral DG. A quantitative analysis of the dendritic organization of
pyramidal cells in the rat hippocampus. J Comp Neurol. 6;362(1):17-45, 1997.
18) Johnston D, Amaral DG. Hippocampus. In: Shepherd GM, editor. The Synaptic Organization
of the Brain. New York: OxfordUniversity Press. Chapter 11, 2003.
19) Kane, M. J., Hambrick, D. Z., Tuholski, S. W., Wilhelm, O., Payne, T. W., & Engle, R. W. The
generality of working-memory capacity: A latent-variable approach to verbal and visuospatial memory span and reasoning. Journal of Experimental Psychology: General 133: 189–
217.2004
20) Kyllonen, P. C., & Christal, R. E. Reasoning ability is (little more than) working-memory
capacity? Intelligence,14: 389–433.1990
21) Kyllonene P.C.,Stephens D.L.Cognitive abilities as the determinant of success in acquiring
logic skillslearning and individual differences 2:129-160, 1990;
22) Logie, R. H. Visuo-spatial short-term memory: Visual working memory or visual buffer? In C.
Cornoldi & M. McDaniel (Eds), Imagery and Cognition (pp. 77-102). New York:SpringerVerlag,1991.
23) Logie, R. H.. Visuo-spatial Working Memory. Hove, UK: Lawrence Erlbaum Associates
Ltd.,1995
24) Logie, R. H. Visuo-spatial processes in working memory. Quarterly Journal of Experimental
Psychology, 38A: 229-247,1986.
25) Logie, R. H., Della Sala, S., Wynn, V., & Baddeley, A. D. Visual similarity effects in immediate
verbal serial recall. The Quarterly Journal of Experimental Psychology, 53A, 626646, 2000.
26) Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1
pyramidal neurons. Neuron 50: 291–307, 2006.
27) Miyake, A., & Shah, P. Toward unified theories of working memory: Emerging general
consensus, unresolved theoretical issues, and future research directions. In A. Miyake & P.
Shah (Eds), Models of Working Memory: Mechanisms of Active Maintenance and Executive
Control (pp. 442-481). New York: Cambridge University Press,1999.
28) Megias M, Emri Z, Freund TF, Gulyas AI. Total number and distribution of inhibitory and
excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience 102:527–540, 2001.
29) Miller G.A. The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for
Processing Information.The Psychological Review 63: 81-97,1956.
30) Migliore M, Ferrante M, Ascoli GA. Signal propagation in oblique dendrites of CA1 pyramidal
cells. J Neurophysiol 94: 4145–4155, 2005.
31) Migliore M, Novara G, Tegolo D. Single neuron binding properties and the magical number
7. HIPPOCAMPUS 18:1122–1130, 2008.
32) Migliore M, Shepherd GM. Emerging rules for the distributions of active dendritic
conductances. Nature Rev Neurosci 3: 362–370,2002.
33) Morris R. Theories of hippocampal function. In: Andersen P, Morris R, Amaral D, Bliss T,
O’Keefe J, editors. The Hippocampus Book. New York: Oxford University Press. Chapter 13,
2006.
34) Quiroga RQ, Reddy L, Kreiman G, Koch C, Fried I. Invariant visual representation by single
neurons in the human brain. Nature 435:1102–1107, 2005.
35) Salway, A. F. S., & Logie, R. H. Visuospatial working memory, movement control and
executive demands. British Journal of Psychology, 86, 253-269.1995
36) Shute, Valerie J. Who is likely to acquire programming skills?Journal of Educational
Computing Research, Vol 7(1): 1-24,1991.
37) Spera ,E. Modello computazionale dei possibili processi cerebrali alla base del
riconoscimento di oggetti in una lista.2010
38) Squire LR, Stark CEL, Clark RE. The medial temporal lobe. Ann Rev Neurosci 27:279–306,
2004.
46
39) Turner, M. L., & Engle, R. W. Is working memory capacity task dependent? Journal of
Memory and Language, 28: 127–154,1989
40) Unswoth. Individual differences in working memory capacity and episodic retrieval:
examining the dynamics of delayed and continuous distractor free recall. Journal of
Experimental Psychology: Learning, Memory, and Cognition, Vol. 33, No. 6, 1020–1034, 2007.
41) Unsworth, N., & Engle, R. W. Working memory capacity and fluid abilities: Examining the
correlation between operation span and raven.Intelligence, 33: 67–81,2005.
42) Unsworth, N., & Engle, R. W. The nature of individual differences in working memory
capacity: Active maintenance in primary memory and controlled search from secondary
memory. Psychological Review, 114, 104–132, 2007.
47