Nome file d:\scuola\corsi\corso fisica\meccanica\moti periodici\moto armonico.doc
Elaborato il 22/11/2002 alle ore 5.48 ,
salvato il 22/11/02 17.48
Creato il 20/11/2002 7.23
Dimensione file: 48640 byte
stampato il 22/11/2002 5.48
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
Moto armonico
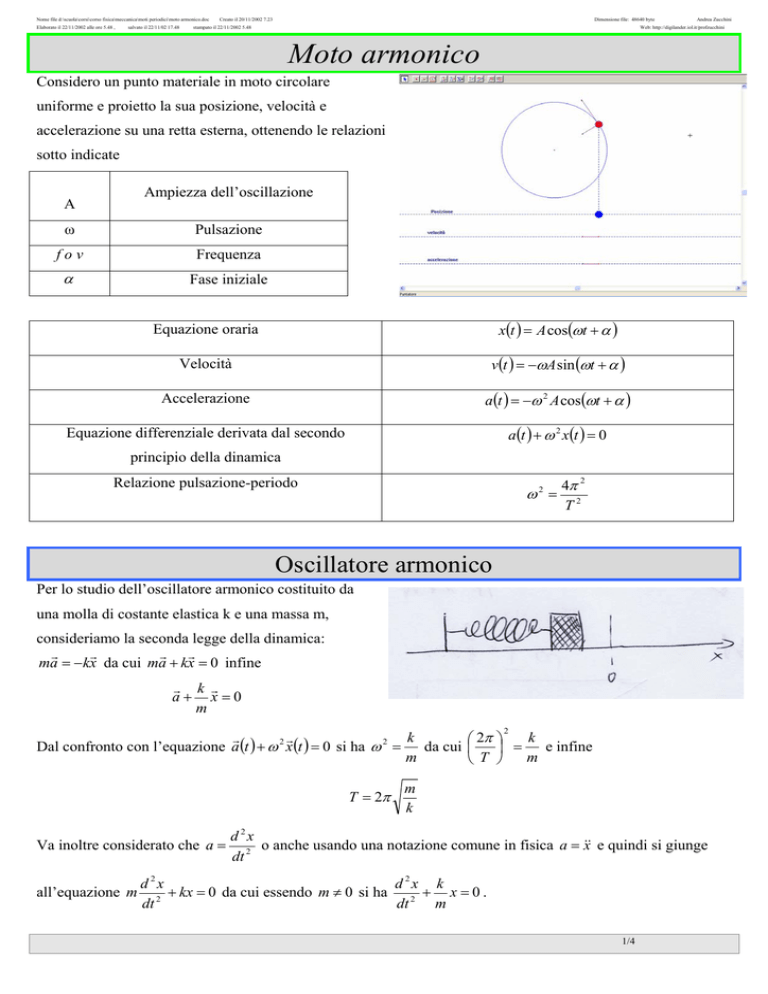
Considero un punto materiale in moto circolare
uniforme e proietto la sua posizione, velocità e
accelerazione su una retta esterna, ottenendo le relazioni
sotto indicate
A
Ampiezza dell’oscillazione
ω
Pulsazione
foν
Frequenza
α
Fase iniziale
Equazione oraria
x(t ) = A cos(ωt + α )
Velocità
v(t ) = −ωA sin (ωt + α )
Accelerazione
a (t ) = −ω 2 A cos(ωt + α )
Equazione differenziale derivata dal secondo
a (t ) + ω 2 x(t ) = 0
principio della dinamica
Relazione pulsazione-periodo
ω2 =
4π 2
T2
Oscillatore armonico
Per lo studio dell’oscillatore armonico costituito da
una molla di costante elastica k e una massa m,
consideriamo la seconda legge della dinamica:
r
r
r r
ma = − kx da cui ma + kx = 0 infine
r k r
a+ x =0
m
2
r
r
k
k
2π
Dal confronto con l’equazione a (t ) + ω 2 x (t ) = 0 si ha ω 2 =
da cui
e infine
=
m
m
T
T = 2π
m
k
d 2x
Va inoltre considerato che a = 2 o anche usando una notazione comune in fisica a = &x& e quindi si giunge
dt
d 2x
d 2x k
all’equazione m 2 + kx = 0 da cui essendo m ≠ 0 si ha 2 + x = 0 .
dt
dt
m
1/4
Nome file d:\scuola\corsi\corso fisica\meccanica\moti periodici\moto armonico.doc
Elaborato il 22/11/2002 alle ore 5.48 ,
Ponendo ω 2 =
salvato il 22/11/02 17.48
Creato il 20/11/2002 7.23
Dimensione file: 48640 byte
stampato il 22/11/2002 5.48
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
k
d 2x
ottengo l’equazione differenziale 2 + ω 2 x = 0 .
m
dt
Esistono tecniche di ricerca delle soluzioni di particolari equazioni differenziali ma in questo caso andremo alla
ricerca di una soluzione dell’equazione facendo una ipotesi iniziale: l’equazione oraria del moto è della forma
x(t ) = A cos(ωt + α ) infatti
dx
d 2x
= − Aω sin (ωt + α ) e 2 = − Aω 2 cos(ωt + α ) = −ω 2 x(t ) e sostituendo
dt
dt
nell’equazione originale si ha − ω 2 x + ω 2 x = 0 .
Calcolando l’energia totale si devono tenere in considerazione due contributi:
2
1
1 dx
1
1
2
Energia cinetica : Ec = mv 2 = m = m[Aω sin (ωt + α )] = mA2ω 2 sin 2 (ωt + α )
2
2 dt
2
2
1
1
1
1
2
Energia potenziale : E p = kx 2 = k [ A cos(ωt + α )] = kA2 cos 2 (ωt + α ) = mω 2 A 2 cos 2 (ωt + α )
2
2
2
2
1
1
L’energia totale sarà Etot = Ec + E p = mA2ω 2 sin 2 (ωt + α ) + mω 2 A 2 cos 2 (ωt + α )
2
2
da cui si ha
1
1
Etot = mA2ω 2 sin 2 (ωt + α ) + cos 2 (ωt + α ) = mA2ω 2
14444244443
2
2
1
L’energia totale dell’oscillatore armonico dipende dalla massa in oscillazione, dall’ampiezza e dalla pulsazione.
Pendolo semplice
Considero una massa m attaccata ad un filo di lunghezza
l, privo di massa e inestensibile.
La posizione del pendolo è univocamente individuata
dall’angolo ϑ misurato a partire dalla verticale e
assunto positivo quando la massa si trova a destra
(misura in senso antiorario partendo dalla verticale).
Sulla massa agiranno le forze peso e di tensione del filo
e per il movimento l’unica forza utile sarà la
componente perpendicolare al filo.
Dalla figura risulta F = −mg sin (ϑ )
Avrò allora − mg sin (ϑ ) = ma da cui ma + mg sin (ϑ ) = 0
da cui infine a + g sin(ϑ ) = 0 .
Quando l’angolo ϑ è piccolo si avrà a + gϑ = 0 da cui infine essendo ϑ =
s
avrò
l
d 2s g
g
a + s = 0 o anche 2 + s = 0
dt
l
l
2/4
Nome file d:\scuola\corsi\corso fisica\meccanica\moti periodici\moto armonico.doc
Elaborato il 22/11/2002 alle ore 5.48 ,
salvato il 22/11/02 17.48
Creato il 20/11/2002 7.23
Dimensione file: 48640 byte
stampato il 22/11/2002 5.48
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
2
g
2π
da cui avremo ω 2 =
= e quindi
l
T
T = 2π
l
g
g
La forza che agisce è ancora una volta (almeno in prima approssimazione) F = − m s , proporzionale allo
l
spostamento misurato sull’arco percorso dal pendolo.
Circuito LC
Esistono molte situazioni fisiche riconducibili al caso dell’oscillatore armonico;
vediamo come esempio il circuito LC ovvero un circuito elettronico costituito da due
dispositivi detti bobina (o meglio induttanza) e condensatore.
Le tensioni (i volt) ai capi dei due dispositivi saranno VL = L
avremo
∆i
i
e ∆VC = ∆t da cui
∆t
C
∆VC
∆VL
∆2 i
i
=L 2 e
= .
∆t
∆t
C
∆t
3/4
Nome file d:\scuola\corsi\corso fisica\meccanica\moti periodici\moto armonico.doc
Elaborato il 22/11/2002 alle ore 5.48 ,
salvato il 22/11/02 17.48
Creato il 20/11/2002 7.23
Dimensione file: 48640 byte
stampato il 22/11/2002 5.48
Dato che le tensioni in gioco dovranno essere istantaneamente uguali, avrò
L
Andrea Zucchini
Web: http://digilander.iol.it/profzucchini
∆VL ∆VC
+
= 0 da cui ricavo
∆t
∆t
∆2 i i
+ = 0 e infine
∆t 2 C
1
∆2 i
+
i=0
2
∆t
LC
Mettiamola a confronto con le analoghe
d 2x k
+ x = 0 oscillatore armonico semplice
dt 2 m
d 2s g
+ s = 0 pendolo
dt 2 l
Le equazioni sono formalmente uguali e hanno la stessa soluzione del tipo
i (t ) = i0 cos(ωt + α )
e il periodo sarà
T = 2π LC
In conclusione possiamo dire che ogni volta che studiando un fenomeno
fisico si presenta una equazione del tipo
∆2 x
+K⋅x =0
∆t 2
nella variabile x(t ) dipendente dal tempo e con K costante si ha un
fenomeno di tipo armonico e la dipendenza della variabile x dal tempo è
del tipo
x(t ) = A cos(ωt + α )
4/4











